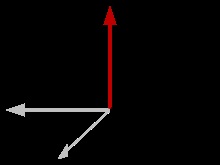
După inversiune, doi vectori își schimbă semnul, dar produsul lor vectorial rămâne neschimbat.
vector axial (axial liniei centrale Engl ..) sau pseudo - cantitatea ale cărei componente sunt transformate cu vectorul rotației sistemului de coordonate, dar se schimba semnul este opus comportamentului componentelor vectorului în orice inversare (circulație semn) coordonează. Ie pseudo inversează menținând valoarea absolută (este înmulțită cu un minus) la orice inversare a sistemului de coordonate.
Pentru a sublinia diferența vectorului prezent, ale cărui coordonate sunt întotdeauna transformate în același mod ca și coordonatele vectorului de deplasare, vectorul real este numit vectorul adevărat sau polar.
Cel mai simplu exemplu al unui vector axial într-un spațiu tridimensional este produsul vector al a doi vectori polari, de exemplu, în mecanică, momentul unghiular # x00D7; . în spațiul tridimensional - un curent axial.
Informații de bază
Când transformarea de coordonate de coordonate vectorul axial obținut prin înmulțirea unui factor suplimentar (-1) în comparație cu adevărata transformare de coordonate (altfel denumit polare) vectori, în cazul în care baza se schimbă orientarea (de exemplu, în cazul în care baza este supusă reflexie). Acest lucru, alături de un pseudoscalar. caz special al unui pseudotensor. Pseudovectorul reprezentat grafic cu această schimbare a coordonatelor inversează direcția sa.
- Geometria reprezentare aplicare pseudovec- cel mai utilizat pe scară largă poate fi cu ajutorul tridimensional de rotație infinit de mici. Probabil (?), Vectorul Termenul axială este tocmai aici, deoarece pseudo definește o axă de pivotare (direcția), dar numai până la un factor de (± 1), cu direcția de rotație a alegerii arbitrare condiționată asociat bazei drept, spre deosebire de adevărat ( polar) reprezentând un segment direcționat (sau transport paralel) este complet definit și determinat în mod unic de punctele de început și de sfârșit.
Modul obișnuit de a genera pseudovectors pseudovectorial această operațiune, cel mai frecvent, dacă nu singurul utilizat în mod obișnuit în cazul tridimensional este produsul vectorial (așa cum se obișnuiește în notația de coordonate include Levi-Civita pseudo) operație și care conține produsul vectorial (de exemplu, rotor etc. .) sau un număr impar de ele. operațiune Pseudovector generează adevărate de vectori și scalari pseudovectors și pseudoscalars.
Astfel, atunci când vectorul adevărat este înmulțit cu un vector adevărat, adevăratul scalar este obținut în produsul scalar și pseudovectorul în produsul vectorial. Atunci când vectorul adevărat este înmulțit cu un pseudovector, se obține pseudoscalar în produsul scalar și produsul vector în produsul vectorial. Atunci când se înmulțesc doi pseudovectori, se obțin adevăratul scalar și pseudovector.
Teoriile fizice, cu excepția celor în care există un distinct și observabile în principiu pseudovectors spațiu de simetrie în oglindă poate fi prezentă în valorile intermediare, dar în final observate - Multiplicatorii (-1) la reflectarea în oglindă a coordonatelor trebuie eliminate, reuniți în lucrările chiar număr de ori (chiar și numărul de pseudovector pseudoscalari + + alți factori pseudotensorial).
- De exemplu, în electrodinamica clasică, inducerea unui câmp magnetic este un pseudovector, deoarece este generat de o operație de pseudovector, de exemplu # x00D7; în legea Bio-Savar. dar această valoare (pseudovector) este determinată în principiu până la un multiplicator condițional care poate fi ales +1 sau -1. Cu toate acestea, valoarea observată efectiv - accelerarea unei încărcări sub acțiunea unui câmp magnetic - în calculul său conține o altă operație pseudovector # x00D7; în expresia forței Lorentz. care dă un multiplicator condițional mai mult ± 1 egal cu primul, în răspuns, arbitraritatea dispare, deoarece produsul ± 1 (± 1) dă doar 1.
- În mecanică, cel mai frecvent întâlnit pseudovector este vectorul vitezei unghiulare și asociat cu acesta (de exemplu, un moment unghiular). Vectorul real de viteză este obținut de la pseudovectorul vitezei unghiulare # x03C9; funcționarea pseudovectorului # x03C9; # x00D7; .