Alocarea dinamică a memoriei
Funcția p = select (N) returnează un pointer la un obiect de memorie cu lungimea N,
În C, p = new (N) (un tip pointer indefinit).
1) Tastați indicatorul.
În limbile de scriere stricte, int * p și char * g nu sunt echivalente => este necesară o conversie de tip.
2) Eliberați memoria alocată
· Mecanism explicit (programator) - funcția de distrugere (p);
· Nu există un mecanism explicit (OS) - este distrus atunci când nu există referințe la obiect, este posibil să se pună în aplicare prin intermediul temporizatorului, la finalizarea programelor, în caz de depășire.
3) Problema obiectelor agățate (atunci când un obiect dinamic se referă la un alt obiect dinamic)
În memorie există obiecte fără referințe. Distrugând acest obiect, puteți pierde referințe la toate subiectele sale.
4) problema agățării pointerilor (rămân referințe la obiecte distruse);
5) Fragmentarea memoriei
Distruge p3 și p5 - noul obiect are suficientă memorie, dar nu va mai fi singur
Reguli de lucru cu memorie dinamică în prezența unor mecanisme explicite de distrugere:
1) Nu permiteți prezența obiectelor agățate. Pentru a face acest lucru, trebuie mai întâi să distrugeți toate obiectele atașate.
2) Nu permiteți legăturile suspendate, adică după distrugerea obiectului, ștergerea și referința la acesta - p = NULL.
3) Minimizați fragmentarea. Pentru a face acest lucru, trebuie să distrugeți obiectele în ordinea inversă a creării lor: p5 - p4 - p3.
Implementarea mecanismului de memorie dinamică în C:
1) Alocarea memoriei dinamice prin funcția void * malloc (size_t size).
De exemplu, dacă aveți nevoie de 10 elemente dintr-o matrice, atunci:
Dimensiunea dimensiunii size_t necesară poate fi mai mare decât este necesar (pentru aliniere)
2) Funcția void * calloc (size_t num, size_t size);
toate valorile din memoria recepționată sunt zero.
3) void free (void * p)
pointerul indică blocul de memorie capturat anterior cu operațiunile malloc, calloc, realloc, adică numărul de octeți care trebuie eliberați = numărul de octeți recepționați în timpul capturării
conversia int în void ((void *) A);
4) Funcția void * realloc (void * p, size_t new size)
Modifică dimensiunea blocului de memorie capturat anterior, p - un indicator la începutul blocului, dimensiunea - mărime în octeți. Blocul poate fi mutat în memorie când dimensiunea se modifică.
Copaci. DEFINIȚII, CLASIFICARE, METODE DE PREZENTARE.
Un arbore cu o bază tip T este:
1) Fie un copac gol
2) Sau un vârf de tip T cu un număr finit de arbori asociați cu un tip de bază T (substraturi).
(Un arbore la care se face referire printr-un vârf - un substrat)
Vârful la care se referă celălalt vertex este descendentul său. Vertexul invers este strămoșul.
Un vârf care nu are descendenți este o frunză de copac.
Dacă numărăm vârfurile astfel încât fiecare copil următor să fie cu un nivel superior, atunci vârful la nivelul 0 este rădăcina copacului.
Un vârf care nu este o frunză este un vertex interior.
Nivelul oricărui vârf este adâncimea (înălțimea). iar adâncimea copacului în sine este adâncimea maximă a tuturor vârfurilor.
Numărul descendenților imediați ai unui vârf se numește gradul unui vârf dat, gradul unui arbore fiind maximumul tuturor gradelor posibile.
Numărul de ramuri (marginile) care trebuie să treacă de la rădăcină la vertexul x se numește lungimea căii la x (rădăcina are calea 0).
Lungimea traseului întregului copac (lungimea căii interioare) este suma lungimilor căii către toate vârfurile.
Lungimea medie a căii este determinată de formula :.
Un copac este numit comandat. dacă toate ramurile care provin de la orice vârf sunt, de asemenea, ordonate.
Arborii comandați de gradul doi sunt numiți arbori binari.
Copacii de gradul n (mai mare de 2) se numesc ramificații puternice.
Copacii care au o înălțime minimă sunt numiți perfect echilibrați (numărul de vârfuri din substraturile din stânga și din dreapta diferă cu nu mai mult de 1 - condiția pentru toate vârfurile).
Expresia unor astfel de structuri recursive necesită utilizarea unor referințe.
Există multe moduri diferite de reprezentare a copacilor (de exemplu, un copac binar):
1) Reprezentarea pe listă a arborilor binari se bazează pe elementele corespunzătoare nodurilor copacului. Fiecare element are un câmp de date și două câmpuri de pointer. Un pointer este utilizat pentru a lega elementul de copilul drept, iar celălalt la stânga. Frunzele au indicii goale de descendenți. Cu acest mod de a reprezenta copacul, ar trebui să păstrați întotdeauna un pointer la nodul care este rădăcina copacului.
Puteți observa că acest mod de reprezentare are o asemănare cu listele liniare simple. Și această asemănare nu este accidentală. De fapt, modalitatea considerată de a reprezenta un arbore binar este un fel de multisesiune formată dintr-o combinație de seturi de liste liniare. Fiecare listă liniară combină nodurile care intră în calea de la rădăcina copacului la una din frunze.
struct binary_tree * stânga;
struct binary_tree * dreapta;
Apoi copacul gol este pur și simplu determinat prin setarea variabilei Root la zero:
Root = NULL;
2) În forma unei matrice, arborele binar complet este cel mai ușor reprezentat, deoarece are întotdeauna un număr strict definit de noduri pe fiecare nivel. Vârfurile pot fi numerotate de la stânga la dreapta în mod succesiv prin nivele și pot utiliza aceste numere ca indici într-o matrice unidimensională.
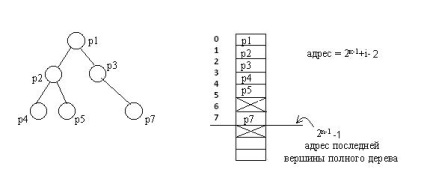
Dacă numărul de nivele ale copacului nu se schimbă semnificativ în timpul procesării, atunci acest mod de reprezentare a unui arbore binar complet va fi mult mai economic decât orice structură de listă.
Principalul dezavantaj al modului considerat de a reprezenta un arbore binar este că structura de date este statică. Dimensiunea matricei este aleasă pe baza numărului maxim posibil de nivele ale arborelui binar. Și cu cât copacul este mai puțin complet, cu atât este mai puțin folosită memoria.
STÂNZURI BINARE, OPERAȚII.
Binar copac - un set finit de elemente (noduri), care este fie gol sau constă dintr-o rădăcină cu două subramificații binare separate, sunt numite subramificație stânga și dreapta rădăcinii.
Pentru a construi un arbore binar cu n noduri având o înălțime minimă, se utilizează următoarele reguli:
0) Dacă n = 0, atunci sfârșitul;
1) Construiți vârful
2) Construiți un substrat de stânga cu vârfuri;
3) Construiește un substrat drept cu vârfuri.
Operațiuni cu copaci binari:
· Bypass prefix - vârf, stânga, dreapta (+ ab):
prefix_walk (struct binary_tree * t)
· Bypass infix - stânga, vârf, dreapta (a + b);
· Postfix - stânga, dreapta, vârf (ab +);
Dacă utilizați în scopul de a găsi elementele de date privind valoarea cheii unice folosite binar de căutare de căutare copac copac - toate nodurile din subarborele din dreapta> x (sus), toate nodurile din subarborele stâng Elementele N pot fi organizate într-un arbore binar cu o înălțime nu mai mare decât log2 (N). prin urmare, pentru a căuta printre elementele N, este posibil să nu se ia mai mult decât comparațiile log2 (N) dacă copacul este perfect echilibrat. Rezultă că un arbore este o structură mai potrivită pentru organizarea unei căutări decât, de exemplu, o listă liniară.Articole similare