77. A trebuit deja să construim quadrangles (paragraful 50). Acum extindem această construcție. Lăsați 4 puncte: A, B, C și D [cher. 84 (I)]; construim toate liniile directe posibile care leagă aceste patru puncte în perechi - presupunem că nici 3 dintre aceste puncte nu sunt situate pe aceeași linie. Astfel de linii pot construi toate cele 6 (de la fiecare punct la celelalte trei sunt 3 linii, ca puncte 4, directe 3 * 4 = 12, dar fiecare linie totală este considerată a fi de două ori mai mare, de exemplu direct AC :. Odată ce am considerat atingerea de la A la C și, uneori, de la C la A, linii diferite trebuie să fie (4 * 3) / 2 = 6). Figura rezultată constă din 4 puncte și 6 linii care le conectează în perechi - se numește un quadrangle complet. Fiecare dintre aceste patru puncte este numit punctul său vertex. Și fiecare linie dreaptă care intră în ea este partea lui. un plin 4-gon are 4 noduri și 6 laturi.
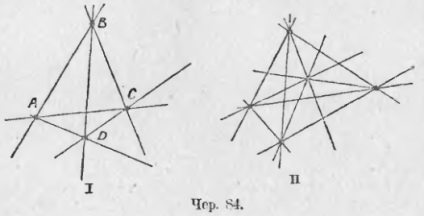
Dacă luăm 5 puncte (barul 84 - II), astfel că nici 3 dintre ei nu se află pe o singură linie, iar noi îi conectăm în perechi, obținem un 5-gon plin; are 5 vârfuri și 10 laturi. Un plin 6-gon are 6 vârfuri și 15 laturi și așa mai departe.
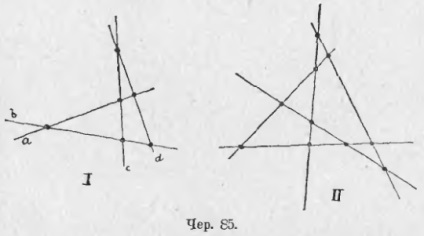
Dimpotrivă, este posibil să construim 4 linii drepte a, b, c și d (85 - I), astfel încât niciunul dintre ei să nu treacă printr-un punct și să găsească punctele lor de intersecție. Să presupunem că nu există perechi de linii paralele între liniile a, b, c și d; atunci fiecare linie cu cele trei intersecte rămase la trei puncte și întregul punct de intersecție este 3 * 4 = 12, dar aici fiecare punct a fost numărat de 2 ori: o dată, de exemplu, de la intersecția liniei a cu linia b, iar celălalt de la intersecția liniei b cu linia a; prin urmare, numărul de puncte diferite de intersecție trebuie să fie 4 * 3/2 = 6. Figura rezultată, formată din 4 linii drepte și 6 puncte din intersecția lor, se numește patrulateră completă; fiecare linie este numită partea ei și fiecare punct este vârful ei. Quadrilateral are 4 laturi și 6 vârfuri. Dacă aceeași construcție este executată cu 5 linii drepte, atunci primim un pentagon plin (85 - II). El, dacă presupunem că printre cele 5 linii drepte nu există perechi de paralel, 5 laturi și 10 vârfuri. Un șase partid plin (cu aceeași rezervare despre liniile drepte) 6 laturi și 15 vârfuri, etc.
78. Să luăm din nou câteva puncte și să le conectăm în perechi, dar nu fiecare cu fiecare, dar, după ce le-am determinat ordinea, fiecare cu una ulterioară (una din urmă cu prima). Cifra astfel construită se numește: un poligon simplu - pe negru. Sunt oferite 86 de imagini cu 5-gonzi și 6-gonzi simpli.
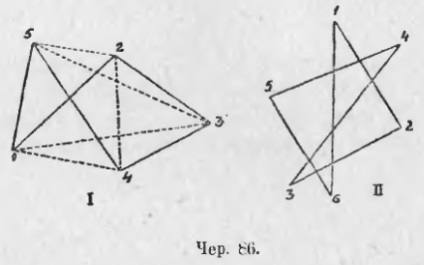
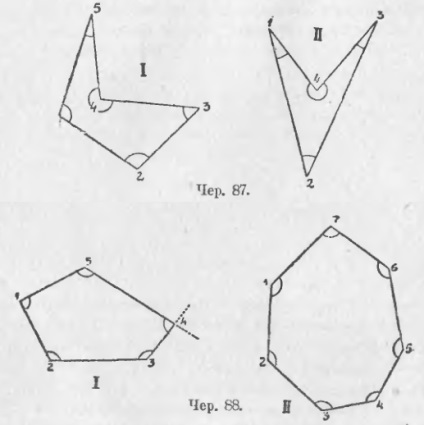
Ordinea punctelor din desen este indicată prin numere: aici este necesar ca cele trei puncte adiacente să nu se afle pe o singură linie. Fiecare punct, care face parte dintr-un poligon simplu se numește vârful său și fiecare linie - de partea lui (putem aici, așa cum a fost în triunghiul, pentru a înțelege sub acest nume doar un segment de linie care leagă două noduri adiacente ale poligonului). Nu este dificil să vedem că există atât de multe laturi într-un poligon simplu ca și vârfurile. Dacă conectat direct la două vârfuri neadiacente, atunci linia rezultată (sau segment, luat prizonier între vârfuri) este o diagonală a poligonului. Pe negru. 86 (I) este construit de linia punctată 5 a diagonalelor unui simplu pentagon. Într-un hexagon simplu este posibil să se construiască 9 diagonale (pe linia 86 - II nu sunt construite). Deoarece un poligon simplu are atâtea laturi ca și nodurile, ele pot fi denumite și multiplicatori simpli (pentagon simplu, etc.). Pe negru. 87 și 88 există în continuare diverse tipuri de poligoane simple.
79. În cursul geometriei elementare, sunt luate în considerare numai poligoane simple și, prin urmare, ele sunt adesea numite poligoane într-un singur cuvânt. În construcția poligoanelor simple pot fi două cazuri: 1) laturile poligonului, adică prin acel nume segmentele de linie între două noduri cruce reciproc (vezi iunie 86), și 2) nu se încrucișează (Iun 87 și 88) .... Între aceste două cazuri, există o diferență semnificativă. În timp ce în al doilea caz vom vedea că poligonul selectează din planul anumitor partea sa, care se numește zona poligonului, în primul caz, vom vedea că există mai multe părți - acest lucru este vizibil mai ales în iunie 86, II - și chiar uneori se pot distinge două astfel de părți, unul dintre ele fiind suprapus peste celălalt; aici, prin urmare, nu vedem imediat zona. delimitat de acest poligon. Prin urmare, vom numi poligoane potrivite pentru cel de-al doilea caz (cercurile 87 și 88) cu suprafață. și poligoane adecvate pentru primul caz (Figura 86) - care nu au o zonă (ele sunt de asemenea numite stellate).
Trebuie remarcat faptul că, făcând câteva condiții care permit părților planului să fie considerate pozitive sau negative, putem presupune că fiecare poligon are o zonă. Problema zonei poligoanelor stellate nu este inclusă în cursul geometriei elementare.
Adesea se consideră așa-numitul perimetru al unui poligon; Acest nume este suma tuturor laturilor poligonului.
80. În geometria elementară, poligoanele având o zonă sunt considerate aproape exclusiv. La fiecare vârf din colțurile poligonului sunt obținute la 4 la fiecare colț, în cazul în care una din laturile poligonului înțelese linii infinite (de ex. A se vedea. Unghiurile de la vârful pentagon I 4 Jun. 88). Unul dintre aceste colțuri, a cărui regiune interioară capturează zona poligonului, se numește interior; la fiecare vârf al poligonului obținut într-un colț interior (Iun. 87 și 88 colțuri interioare marcate arce).
Și aici există o separare de poligoane având o suprafață în două clase: 1) fiecare unghi intern al poligonului ca unghiul rectificat - sunt numite de poligon convex (88 iunie). 2) se poate întâmpla ca una sau mai multe unghiuri interne mai mari decât rectificat (la 87 unghiuri iunie la nodurile 4 din ambele poligoane.) - aceste poligoane sunt numite non-convexe.
Un poligon convex are proprietatea că toate vârfurile sale sunt situate pe o parte a fiecărei laturi (adică, prin acest nume, o linie infinită). Un poligon ne-convex nu posedă această proprietate.
În viitor, va trebui să ne ocupăm în principal de poligoane convexe.
81. Prima noastră sarcină cu privire la poligoane este de a găsi suma unghiurilor interioare ale unui poligon.
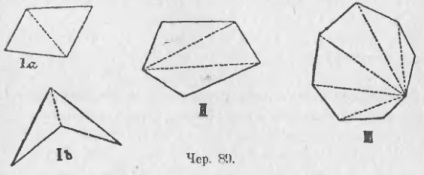
Dacă luăm un patrulater având o zonă [ 89, I (a) sau I (b)] și construi una dintre diagonalele sale - dacă (a) este indiferent care, în cazul I (b), cel care se află pe o suprafață de poligon cu patru laturi (în interiorul său ), atunci primim 2 triunghiuri. Suma unghiurilor interioare ale fiecărui triunghi 2d, prin urmare, suma unghiurilor interioare gon-4 = 2d * 2 = 4d. Dacă luăm o 5-gon și construi două diagonale de la unul dintre nodurile sale, obținem 3 triunghi (Iun 89, II.); ca suma unghiurilor interioare ale unui triunghi = 2d, atunci suma unghiurilor interioare ale 5-gon = 2d * 3 = 6d; De asemenea, pentru a obține 6-gon triunghi 4 și, prin urmare, suma unghiurilor sale interioare = 2d * 4 = 8d și t. d. Dacă luăm, de exemplu. 11-gon, după construirea diagonalelor obținem 9 triunghiuri. Suma unghiurilor interioare ale lui 11-gon = 2d * 9 = 18d. În general, dacă luăm n-gon, după construirea diagonalelor unuia dintre nodurile sale obține (n - 2) triunghiuri, și, prin urmare, suma unghiurilor interioare ale poligonului exprimat prin formula:
unde n reprezintă numărul de laturi sau vârfuri ale acestui poligon.
82. A doua întrebare va fi chestiunea sumei unghiurilor exterioare ale poligonului. Numit „coltul exterior“ poate fi înțeleasă, așa cum am făcut deja triunghiul, unghiul format o continuare a unei părți a poligonului cu următoarele părți (∠I, ∠II și așa mai departe. D. Iun. 90). Să mergem pe marginea acestui poligon, pe care îl vom considera convex, de exemplu. În direcția indicată de săgeți, fiecare parte continuă în aceeași direcție. Apoi obținem un număr de unghiuri externe: ∠I, ∠II etc. Să considerăm mai întâi o pereche de colțuri: .. interioare și exterioare, la un nod comun, de ex. ∠1 și ∠I; atunci vedem că suma lor este un unghi rectificat, adică,
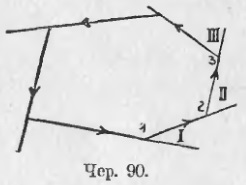
Constatat, de asemenea, la partea de sus a celeilalte: .. ∠2 + ∠II = 2d etc. Dacă presupunem că toate nodurile din poligon a fost n, cum ar fi perechile de unghiuri n, și, prin urmare:
(Suma unghiurilor interne) + (suma unghiurilor externe) = 2d * n
Dar știm asta
suma unghiurilor interne este 2d (n - 2).
Suma unghiurilor externe = 2dn - 2d (n - 2) = 2dn - 2dn + 4d = 4d
t. e. suma unghiurilor exterioare ale unui poligon convex nu depinde de numărul de laturi (sau noduri), iar acest poligon este întotdeauna 4d.
83. Anexă. De asemenea, puteți înțelege numele "colțul exterior" într-un alt sens. Să presupunem că avem un poligon (negru 91) având o zonă, deși nu convexă. Apoi, sub unghiul colț exterior poate fi înțeles laturile compuse ale poligonului și nu extensiile lor, precum și un unghi intern, de ex. ∠ BAC, dar pentru zona interioară a acestuia, luați acea parte a planului selectat de laturile acestui unghi, care nu include zonele acestui poligon. Interiorul fiecăruia dintre aceste colțuri este marcat în desen cu un arc. Apoi, fiecare astfel de unghi, împreună cu unghiul său intern corespunzător, este de 2 unghiuri rectificate sau 4d, de exemplu. intern ∠BAC + extern ∠BAC = 4d.
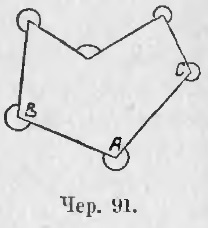
În cazul în care părțile au n poligon, suma tuturor interne și suma tuturor extern = 4d * n, și astfel cantitatea de unghiuri exterioare = 4dn - 2d (n - 2) = 4dn - 2dn + 4d = 2dn + 4d = 2d (n + 2).
- Construiți un hexagon complet. Câte părți are el?
- Construiți un șase fețe întregi, astfel încât să nu aibă laturi paralele. Câte vârfuri are?
- Găsiți o formulă generală pentru numărul laturilor unui n-gon complet și pentru numărul de noduri ale unui suporter n complet (presupunând că acesta din urmă nu are laturi paralele).
- Câte diagonale pot fi construite de la un vârf al unui simplu n-gon?
- Câte diagonale are un simplu n-gon?
- Exprimați în părțile unghiului drept fiecare colț interior al pentagonului convex, dacă acesta are toate unghiurile egale unul cu celălalt.
- Exprimați pentru pentagonul sarcinii anterioare fiecare colț exterior în părțile unghiului drept.
- Într-un triunghi isoscel, fiecare unghi la baza = ¾d. Găsiți (în părți ale unghiului drept) unghiul său la vârf.
- Într-un triunghi isoscel, unghiul de vârf este de 5/8 d. Găsiți unghiul în partea de jos.
- Într-un patrulater convex, unghiurile opuse sunt pereche egale una cu cealaltă. Pentru a afla că un astfel de patrulater este o paralelogramă.