Linia celei mai mari versanți este o linie dreaptă perpendiculară pe orice plan orizontal. L.N.S. este utilizată pentru a determina unghiul de înclinare a planului față de planul proeminențelor π1 - α (fig.55, 59). Linia AB este cea mai mare pantă. A'B'┴hoαα este unghiul de înclinare al lui AB la π1. Acesta este unghiul dintre proiecția orizontală și valoarea naturală a segmentului AB.
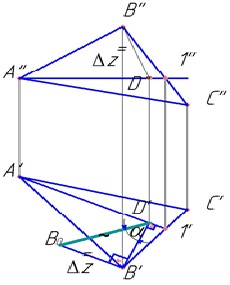
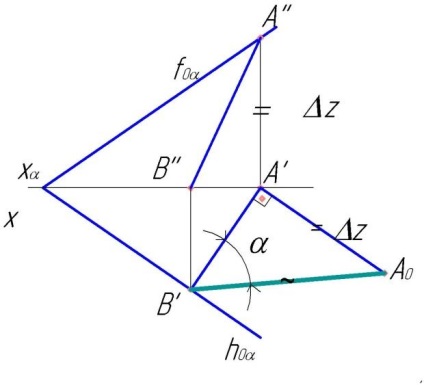
Determinați valoarea reală a segmentului AB. În proiecția orizontală, construim un triunghi drept cu picioarele A'B 'și Δz. Unghiul a între valoarea adevărată și proiecția orizontală a segmentului AB este unghiul de înclinare al planului față de planul orizontal al proeminențelor.
Figura 58 prezintă construcția LNS. BD.
Δ ABC a avut loc pe orizontală A1 și din orice punct al planului (în exemplul (∙) a avut loc în L.N.S. BD ( „┴A'1“ B'D) Unghiul α -. Este triunghiul ABC unghi față de planul orizontal al proiecției .
Construcția liniei de intersecție a două planuri
Două avioane se intersectează întotdeauna într-o linie dreaptă. Pentru a construi linia de intersecție, este suficient să găsiți două puncte ale acestei linii sau un punct și direcția acestei linii. Să luăm în considerare mai multe cazuri de intersecție a avioanelor.
Exemplul 1. Două planuri α și γ se intersectează pe o linie dreaptă MN (Figura 60) în limitele desenului.
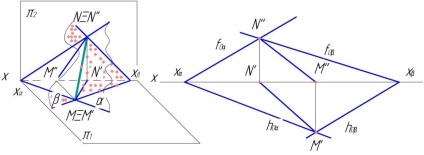
Exemplul 2. Intersecția a două planuri are loc orizontal (sau frontal).
În figurile 61, 62 proiecția frontală a liniei de intersecție coincide cu traiectoria lui f0γ. iar orizontul este ușor de găsit ca o proiecție orizontală a orizontalei în acest plan.
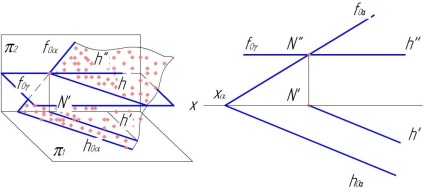
Exemplul 3. În cadrul desenului se intersectează numai două piste orizontale ale planurilor a și β date date (figura 63).
Gasim punctul M la intersectia urmelor orizontale. Pentru a găsi punctul N, luăm un plan orizontal suplimentar auxiliar γ. Acest plan secant va intersecta planurile α și β de-a lungul orizontalelor. Proiecțiile orizontale ale acestor contururi la intersecția vor da cel de-al doilea punct al liniei de intersecție a planurilor α și β - punctul N (Fig.64).
Exemplul 4. Un plan este dat de urme de poziție generală, al doilea plan este dat de două linii intersectate de poziție generală (Fig.65).
1. Desenați un plan auxiliar al poziției particulare, de exemplu planul nivelului orizontal β || π1 (fωβ || x) (figura 66).
2. Planul β intersectează planul α orizontal h.h "

3. Planul β intersectează planul (a∩b) de-a lungul liniei drepte (2-3).
4. Liniile h și 2-3 se intersectează în punctul M (M 'și M "). unde M '= h'∩ (2'-3') și M "

5. Pentru a construi cel de-al doilea punct comun, tragem un alt plan auxiliar γ || π1 (fογ || x) (figura 67).
6. Planul γ intersectează planul α orizontal h1: h1 "

7. Planul γ intersectează planul (a∈b) de-a lungul unei linii drepte (5-6).
8. Liniile h1 și 5-6 se intersectează la punctul M (M "și M"). unde M '= (5'-6') ∩h1 ', M' '

9. Conectați aceleași puncte numele de proiecție M și N și de a primi linia de intersecție a proiecției (M'N „) și (M''N“ „).
Exemplul 5. Planul ΔABC al unei anumite poziții (ΔABC
De la AABC
1. Observați proiecțiile orizontale generale ale Q 'și T' la intersecția proeminențelor orizontale ale triunghiurilor ABC și MNK (figura 69).
2. Căutăm proiecțiile frontale Q '' și T '' pe liniile conexiunii de proiecție din ΔM''N''K ''.
3. Linia de intersecție QT este definită de QT (Q''T '' și Q'T ').
4. Determinați vizibilitatea figurilor plane, t. planurile sunt considerate opace. Vizibilitatea proiecției orizontale a figurilor nu trebuie determinată, deoarece ΔAVS proiectat într-o proiecție linie dreaptă M'N'K „vizibile. Definim vizibilitatea figurilor plane în raport cu planul proiecțiilor π2. Pentru aceasta considerăm punctele concurente 1 și 2 se intinda pe liniile oblice Soare și MK. 1 proiecție frontală „și 2„sunt la fel, și o proiecție orizontală 2' este situat în fața proiecția orizontală 1“. Punctul 1 "este invizibil față de planul proiecțiilor π2. Mai departe, argumentăm după cum urmează: punctul 2 se află pe AABC. în consecință, ΔA''V proiecție frontală ''S «vizibil pe π2 pe partea în care punctele 1» și 2 «». După linia de proiecție frontală de intersecție Q „și T“ vizibilitate ΔA''V ''S «» este inversată, adică, devine invizibil (figura 69).