85. Construim un isoscel AABC (mod 92) cu AB = BC. Atunci știm că unghiurile sale la bază sunt egale, adică, ∠A = ∠C. Numărăm aceste unghiuri, apoi ∠1 = ∠2. Să construim acum noile triunghiuri ABC, ABC, etc., astfel încât laturile AB și ∠B să rămână neschimbate, dar partea BC crește. Apoi, unghiul A ar trebui să crească (ceea ce este evident), iar unghiul C va scădea: vedem că ∠3 <∠2, ∠4 <∠3 и т. д. потому что ∠2 есть внешний угол для ∆ACC' и, следов. ∠2> ∠3 sau ∠3 <∠2, также ∠3 есть внешний угол ∆AC'C'' и, след. ∠3> ∠4 sau ∠4 <∠3 и т. д. (уменьшение угла C видно еще из того, что сумма углов треугольника всегда равна 2d: угол B не изменяется, угол A увеличивается, – след. ∠C должен уменьшаться).
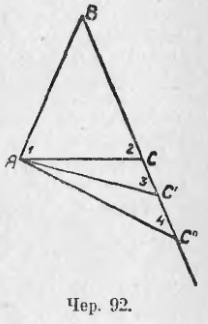
Din aceste construcții avem dreptul să tragem concluzii:
1) Dacă două laturi sunt egale într-un triunghi, atunci unghiuri egale sunt plasate împotriva lor.
2) Dacă cele două laturi nu sunt egale în triunghi, atunci unghiul mai mare se află în raport cu cel mai mare.
86. Acum, dimpotrivă, construim: 1) un triunghi cu două unghiuri egale și 2) un triunghi cu două unghiuri inegale și comparăm laturile opuse acestor unghiuri. Pentru a rezolva problemele care apar aici, vom folosi metoda de raționament, adesea folosită în matematică.
1) Fie ΔABC (93) constant, astfel încât ∠A = ∠C. Comparați laturile BC și BA.
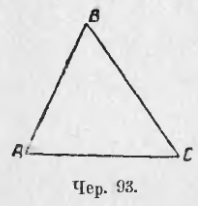
Până acum, fără a cunoaște nimic despre părțile AB și BC, putem face 3 ipoteze despre ele: 1) AB = BC, 2) AB> BC și 3) AB
Dacă două unghiuri sunt egale în triunghi, atunci părțile egale se află împotriva lor.
2) Fie ΔABC (93) constant, astfel încât ∠A> ∠C. Comparați laturile BA și BC. Dacă două colțuri în triunghi sunt inegale, atunci partea mai mare se află în fața celei mai mari. Acum, întrebările sunt rezolvate cu ușurință: 1) care dintre laturile unui triunghi dreptunghiular este cea mai mare? 2) Care parte a triunghiului obtuz este cea mai mare? 87. În cele două paragrafe precedente. ne-am ocupat cu două poziții: 1) față de latura mai mare este mai mare unghi și 2) în raport cu unghiul mai mare este o mare petrecere. Am descoperit că aceste gânduri sunt adevărate pentru un triunghi. Se pune întrebarea dacă acestea sunt valabile pentru două triunghiuri. Fără îndoială, este adevărat pentru două triunghiuri egale. deoarece triunghiurile egale pot fi îmbinate într-un singur triunghi prin suprapunere. Dar, în general vorbind, două triunghiuri diferite (nu sunt egale), nu pot fi aplicate aceste prevederi: putem construi două astfel de triunghiuri ΔABC și ΔA'B'C „(. 94 iunie) Asta a fost ∠B> ∠B“ , dar AC ar fi Acest caz este ușor de înțeles vizual. Luăm două tije AB și BC (95bis) și le adăugăm până la capăt (la punctul B). Dacă rotiți bagheta BC în apropierea punctului de săgeată B, au ∠B va crește: BC laterală se va schimba poziția lor (chiar dacă unul dintre ei are un BC „), dar tot timpul BC rămâne egală cu ea însăși; segmentul AB de asemenea nu se schimba. Rețineți că punctele A și C definesc un alt segment AC, care nu este prezentat în desen. Când deasupra punctului de rotație C își schimbă poziția și este clar că acest segment de curent alternativ, care nu este prezentat în desen, trebuie crescută (de ex. AC „> AC), m. E. Dacă cele două laturi ale triunghiului nu sunt schimbate, iar unghiul micșorează crește, atunci și partea terță crește. În text, acest caz este clarificat fără ajutorul unei astfel de reprezentări vizuale.
Din nou, putem face 3 ipoteze: 1) AB = BC, 2) AB> BC și 3) AB 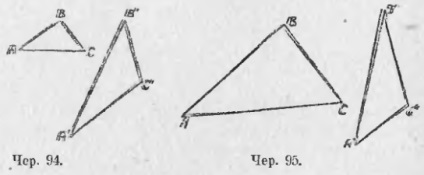
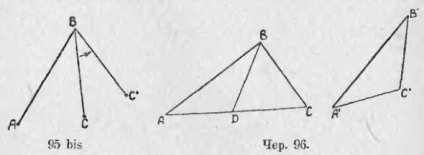
Construim două astfel de triunghiuri, astfel încât să aibă două laturi egale, dar unghiurile dintre ele nu sunt egale. Să presupunem că în ΔABC și în ΔA'B'C '(bar 95) avem AB = A'B', BC = B'C ', dar ∠B> ∠B'. Să comparăm laturile AC și A'C, care se află sub unghiuri inegale. În acest scop, aplicăm ΔA'B'C 'la ΔABC astfel încât partea A'B' să coincidă cu partea AB. Atunci partea B'C 'trebuie să intre în interiorul ∠B, deoarece ∠B' <∠B, но где кончится эта сторона, т. е. где расположится точка C', неизвестно. Может быть, она расположится как раз на стороне AC, может быть, расположится вне ∆ABC, а может быть внутри этого треугольника. Разберем эти три случая отдельно.
1) Fie ΔA'B'C 'poziționat astfel încât să ia poziția ΔABD (figura 96), astfel încât punctul C' să cadă în D, pe partea AC; apoi, evident, AD 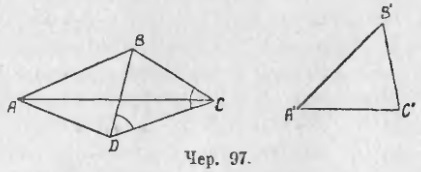
2) Să ΔA'B'C 'poziție la aplicare ia ΔABD (Iun. 97), m. F. Punctul C' situat în punctul D, este ΔABC. Apoi, conectați punctele C și D, Primirea ΔBCD, care BC = BD, deoarece, prin construcție, B'C „= BC și BD au aceeași B'C lateral“, doar transferat într-o altă locație. Prin urmare, ΔBCD este isoscele și ∠BCD = ∠BDC. Luați în considerare acum ΔACD; aproximativ două din colțul său, și este vorba de ∠C (sau ∠ACD) și aproximativ ∠D (sau ∠ADC), este ușor să dau seama, folosind unghiuri egale marcate ale unui triunghi isoscel, care unul este mai mare decât altul. De fapt, vedem că ∠ACD <отмеченного угла BCD при основании равнобедренного треугольника, а ∠ADC> marcajul unghiului BDC la baza unui triunghi isoscel. Dar ∠BCD = ∠BDC, prin urmare, ∠ADC> ∠ACD. Prin urmare, pe baza punctului 86 (aplicându-l la ΔACD) avem AC> AD, dar AD este partea A'C 'transferată în alt loc, deci AC> A'C'.
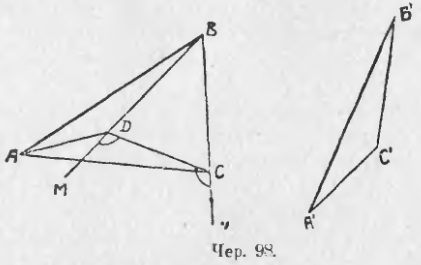
3) Să ΔA'B'C 'poziție la aplicare ia ΔABD (Iun. 98), t. E. Punctul C' dispus în ΔABC. Apoi, conectarea punctelor C și D, obținem isoscel ΔCBD (BD = BC, BD este B'C lateral 'transferat într-o altă poziție, iar B'C' = BC de construcție) și, în consecință, ∠BCD = ∠BDC . Dacă vom continua partea BD și BC în direcțiile DM și CN, obținem două unghi exterior al unui triunghi isoscel și ∠MDC ∠NCD, dar ∠MDC = ∠NCD, prin urmare, ∠ADC> ∠ACD și, prin urmare, în baza p. 86, avem AC> AD, sau AC> A'C '(AD au parte A'C', redirecționat către o altă poziție).
Deci, în toate cele trei cazuri sa dovedit asta
adică dacă două laturi ale unui triunghi sunt egale cu două laturi ale unui alt triunghi, dar unghiurile dintre ele nu sunt egale, atunci partea mare se află pe un unghi mare.
88. Să analizăm întrebarea inversă. Să presupunem că ΔABC și ΔA'B'C '(95) sunt construite astfel încât AB = A'B', BC = B'C ', dar AC> A'C', adică două triunghiuri au două părți egale, dar părțile terțe nu sunt egale. Comparați ∠B și ∠B '.
Folosim aceeași metodă de raționament ca în §86.
Atâta timp cât putem face trei ipoteze despre unghiurile B și B ': 1) ∠B = ∠B', 2) ∠B> ∠B 'și 3) ∠B <∠B'.
Prima ipoteză nu este validă, de vreme ce triunghiurile noastre, având două laturi egale și unghiuri egale între ele în construcții, ar fi egale și, prin urmare, AC '= A'C', iar acest lucru contrazice construcția. A treia ipoteză este că ∠B <∠B' также не годится, так как тогда к этим треугольникам был бы применим результат, найденный в предыдущем п. на основании которого имели бы AC
Dacă cele două laturi ale unui triunghi sunt egale cu cele două laturi ale celeilalte, respectiv, dar părțile terțe ale acestor triunghiuri nu sunt egale, atunci unghiul mai mare se află și față de partea mai mare.