
Lecția de prezentare însoțită care cuprinde diferite tipuri de probleme la utilizarea graficelor: problemă rezolvată cu utilizarea finală aritmetică a reziduurilor problemă pe probleme de interes în care predeterminate grafic planar necesară pentru a parcelei fără a ridica creionul pe hârtie și nu încercuiește de două ori aceeași parcelă grafic . Teoretic, materialul pentru lecție conține conceptul contelui, o margine, chiar, ciudat grafic Lecția cuprinde etapele de: un cont verbal, verificați Utilizare acas joc de lucru contra, teme pentru acasă, rezumat lecție. Prezentarea conține materiale istorice despre Euler și declarații frumoase.
Rezolvați problemele utilizând graficele din clasa a 5-a.
să consolideze noțiunea de grafic și să dezvolte abilitățile de a folosi grafice pentru rezolvarea problemelor;
verificați nivelul de mastering a conceptului graficului prin capacitatea de a aplica cunoștințele disponibile pentru a rezolva noi probleme.
să dezvolte gândirea logică și creativă a studenților, ingeniozitatea, observația, intuiția și adecvarea în evaluarea muncii unui coleg de clasă;
formează un interes cognitiv activ în subiect.
Pentru a educa respectul pentru personalitățile istorice, dragostea literaturii pe exemplul textelor sarcinilor selectate.
1. Moment organizatoric
2. Verificarea temelor
"Viața este împodobită cu două întrebări: ocupația matematică și predarea ei" Poisson S.II.
Studiul matematicii se desfășoară în procesul de rezolvare a problemelor și exercițiilor.
Băieți, astăzi la lecție vom rezolva problemele legate de grafice, rezolvate de la sfârșit, folosind aritmetica reziduurilor, sarcini pentru procente.
Să începem cu sarcina de origine pentru interes
5 ∙ 0,35 = 1,75 litri de grăsime în 5 litri de cremă
4 ∙ 0,20 = 0,8 litri de grăsime în 4 litri
1,75 + 0,8 = 2,55 litri de grăsime în amestec
5 + 4 + 1 = amestec de 10 litri
5. 2,55: 10 = 0,255 litri = 25,5% conținut de grăsime din amestec
Vom juca jocul: "Cel mai bun contra" (pentru evaluare).
Selectați 2 contoare din fiecare rând.
Pestalozzi a mai spus: "Contul și calculele sunt baza ordinii în cap"
Să aflăm - care dintre voi va răspunde corect la mai multe întrebări. Băieți, ajutați - numărați răspunsurile corecte ale copiilor dvs.
1) Fizicianul, obosit, sa dus la culcare la ora 22; pre-alarmă pentru 12 ore a doua zi. Câte ore a dormit înainte de ceasul de alarma îl ridică? [2]
4) Care va fi restul de împărțire a produsului cu 6
67 = 1 (Mod 6) (Aceasta este sarcina pentru aritmetica reziduală)
5) Găsiți restul diviziei cu 5 următoarea sumă (7 + 56 + 558 + 5558) / 5
6) Rezolvare yp - e: (((x + 2) / 4) -2) * 6 = 12 [14]
7) Găsiți numărul dacă 3% din acesta este 24 [800]
9) 3000% din 50 [1500]
10) Găsiți procentul de numere de la 48 la 16 [300%]
11) Calculați 0,1% din valoarea de 700 [0,7]
Toată lumea a câștigat-o, deoarece toată lumea a participat cu ei și a verificat corectitudinea răspunsurilor.
4) Matematicianul remarcabil Kovalevskaya a subliniat: "Matematicienii
există o limbă - acestea sunt formulele "
Probleme rezolvate de la sfârșit
(Scena) "Țăranul și diavolul":
Țăranul merge și plânge: "Ema! Viața mea este amară! Zaela are nevoie absolut! Aici, în buzunar, doar câțiva bani de cupru se încurcă, iar acum trebuie să li se dea. Și cum se întâmplă cu ceilalți că primesc bani pentru toți banii? Bine, cel puțin cineva mă va ajuta.
Numai a avut timp să spună acest lucru, cum să se uite, iar în fața lui se află diavolul.
-Ei bine, - spune el, - dacă vrei, te voi ajuta. Și acest lucru nu este deloc dificil. Vedeți podul peste râu?
-Văd! Spune țăranul și el însuși sa speriat.
-Ei bine, deci merită să vă traversați numai podul - veți avea de două ori mai mulți bani decât există. Te vei întoarce, din nou va fi de două ori mai mare decât a fost. Și de fiecare dată când treci podul, vei avea de două ori mai mulți bani ca înainte.
-Oh, da? Spune țăranul.
-Cuvântul potrivit! - asigură diavolul. - Numai, chur, persuasiune! Pentru că îmi dublez banii, de fiecare dată când treci podul, dă-mi 24 de copeici. În caz contrar, nu sunt de acord.
-Păi, nu contează! Spune țăranul. - Odată ce banii vor fi dubluți, de ce să nu vă dați 24 de copeuri de fiecare dată? Să încercăm!
A traversat podul odată, a numărat banii. Într-adevăr, a devenit de două ori mai mare. El a dat 24 de copeici diavolului și a trecut a doua oară. Din nou, au fost de două ori mai mulți bani ca înainte. A numărat 24 de copeici, a dat linia și a trecut a treia oară podul. Banii au fost din nou de două ori mai mult. Dar numai sa dovedit că au fost doar 24 de copeici, care, prin acord, au trebuit să dea linia. Le-a dat departe și a rămas fără un ban.
Cât a mai avut țăranul mai întâi banii?
1. ((2 - 24) 2 - 24) 2 - 24 = 0 x = 21
Dacă după ultima trecere țărănistul a dat 24 de ani, apoi înainte de 12 ani, adăugăm 24 (pe care le-a dat) obținem 36 de mijloace, înainte de a doua trecere a fost de 38 de copeici. Pentru ei a adăugat 24, avem 42, înseamnă că au fost 21 de polițiști.
A pierdut țăranul. Se poate vedea că sfatul altcuiva trebuie întotdeauna să-și facă propriul.
5. Sarcini pentru grafice.
Teoria grafurilor găsește aplicabilitate, nu numai în matematică, ci, de exemplu, în sistemele geoinformation (GIS). .. existente sau case, clădiri, cartiere, etc., sunt considerate ca partea de sus nou proiectat, și conectarea acestora drumuri, rețele de utilități, linii electrice, etc. - .. Ca coaste. Aplicarea diferitelor calcule efectuate pe un astfel de grafic, care permite, de exemplu, pentru a găsi cel mai scurt ocol sau cel mai apropiat magazin alimentar, planul de cel mai bun traseu.
Primul tip de sarcini
"Cine joacă Lyapkin-Tyapkin?"
În cercul de teatru școlar a decis să pună "Inspectorul" lui Gogol. Apoi a izbucnit un argument aprins. Totul a început cu Lyapkin-Tyapkin. "Lyapkin-Tyapkin va fi eu!" a spus Gene decisiv.
- Nu, o să fiu Lyapkin-Tyapkin, exclamă Dima.
- De la copilărie am visat să întruchipez această imagine pe scenă.
- Ei bine, sunt de acord să renunț la rol, dacă m-au lăsat să joc Khlestakov, - a arătat generozitatea lui Gen.
-. Și eu - Osip, - nu i-am oferit în generozitatea lui Dima. "Vreau să fiu o căpșună sau un guvernator", a spus Vova.
- Nu, voi fi guvernatorul, strigă Alik și Borya în mod unison. "Sau Khlestakov," adăugau în același timp.
Rolele vor fi distribuite astfel încât artiștii să fie fericiți? (Nu ne întrebăm dacă audiența va fi mulțumită.)
Din fiecare participant tragem segmentele, adică Marginile la rolurile pe care dorește să le joace. Avem un grafic cu zece noduri și zece margini. Este necesar ca zece să aleagă cinci margini care nu au noduri comune.
Gena Dima Vova Boria Alik
Lyachpin-Khlestakov Osip Strawberry
Faceți-o ușor. Este suficient să rețineți că un vertex duce la vârfurile 3 și 4, respectiv de la vârfurile DiB. Aceasta înseamnă că Osip (top 3) ar trebui să joace Dima (cine altcineva) și Strawberry Vova. Vertex 1 Lyapkin- Tyapkin-conectate prin margini la D și E. Rib 1- D este inutilă, pentru că Dima este deja ocupat, este fin 1 G, Lyapkina- Tyapkina pentru a juca Gene. Rămâne să conectăm vârfurile A și B cu nodurile 2 și 5, corespunzătoare rolurilor lui Khlestakov și Gorodnichy. Acest lucru se poate face în două moduri: fie selectați coaste A - 5 și B-2 sau marginile A-2 și B-5. În primul caz, Alik va juca guvernatorul, iar Boria-Khlestakov, în al doilea caz, dimpotrivă. După cum arată graficul nostru, nu există alte soluții la problemă.
Al doilea tip de sarcini. în care trebuie să se tragă un graf plat, fără să se ia creionul din hârtie și să nu se circulă de două ori aceeași secțiune a graficului. Dacă în acest caz o linie închisă începe și se termină la același vârf, atunci un astfel de grafic este numit Euler
Dacă toate nodurile grafice sunt egale, atunci graficul poate fi bypassed într-un singur ciclu, fără a trece de două ori o margine.
Dacă 2 vârfuri de ciudat, bucla închisă nu există, dar poate fi provine de la unul vârfuri impare în jurul întregului grafic și a reveni la partea de sus a doua ciudat.
1. O anecdotă este bine cunoscută: Cineva a dat 1000000 de ruble tuturor celor care vor trage următoarea figură.
Cerință: printr-un accident vascular cerebral continuu, adică fără îndepărtarea pixului sau a creionului de pe hârtie și dublarea niciunei linii.
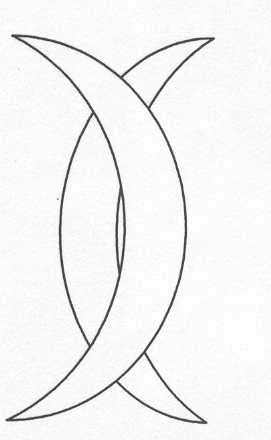
2
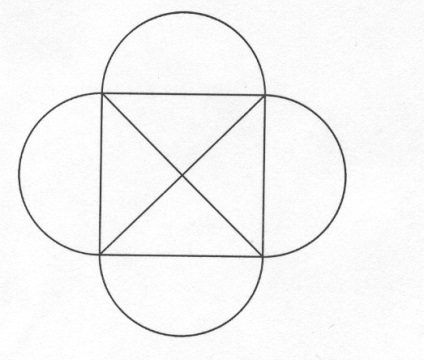
. Mohamed, în loc de semnătura (el era analfabet), descris într-o singură lovitură constând din
3
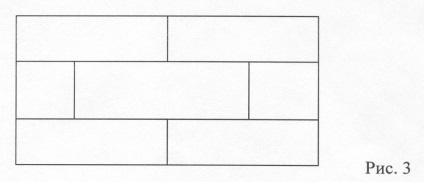
. Nu puteți trage un accident vascular cerebral într-o singură lovitură în figura prezentată în figura 3. Explicați de ce
4. Acoperișul a urcat în borcan din sub zahăr. Banca are forma unui cub. Dacă zbura poate ocoli în mod constant toate cele 12 margini ale unui cub, fără a trece de două ori pe o margine, nu este permis să sară și să zboare de la un loc la altul în loc.
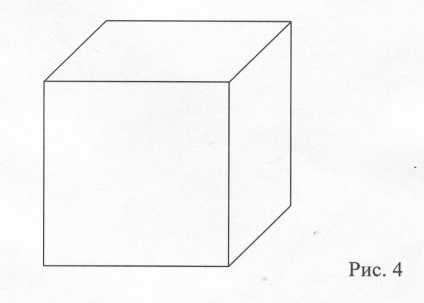
Niven a remarcat: "Matematica nu poate fi studiată observând modul în care o face vecinul"
6. Temă: Pot fi pictate figurile din desene vopsite într-o singură lovitură? (rezolvată cu ajutorul graficului)
Astăzi ne-am întâlnit cu o altă metodă de rezolvare a problemelor cu ajutorul graficelor.
Partea instructivă a acestor sarcini este de a investiga dacă este posibilă sau nu o soluție la această problemă înainte de a decide cu privire la soluția în sine.
Încă o dată am văzut că grafic teorie poate rezolva sarcinile rapid și elegant, care sunt foarte dificil de a rezolva alte metode și face posibilă nu numai pentru a rezolva o problema luate separat, dar, de asemenea, să găsească metode pentru a rezolva o clasă de probleme.
În concluzie, vreau să spun următoarele: "În sarcinile pe care viata le pune în fața noastră, examinatorul este însăși natura.