2 Capitolul 1. descompunerea unui vector în raport cu doi vectori noncoliniari. Lemma pe vectori coliniari. O lemă pe vectori coliniari. Dacă vectorii a și coliniar și a = 0, atunci există un număr R, = Ra.Esli că vectorii a și coliniar și a = 0, atunci există un număr R, care Ra =. Dovada: Dovada: pentru probă, sunt posibile două cazuri. pentru probă, două cazuri sunt posibile. 1 și c. Luăm numărul R = | | a |. Deoarece R0, vectorii Ra și B sunt co-direcționați (Figura 1). În plus, lungimile lor sunt egale cu: | Rα | = | R | | | а | = | | a | · | a | = | in. De aceea, in = Rα. 2 și în. Luăm numărul R = - | | a |. Deoarece R0, vectorii Ra și B sunt din nou co-direcțional (figura 2). Lungimile lor sunt, de asemenea, egale: | Rα | = | R | | | а | = | | | | | | a | = | în. | Prin urmare, = = Ra. Lemma este dovedită. Figura 1 Figura 2 a a a a R a R |

Teoremă: Orice vector poate fi descompus în două vectori non-coliniari, iar coeficienții expansiunii sunt determinați în mod unic. Dovada: Fie a și b date vectoriale non collineare. Mai întâi demonstrăm că orice vector p poate fi extins în termenii vectorilor a și b. Există două cazuri posibile. Dar vom lua în considerare primul caz. Vectorul p este colinar cu unul dintre vectorii a și b, de exemplu vectorul b. În acest caz, prin vectori coliniare Lema de vector p poate fi reprezentat ca p = y · b, în cazul în care există un număr y, și, prin urmare, p = 0 · a + y · b, adică. vectorul p este descompus de-a lungul vectorilor a și b. a b c

4 Conceptul de sistem de coordonate dreptunghiulare este cunoscut de la cursul de algebră. Reamintim că, pentru a defini un sistem de coordonate rectangular nevoie să dețină două linii perpendiculare reciproc pe fiecare dintre ei să aleagă direcția (care este indicată printr-o săgeată) și selectați unitatea de segmente de măsurare. Când se selectează unitatea de măsură a segmentelor, lungimea fiecărui segment este exprimată printr-un număr pozitiv. În cele ce urmează, pe lungimea unui segment vom înțelege acest număr. Amînarea originea O vectorilor de unitate (adică. Vectorul de lungime egală cu o) i și j, astfel încât vectorul direcție i coincide cu direcția axei Ox, iar direcția vectorului c j- direcția axei Oy (Fig.1). Vectorii i și j sunt numiți coordonatele vectorului. Vectorii de coordonate nu sunt coliniari, deci orice vector p poate fi extins în vectori de coordonate, adică pot fi reprezentate în forma p = xi + yj, unde coeficienții de expansiune (numerele x și y) sunt determinate în mod unic. Coeficienții expansiunii vectorului p prin vectori de coordonate se numesc coordonatele vectorului p în sistemul de coordonate dat. Scrieți coordonatele vectorului în paranteze curbate după desemnarea vectorului: p. În figură (figura 1) OA, b. Deci, modul în care vectorul zero poate fi reprezentat în forma 0 = 0 · i + 0 · j, atunci coordonatele sale sunt zero: 0. Dacă vectorii a = x 1 i + y j 1 și b = x 2 i + y j 2 sunt egale, atunci x 1 = x 2 și y 1 = y 2 coordonate, astfel, respectiv vectori egali. x y j i A O B C -2j 3i3i b

5 Mai important, trebuie să vă amintiți regulile care vă permit să găsiți coordonatele sumelor, diferența și produsul vectorilor printr-un număr din coordonatele vectoriale. 1! Fiecare coordonată a sumei a doi sau mai mulți vectori este egală cu suma coordonatelor corespunzătoare ale acestor vectori (A + b sunt egale). 2! Fiecare coordonată a diferenței dintre doi vectori este egală cu diferența dintre coordonatele corespunzătoare ale acestor vectori (A-b sunt egale). 3! Fiecare coordonate a produsului unui vector cu un număr este egală cu produsul coordonatelor vectoriale corespunzătoare prin acest număr. (Ie)

6 Sarcina 1. 3a-xb = ya + b; y = 3, x = -1. Sarcina 2. 4a-xa + 5b + yb = 0; 4a + 5b = xa-yb; x = 4, y = -5.
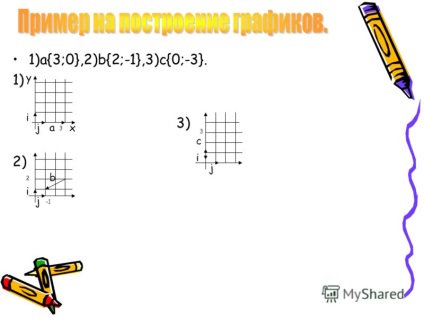
7 1) a, 2) b, 3) c. 1) 2) i jax y b j i 3) c 3 i j 2 3