LECȚIA: "DECOMPONZIUNEA VECTORULUI ÎN DOUĂ VECTOARE NEC COLLINARE"
Subiect: Descompunerea unui vector în raport cu doi vectori noncoliniari
Clasa: Gradul 9
Profesor:. director adjunct pentru activități educaționale. profesor de matematică și informatică.
Instituție de învățământ: școala generală Shura din regiunea Kemerovo
Orașul actual: Кемеровская область
Cunoașteți formularea și dovada lemnei pe vectori coliniari și teorema expansiunii pentru doi vectori noncoliniari;
Pentru a putea rezolva problemele prin aplicarea cunoștințelor dobândite.
I. Moment organizatoric: denumiți obiectivele lecției.
III Explicarea materialului nou:
1. Extinderea unui vector în raport cu doi vectori noncoliniari.
La rezolvarea problemelor, devine adesea necesar să se exprime un vector prin vectori deja dați. O astfel de operație se numește expansiunea unui vector în raport cu vectorii noncoliniari.
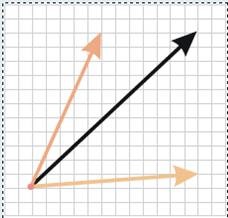
2. Lemma pe vectori coliniari.
O lemă este o declarație auxiliară, prin care se demonstrează următoarea teoremă sau mai multe teoreme.
Teorema: dacă vectorii sunt atât coliniari cât și # 61625; 0, atunci există un număr k astfel încât = k.
Întrucât vectorii luați în considerare sunt colinativi prin ipoteze, aceștia pot avea aceleași direcții. Să luăm în considerare două cazuri în care vectorii sunt simultan direcționați și direcționați opus.
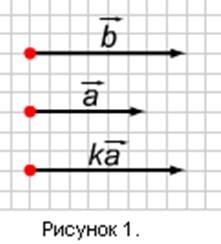
1). Să luăm un număr. Deoarece k ³, vectorii k și co-directional (Figura 1). În plus, lungimile lor sunt egale cu: k1 k1 = k1 1 k1 = k1 1 = k1 1. Prin urmare = k
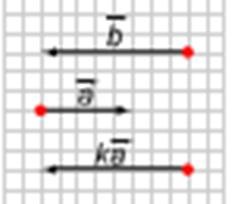
3. O teoremă privind descompunerea unui vector în raport cu doi vectori noncoliniari.
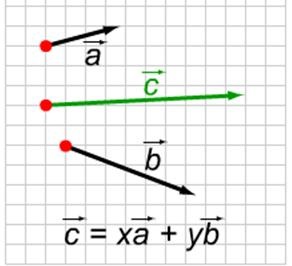
Fie vectorilor non collineari vectori, vectorul este reprezentat în formă
= x + y, unde x și y sunt anumite numere. Este obișnuit să spunem că vectorul este descompus în vectori și. Numerele x și y sunt numite coeficienții de expansiune.
Există două cazuri posibile:
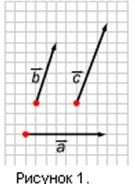
2) Vectorul nu este coliniar fie vectorului, fie vectorului. Observăm un punct O și amânăm vectorii =, =, = (Figura 2).
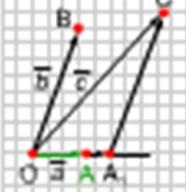
Acum demonstrăm că coeficienții x și y ai expansiunii sunt determinați în mod unic. Presupunem că împreună cu descompunerea = x + y, avem o altă descompunere = x1 + y1. Dacă deducem a doua egalitate de la prima și folosind regulile de acțiune asupra vectorilor, obținem = (x-x1) + (y-y1). Această egalitate poate fi satisfăcută numai dacă coeficienții x-x1 și y-y1 sunt zero. De fapt, dacă presupunem, de exemplu, că x-x1 0 0, atunci din egalitatea rezultată găsim = - și, prin urmare, vectorii sunt coliniari. Dar aceasta contrazice ipoteza teoremei. În consecință, x-x1 = 0 și y-y1 = 0, de unde x = x1 și y = y1. Aceasta înseamnă că coeficienții vectorului sunt determinați în mod unic. Teorema este dovedită.
1. O lemă este o declarație auxiliară utilizată în dovada uneia sau mai multor teoreme.
2. Lemma (pe vectori coliniari). Dacă vectorii sunt ambele coliniari și vectorul # 0, atunci există un număr k astfel încât = k
3. Fie vectori non-collinear, vectorul este reprezentat în formă
= x + y, unde x și y sunt anumite numere. Este obișnuit să spunem că vectorul este descompus în vectori și. Numerele x și y sunt numite coeficienții de expansiune.
4. Teorema: Orice vector poate fi descompus in doua vectori non-collineari, iar coeficientii expansiunii sunt determinati in mod unic.
IV. Consolidarea cunoștințelor dobândite:
1. Diagonalele paralelogramei ABCD se intersectează la punctul O. Exprimă vectorul prin vectori.
4. № 000 (a, d). Diagonalele paralelogramului se intersectează la punctul O, iar M este punctul central al segmentului AO. Găsiți, dacă este posibil, un număr k astfel încât egalitatea: = k, = k
5. Având în vedere un triunghi arbitrar ABC cu mediana AD. Găsiți modul în care vectorul este exprimat în termeni de vectori și.
V. Sumarizarea.
VI. Cesiune în casă: articolul 86, №№ 000 (in, г), 912 2,3 coloană), 916 (в, г)