Material didactic pentru munca unui tutore de matematică cu un elev de clasa a VIII-a de abilități slabe și medii. Cartea de bază privind geometria - celule Atanasyan 7-9. Aproape toate sarcinile sunt concepute astfel încât prima este rezolvată în colaborare cu tutorele, iar cea de-a doua rămâne pentru temă. Al doilea diferă de primul numai din cifre.
№1. În paralelogramul ABCD, înălțimea BH este de 4 cm, iar partea BC BC = 10 cm. Găsiți zona paralelogramului.
№2. În trapezoidul ABCD CH - înălțime, BC = 2cm, AH = 3cm, HD = 5cm, CH = 4cm. Găsiți zona acestui trapez.
№3. În paralelogramul MNKP, MT este bisectorul unghiului M. Se știe că NT = 5cm, TK = 3cm. Găsiți perimetrul unui paralelogram dat.
4.1 În trapezul MNKP, baza superioară a NK și linia mijlocie AB sunt de 5 și respectiv 9 cm.
Găsiți baza sa inferioară.
În trapezul PQNE, baza inferioară PE și linia mijlocie KN sunt de 10 și respectiv 7 cm. Găsiți baza sa superioară.
№5.1 În dreptunghiul ABCD sunt desenate bisectricele unghiurilor A și D care se intersectează la punctul M care se află pe partea B. Se găsește perimetrul ABCD. dacă AB = 6 cm.
№5.2 a avut loc în unghiul bisector ABCD dreptunghi A, care împarte BC lateral în lungimi de 5 cm și 3 cm. Gasiti perimetrul unui dreptunghi ABCD.
6.1 Punctele A, B, C, D sunt marcate pe cerc, astfel încât AB este diametrul său, iar unghiul ACD este egal cu. Găsiți unghiul DСВ.
№6.2 Cercurile A, B, C, D sunt marcate pe cerc, astfel încât diametrul AC, unghiul ACD este egal, iar unghiul BAC este egal. Găsiți unghiul BCD.
№7.1 Punctele B, N și D sunt marcate pe cerc. Unghiul BND este egal cu. Găsiți unghiul BDD.
Cercurile B, K și C sunt marcate pe cerc. Unghiul BOC este. Găsiți unghiul VCS.
8.1 În triunghiul dreptunghiular ACB, cuspul SV este de 4 cm, unghiul B este egal. Găsiți hypotenuse AB.
№8.2 În triunghiul dreptunghiular ACB, CA catenar este de 3 cm, unghiul A este egal cu. Găsiți hypotenuse AB.
Nr. 9 * În trapezoidul ABCD AB = CD, AC = 5cm, CH = 3cm. Găsiți zona trapezului.
10.1 Găsiți zona trapezoidului, ale cărui laturi sunt 16, 13, 6 și 13 cm.
10.2 Găsiți zona trapezului, ale cărei laturi sunt egale cu 17, 10, 5 și 10 cm.
Găsiți zona unui triunghi dreptunghi cu picioarele de 2 și 4 cm.
11.2 Găsiți zona unui triunghi dreptunghiular cu picioarele de 3 și 5 cm.
12.1 Găsiți zona unui triunghi dreptunghiular al cărui hipotensie este de 25 cm, iar unul din picioare este de 20 cm.
12.2 Găsiți zona unui triunghi dreptunghiular al cărui hipotensie este de 17 cm, iar unul din picioare este de 8 cm.
13.1 Găsiți zona unui pătrat a cărui diagonală este de 4 cm.
13.2 Găsiți zona unui pătrat a cărui diagonală este de 6 cm.
14.1 Găsiți zona unui triunghi drept. a cărei ipoteză este de 12 cm, iar unul dintre colțurile ascuțite este.
15.1 Găsiți zona unui triunghi în unghi drept. a cărei ipoteză este de 16 cm, iar unul dintre unghiurile acute este egal.
16.1 În dreptunghiular Δ ABC. - linie dreaptă, AB =, AC = 3, BC = 6. Găsiți sinA, cosA, tgA.
16.2 În dreptunghiular Δ ABC. - linie dreaptă, AB =, AC = 4, BC =.
Completați tabelul:
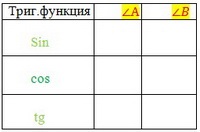
17.1 În dreptunghiular Δ ABC. ∠C este o linie dreaptă, AB = 6, ∠B =. Găsiți AC, BC.
17.2 În dreptunghiular Δ ABC. ∠C este o linie dreaptă, CB = 6, ∠B =. Găsiți AC, AB.
Probleme în geometrie în figuri:
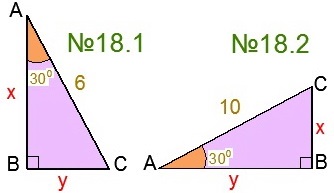
№ 18-19 Găsiți laturile lui X și Y în funcție de imagine (sarcina din stânga este tratată împreună de tutorele matematicii, iar cea dreaptă este destinată temelor)
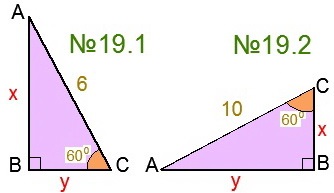
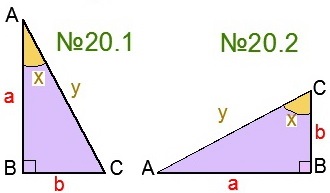
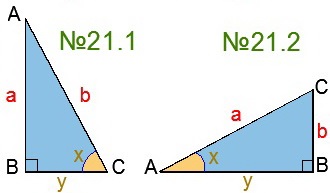
№20-21 Exprimați prin părțile X și Y a și b și b (sarcina din stânga este tratată împreună cu tutorele matematicii împreună, iar dreapta este concepută pentru teme)
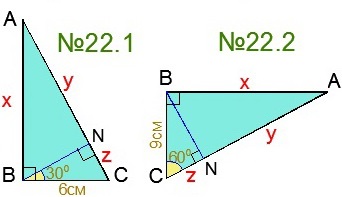
№22 Găsiți lungimile segmentelor X, Y și Z conform figurii.
Cu stimă, proprietarul site-ului Alexander Kolpakov,
tutor în matematică la Moscova.
Tutor în matematică în Strogino, m. Schukinskaya.