2.25. S-au împărțit convoluții
In multe probleme practice au nevoie pentru a calcula convoluția a două secvențe finite, atunci când unul dintre ei este mult mai lungă decât cealaltă (de exemplu, sau). Desigur, puteți alege întotdeauna egal, dar această abordare este ineficientă și din mai multe motive este incomodă. Mai întâi, înainte de a calcula convoluția, trebuie să aveți o secvență mai lungă. În practică, de exemplu în radar sau în procesarea semnalelor de vorbire, această condiție nu este întotdeauna fezabilă. În al doilea rând, deoarece procesarea începe numai după primirea întregii secvențe, rezultatul este obținut cu o întârziere mare. În cele din urmă, dacă DFT este prea mare, calculul DFT devine mult mai complicat, deoarece necesită o cantitate mare de memorie și alte dificultăți pur practice asociate cu algoritmii FFT. Următoarele două metode de calcul al convoluției nu conțin deficiențele de mai sus. Ele se bazează pe împărțirea unei secvențe mai lungi pe secțiuni și pe calcularea convoluțiilor parțiale, din care se formează secvența de ieșire dorită.
Prima dintre acestea se numește metoda de suprapunere cu sumare. Esența acestei metode este ilustrată în fig. 2.32. Pentru simplitate, presupunem că secvența nu este limitată, ci conține contează. Împărțim secvența în secțiuni adiacente de lungime de probele (Figura 2.32). Alegerea este destul de complicată, dar rezultate bune sunt obținute dacă este de aceeași ordine de mărime. Deci, secvența de intrare este reprezentată ca
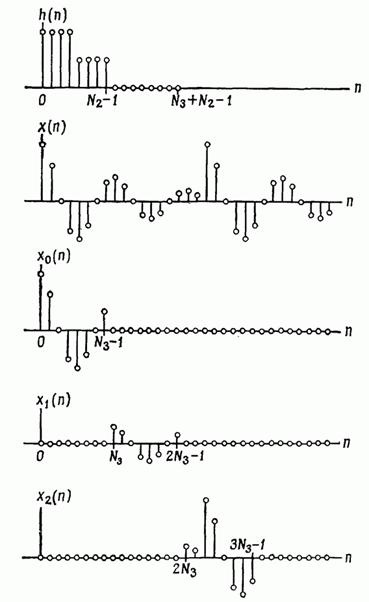
FIG. 2.32. Metoda suprapus cu sumare.
Convoluția liniară a secvențelor este egală cu
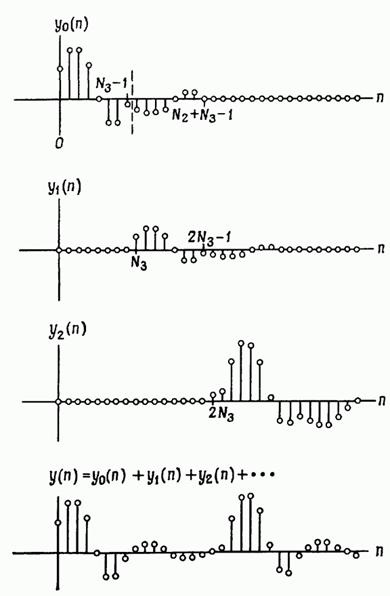
FIG. 2.33. Formarea valorilor de ieșire ale convoluției utilizând metoda de suprapunere cu sumare.
Lungimea fiecărei suma convoluție parțială (2.169) este egal cu numărul de, t. E. Există o lungime teren în probele în care se suprapun -lea și -lea sinuozitate parțiale, astfel încât citirile lor la porțiunea de suprapunere a plia. În Fig. 2.33 arată cum sunt aranjate și rezumate convoluțiile parțiale învecinate. Fiecare dintre ele este calculată prin metoda de convoluție rapidă descrisă în Sec. 2,24. Această metodă a fost numită metoda de suprapunere cu sumare tocmai pentru că se suprapun între ele convoluțiile parțiale intermediare și ele trebuie adăugate pentru a obține rezultatul final.
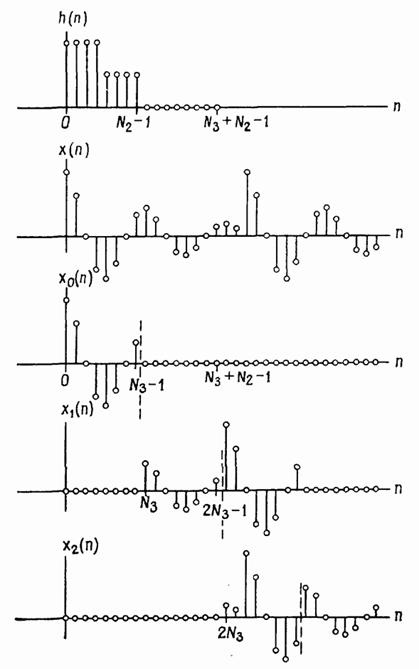
FIG. 2.34. Metoda de suprapunere a acumulării.
O altă metodă de calcul convoluția liniară a secvențelor, dintre care unul este semnificativ mai lungă decât cealaltă, de asemenea, bazat pe partiționarea unei secvențe mai lungi. Se numește metoda de suprapunere cu acumulare, iar în acest caz secțiunile de intrare, mai degrabă decât secțiunile de ieșire, se suprapun. Conținutul erratic al convoluțiilor circulare ale secțiunilor individuale este eliminat. Restul de conturi se acumulează și rezultatul final se formează din ele. Luați în considerare un exemplu specific (Figura 2.34). Secvența conține mostre, iar secvența este împărțită în secțiuni ale lungimii eșantionului, suprapuse între ele în secțiuni cu o lungime de eșantioane. (Rețineți că porțiunea de suprapunere este la capătul secvenței. Este convenabil pentru a calcula convoluția circulară folosind DFT.)
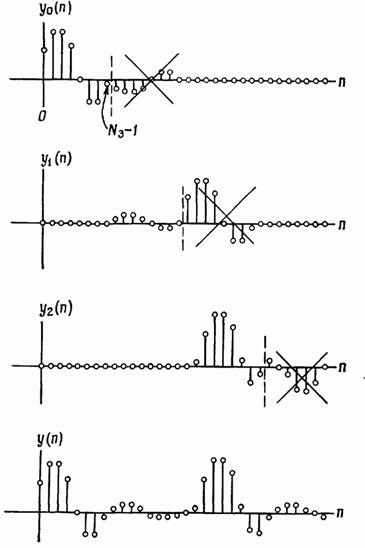
FIG. 2.35. Formarea valorilor de ieșire ale convoluției utilizând metoda de suprapunere cu acumulare.
Pentru fiecare secțiune, se calculează o convoluție circulară a secvențelor și o contorizare. Ca rezultat, un set de secvențe arătate în fig. 2.35. mostre recente din fiecare dintre secvențele eliminate (acestea sunt incorecte datorită naturii ciclice a convoluție) iar restul sunt atașate la secvența corectă contează și t. D. Rezultatul este o convoluție identitate de secvență dorită. Astfel, folosind metoda de suprapunere-adăuga sau se suprapun cu metoda de acumulare, este relativ ușor de a găsi convoluție secvențelor lungi și foarte scurte, rezultatul este obținut sub forma unor secțiuni individuale mici, care sunt unite în mod adecvat într-o singură secvență.