În triunghiul dintre laturile și unghiurile sale, există anumite relații. Dacă un colț al triunghiului este mai mare decât celălalt, atunci opusul acestuia este o latură cu o lungime mai lungă decât cea opusă celeilalte. Cu alte cuvinte, opus celui mai mare unghi al triunghiului este cea mai mare parte, vizavi de unghiul de mijloc este partea mijlocie, iar cel mai mic colț este opus celui mai mic colț.
Este clar că dacă unghiurile unui triunghi sunt egale, atunci părțile opuse față de care se află sunt egale.
Pentru a formula teorema privind raportul dintre laturile și unghiurile unui triunghi, putem folosi următoarele: în triunghiul opus unghiului mai mare se află partea mai mare. Cu toate acestea, putem formula contrariul: în triunghiul opus laturii mai mari se află un unghi mai mare.
Într-o teoremă directă cunoaștem dimensiunile unghiurilor, și de aici facem o declarație despre mărimea laturilor. Și în teorema inversă, dimensiunile laturilor sunt cunoscute și se trage o concluzie cu privire la dimensiunile unghiurilor. Aceasta înseamnă că, în demonstrarea unei teoreme directe, avem o corelație de unghiuri și este necesar să dovedim raportul de aspect. Pentru a dovedi inversul - având în vedere raportul de aspect, este necesar să se demonstreze corelarea unghiurilor.
Să dovedim o teoremă directă. Fie ca în ΔABC unghiul A să fie mai mic decât unghiul B (∠A <∠B, или ∠BAC <∠ABC). Требуется доказать, что сторона, лежащая напротив ∠A, меньше, чем сторона, лежащая напротив ∠B.
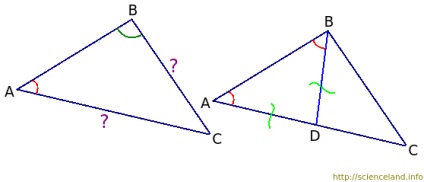
Spre deosebire de ∠A se află partea BC, iar față de ∠B se află partea laterală de curent alternativ. Este necesar să se dovedească faptul că BC În interiorul ∠B din partea AB, am pus deoparte un unghi egal cu ∠A. Este clar că acest unghi va fi mai mic decât ∠B al triunghiului ABC, deoarece prin ipoteza ∠A <∠B. Мы откладывали новый угол внутри ∠B, а значит полученная сторона нового угла пройдет внутри ∠B и пересечет сторону AC в некой точке. Назовем эту точку D. Таким образом, мы получили ∠ABD, который равен ∠A. Deoarece ∠A = ∠ABD, atunci ΔABD este isoscele. Latura lui AD este egală cu partea BD. Partea AC este formată din două segmente - AD și CD: AC = AD + CD. Dar din moment ce AD = BD putem scrie că AC = BD + CD. Acum ia în considerare ΔBCD. În ea, BD și CD sunt două fețe. Partea terță este BC. După cum se știe din teorema inegalității triunghiului, oricare dintre laturile sale este mai mică decât suma celorlalte două. Adică, BC De aici BC