Caracteristicile tipice ale modelelor de transport sunt: 1) prezența a cel puțin două puncte de livrare inițiale; 2) prezența a cel puțin două puncte finale de consum; 3) de la fiecare punct sursă, la fiecare punct final se livrează produse omogene - bice, sortimente, cherestea etc. 4) cantitățile care caracterizează volumul de produse furnizate din fiecare punct sursă sunt cunoscute sau pot fi determinate - capacitatea de expediere a fiecărui articol sursă; 5) volumul de produse consumate la fiecare destinație este cunoscut sau poate fi determinat - capacitatea de a accepta fiecare punct de consum; 6) se cunoaște sau se poate determina costul (costul) sau profitul transportului unei unități de producție de la fiecare punct sursă la fiecare punct de consum.
Scopul este atins problema de transport - definirea numărului de produse care trebuie să fie transportate de la fiecare punct de plecare în fiecare destinație și în cazul în care costurile de transport vor fi minime sau de profit (în probleme liniarizate) de transport va fi maxim. Care este obiectivul - minimizarea costurilor de transport sau maximizarea profiturilor - este și alegerea criteriului. În Fig. Figura 5.18 prezintă un model de transport sub forma unei rețele cu puncte de plecare m și n puncte de destinație. Punctele de plecare și destinații corespund nodurilor (cercuri) și a rutelor de transport - arc (linii drepte). Cantitatea de produse expediate (produse) la fiecare punct i. se desemnează prin ai și consumat (stocat) în fiecare punct j de bj; sij - costul transportului unei unități de ieșire din fiecare punct sursă i către fiecare destinație j.
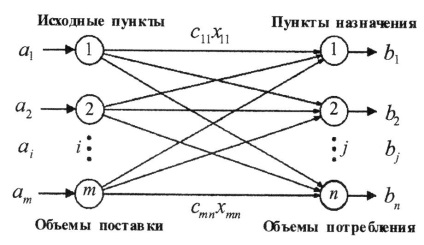
Fig. 5.18. Reprezentarea schematică a modelului de transport
Indicăm prin xij - cantitatea de producție (volume), transportată de la punctul inițial i până la destinația j. Apoi, problema tipului de transport LP în formă generală este formulată după cum urmează:
pentru a minimiza y = (5-13)
sub constrângerile = (5.14)
volumul total de transport din fiecare punct i nu poate fi mai mare decât cel disponibil:
volumul total de transport în fiecare element j trebuie să fie cel puțin egal cu cererea acestui articol:
xiji = j =. (5.16)
Dacă volumul total al punctelor sursă (furnizori) este egal cu volumul total de puncte de consum (consumatori), # 931; ai = # 931; bj. atunci modelul se numește un model de transport echilibrat.
În situațiile reale de producție, condiția menționată nu este respectată întotdeauna - volumul de aprovizionare este egal cu volumul de consum. Prin urmare, pentru a simplifica procesul de luare a deciziei, modelul de transport conduce în mod artificial la unul echilibrat prin introducerea de puncte de intrare fictive sau destinații fictive. În acest caz, în expresia constrângerilor (5.14) - cu introducerea unui punct inițial fictiv - sau (5.15) - cu introducerea unui punct fictiv de consum - se fac adăugări corespunzătoare. Costul transportului de la o sursă fictivă la puncte de consum fictive se presupune a fi zero.
15. Planul de sprijin pentru sarcina de transport
Metoda unghiului nord-vest
Lăsați condițiile de problemă de transport să fie date în tabelul 2.3. Metoda costului minim Metoda constă în faptul că toate valorile celui mai mic tabel este selectat, iar celula, ceea ce îi corespunde, este plasat la un număr minim de ai. sau bj. Apoi, elimina din luarea în considerare orice șir care corespunde vânzătorului, care își rezervă complet consumate sau coloana corespunzătoare utilizatorului ale cărui nevoi sunt pe deplin satisfăcute, sau ambele rândul și coloana, în cazul în care sunt îndeplinite rezervele de furnizor consumate și nevoile consumatorilor. Din partea rămasă a tabelului valori mai mic cost este selectat din nou, iar procesul de alocare de inventar este continuat până când toate stocul nu vor fi distribuite, iar nevoile îndeplinite. Metoda de aproximare Vogel Această metodă constă în următoarele: 1. la fiecare iterație găsiți diferențele dintre cele două cele mai mici tarife din toate rândurile și coloanele, scriându-le într-o coloană suplimentară și un rând din tabel; 2. Găsiți valoarea maximă # C16 și umpleți celula cu valoarea minimă în rândul (coloana) la care această diferență corespunde. Procesul continuă până când toate bunurile sunt transportate de consumatori. Această metodă conduce la un plan optim într-o serie de probleme. Să rezolvăm această metodă cu problema din Exemplul 2.6.1 (a se vedea tabelul 2.7). Metoda de preferință dublă Dacă tabelul de valori este mare, atunci căutarea tuturor elementelor este dificilă. În acest caz, se folosește metoda dublei preferințe, a cărei esență este după cum urmează.
Fără a lua în considerare costul transportului unității de marfă, începem să satisfacem nevoile primului consumator B1 datorită stocului furnizorului A1. Pentru aceasta, vom compara a1 = 100 sbi = 200, a1
Să compunem cu ajutorul acestei metode un plan de bază al problemei deja luate în considerare. Se scrie starea în tabel (tabelul 2.5). Alegem cel mai mic cost din tabel (acesta este costul plasat în celula A1, B4), deoarece A1 = b4. 100 de unități. Am plasat încărcătura în această celulă și excludem din considerație primul rând și a patra coloană. În tabelul rămas de valori, cel mai mic cost este localizat în celula A2. B1 și în celula A3. B5. Completăm oricare dintre ele, de exemplu A2. B1. Avem 200 <250 . следовательно, записываем в нее 200 и исключаем из рассмотрения столбец B1 . В клетку A3. B5 записываем 200 ед. и исключаем из рассмотрения строку A3 . В оставшейся таблице стоимостей снова выбираем наименьшую стоимость и продолжаем процесс до тех пор, пока все запасы не будут распределены, а потребности удовлетворены. В результате получен план
X = X14 = 100, X21 = 200, X22 = 50, X35 = 200, X42 = 150, X43 = 100, X45 =
valorile rămase ale variabilelor sunt zero.
În fiecare coloană celulă cel mai puțin valoroasă este marcată cu semnul V. Apoi, același lucru se face în fiecare linie. Ca rezultat, unele celule au marcajul VV. În ele există un cost minim, atât pe o coloană, cât și pe o linie. Aceste celule sunt plasate în volumele maxime posibile de trafic, excluzând de fiecare dată din considerente coloanele sau rândurile corespunzătoare. Apoi transportul este distribuit celulelor marcate cu semnul V. În restul mesei, transportul este distribuit la cel mai mic cost.Articole similare