În ultimul articol "Exponent și numărul e: bani ca exemplu", am analizat situația în care banii cresc exponențial și se dublează pe o anumită perioadă de timp.
Acum, să vedem cum ne schimbă înțelegerea esenței numărului e și ce să facem cu sistemele care cresc exponențial, dar nu se dublează, ci au un factor de creștere diferit.
Și ce înseamnă asta?
Numărul e (2.718) este rezultatul maxim posibil cu distribuția de creștere de 100% pentru o perioadă de timp. Desigur, am început, așteptând o creștere de la 1 la 2 (aceasta este o creștere de 100%, nu?). Dar, cu fiecare pas înainte, primim mici "dividende", care încep să crească singure. Când totul este spus și terminat, la sfârșitul unei perioade de timp avem e (2.718 ...), nu 2. Numărul e este maximul care se întâmplă atunci când se împarte 100% în cele mai mici decalaje.
Deci, dacă începem cu 1 ruble și descompunem continuu 100% din creștere, obținem 1e. Dacă luați 2 ruble ca suma inițială, veți termina cu 2e. Dacă începem cu 11.79 ruble, obținem 11.79 e.
Numărul e este ceva de genul unei limite de viteză (ca "numărul c" este viteza luminii). Această constanță arată cât de repede puteți crește folosind un proces continuu. Este posibil să nu atingeți întotdeauna limita de viteză, dar acesta este un punct de comparație convenabil: puteți descrie orice factor de creștere cu această constantă universală.
(Digresiune: feriți-vă, în care conceptul de creștere a rezultatului final al conceptului 1, devenind e (2,718 ...), a crescut (factor de creștere) la 171,8% Numărul e, în sine, este rezultatul final pe care îl vedeți după .. toate creșterile sunt creditate (suma inițială + creșterea)).
Și pot exista alți coeficienți?
Aceasta este o întrebare bună. Ce se întâmplă dacă creșterea anuală este de 50%, nu de 100%? Putem încă utiliza numărul e?
Să verificăm. Raportul de creștere compozit de 50% arată astfel:
Hmm ... Ce putem face aici? Amintiți-vă că 50% reprezintă procentajul total al venitului și n este numărul de perioade pentru care acest procent este împărțit pentru acumulare (capitalizare). Dacă alegem n = 50, creșterea noastră va fi împărțită în 50 de bucăți de 1%:
(1 + 0,50 / 50) 50 = (1 + 0,01) 50
Acest lucru, desigur, nu este infinit, ci încă un exemplu foarte detaliat. Acum imaginați-vă că am împărțit, de asemenea, creșterea noastră "normală" de 100% în bucăți de 1%:
numărul e ≈ (1 + 1,00 / 100) 100 = (1 + 0,01) 100
Ei bine, ceva este deja discernut. În cazul obișnuit, obținem 100 de modificări incrementale, câte 1% fiecare. În cazul a 50%, avem 50 de modificări incrementale de câte 1% fiecare.
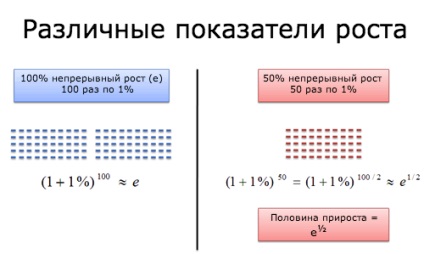
Care este diferența dintre aceste două numere? De fapt, în cazul a 50% este jumătate din caz cu 100%:
(1 + 0,01) 50 = (1 + 0,01) 100/2 = ((1 + 0,01) 100) 1/2 = e 1/2
Acest lucru este foarte interesant. 50/100 = 0,5, ceea ce este un indiciu al măsurii în care noi construim e Acesta este un principiu general. În cazul în care creșterea noastră procent a fost de 300%, am putea împărți în 300 de bucăți până la 1%. Și în cele din urmă am obține un rezultat egal cu e 3.
Având în vedere că creșterea arată ca o simplă adăugare (+ 1%), trebuie să vă amintiți că, de fapt, aceasta este o multiplicare (× 1.01). Iată de ce folosim grade (multiplicare repetată) și rădăcini pătrate (e ^ 1/2 înseamnă "jumătate" numărul de modificări, adică jumătate din numărul de multiplicări).
Deși am ales 1%, un număr mai mic (0,1%, 0,0001% sau chiar un număr infinit de mic!) Ar putea fi considerat factorul de creștere. Concluzia este că indiferent de factorul pe care îl alegem, înseamnă pur și simplu o nouă putere pentru e:
raportul de creștere = e
Și ce alte perioade de timp?
Să presupunem că vom crește cu 300% în 2 ani. Noi multiplicăm creșterea anuală (e 3) de către noi înșine:
creștere = (e 3) 2 = e 6
Gradurile magice pot evita erecția dublă. Pur și simplu se multiplică coeficientul în funcție de timp și noi ridicăm numărul e la puterea rezultată.
Secret: numărul e combină creșterea și timpul
Este uimitor! e x poate însemna două lucruri:
- x - numărul de multiplicări ale factorului de creștere: o creștere de 100% timp de 3 ani va fi e 3
- x este factorul de creștere per se: o creștere de 300% pentru un an va fi e 3.
Nu o să facă asta? Formula noastră se va rupe, nu va veni sfârșitul lumii?
Nu, totul va fi bine. Când scriem:
variabila x este o combinație a ratei de creștere și a timpului.
Permiteți-mi să vă explic. Într-o situație cu creștere continuă compusă, 10 ani cu o creștere de 3% vor da același rezultat cu 1 an cu o creștere de 30% (fără o creștere ulterioară).
- 10 ani 3% creștere va însemna că suma se va schimba de 30 de ori cu 1 la sută. Aceste schimbări apar la fiecare 10 ani, astfel încât în fiecare an suma crește cu 3%.
- 1 perioadă cu o creștere de 30% înseamnă, de asemenea, de 30 de ori 1%, dar se întâmplă tot în 1 an. Astfel, creșterea totală este de 30%, iar acest lucru se încheie.
În orice caz, există 30 de creșteri de 1% fiecare. Cu cât este mai mare rata (30%), cu atât mai puțin va dura până la aceeași valoare a profitului (1 an). Cu cât coeficientul este mai mic (3%), cu atât va dura mai mult (10 ani).
Dar, în ambele cazuri, creșterea va fi de 0,30 = 1,35 în total. Din cauza lipsei de răbdare, preferăm o creștere mai mare și mai rapidă mai lentă și mai lungă, dar numărul e arată că efectul este același în ambele cazuri.
Aici avem o formulă generală:
creștere = e x = e increment × timp
Dacă pentru o perioadă B obținem un câștig de P, creșterea noastră totală compusă va fi egală cu e nv. Apropo, funcționează și pentru creșteri negative și fracționare.
În următorul articol, luăm în considerare creșterea exponențială și numărul e pe exemple reale: creșterea cristalului, rata maximă a bancului și rata degradării radioactive.