Numerele i și j formează o inversiune în permutare. dacă i> j, dar i este localizat înainte de j. Dacă numărul de inversiuni în permutare este egal, atunci permutarea este numită chiar. altfel este ciudat. De exemplu, permutarea (4 7 1 5 3 6 2) este uniformă, deoarece numărul de inversiuni în ea este egal. Pentru a determina numărul de inversiuni într-o permutare, alegeți ordinea în care acestea sunt contorizate. Cel mai simplu mod de a calcula câte inversiuni formează un număr cu următoarele numere de permutare:
Inv (4 7 1 5 3 6 2) = 3 + 5 + 0 + 2 + 1 + 1 + 0 = 12.
Operația de transpunere constă în schimbarea a două elemente ale permutării.
Teorema. O transpunere modifică paritatea permutării la cea opusă.
Dovada. Teorema este evidentă dacă operațiile de transpunere sunt supuse la două numere de permutare adiacente. Acum permiteți să fie numere între numerele i și j. Pentru ca numărul j să fie în poziția i, trebuie schimbat cu s + 1 de vecinătate. Și apoi numărul i ar trebui să ia locul numărului j, ar trebui să fie schimbat cu vremurile vecine. În total, este necesar să se efectueze o operație de transpunere peste numerele învecinate s + 1 + s = 2s + 1 câte un număr impar. În consecință, paritatea permutației se modifică la cea opusă. # 9632;
O cartografiere unu-la-unu a unui set de elemente n pe ea însăși se numește o permutare a puterii n. În general, substituțiile sunt scrise în formularul de mai jos
Aici lucrăm, așa cum se întâmplă adesea în combinatorie, nu cu elementele unui set, ci cu numerele lor. În linia superioară-numărătorul sunt elementele setului, iar în linia de jos-numitor sunt acele elemente în care elementele numerotare corespunzătoare trec sub maparea f, Desigur, elementele numerotatorului pot fi aranjate într-o ordine diferită de cele naturale. Aici substituția este scrisă în forma canonică, când ordinea numerelor în numărător este naturală. Atât în numerotator, cât și în numitorul substituției există permutări ale puterii n. Dacă suma inversiilor în numărător și numitor este egală, substituția este numită chiar. altfel este ciudat. Pentru orice înlocuire a coloanelor de substituție, paritatea sa nu se schimbă. Pentru înregistrarea canonică a substituției
Setul tuturor permutărilor puterii n este indicat de. Numărul tuturor înlocuirilor n-etapei este n !. Introducem pe S o operație de multiplicare, compoziția mapărilor. Exemplu de multiplicare a substituțiilor:
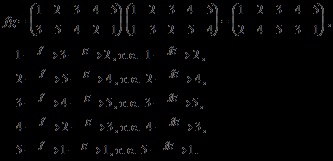
Teorema. Setul de toate permutările puterii n-a formează un grup cu privire la funcționarea compoziției mapărilor.
Pentru dovada este necesar să se verifice îndeplinirea tuturor axiomelor grupului. # 9632;
Elementul neutru este harta de identitate
Elementul invers pentru substituție este substituția