Construieste tevi de tip ZD.
Printre aceste funcții, trebuie remarcat faptul în primul rând un mijloc de trasarea unui număr de noi tipuri (de exemplu, sub forma unei linii de nivel egal, câmpuri vectoriale, etc.), precum și un mijloc de a integra grafice diferite într-una singură. De interes special sunt primele două funcții care permit de recuperare (animație) ca grafice bidimensional (însuflețite), și tri-dimensională (animate3d). Acest pachet este destul
merită să fie descris într-o carte separată. Dar, având în vedere volumul limitat al acestei cărți, vom lua în considerare doar câteva exemple caracteristice ale aplicării sale. Rețineți că pentru a utiliza aceste funcții, aveți nevoie de un apel pachet, de exemplu, cu comanda (cu).
13.6.2. Construirea grafurilor de funcții într-un sistem de coordonate polar bidimensional
În pachetul de parcele există o funcție pentru plotarea grafurilor în sistemul de coordonate polare. Are forma unui polarplot (L, o), unde L sunt obiecte pentru specificarea unei funcții a cărei grafic este reprezentat grafic și o sunt opțiuni opționale. În Fig. Figura 13.27 prezintă un exemplu de plotare cu funcția polarplot.
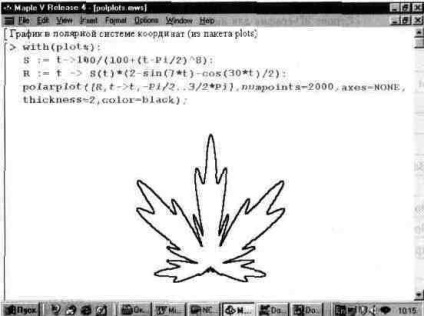
Fig. 13.27. Un grafic construit folosind funcția polarplot.
În acest caz, pentru o expresivitate mai mare, construcția axelor de coordonate este omisă, iar graficul este dedus printr-o linie de grosime dublată. Graficul este foarte asemănător cu o frunză de arțar, foarte venerată în Canada și a devenit emblema sistemului Maple V.
13.6.3. Plotarea liniilor cu niveluri egale
Graficele construite folosind linii de nivel egal (numite și grafuri de contur) sunt adesea folosite în cartografie. Aceste grafice sunt obținute prin tragere conceptual, o suprafață tridimensională peste un număr de planuri egal distanțate paralele cu planul format de axele X și Y ale graficului. Linii de înălțime egală se formează ca rezultat al intersecției acestor planuri cu o suprafață tridimensională.
Pentru a construi astfel de grafice, se folosește funcția contourplot, care poate fi folosită în mai multe formate:
conturplot ([exprf, exprg, expr], s = a..b, t = c..d)
conturplot ([f, g, h], a..b, c..d)
contourplot3d ([exprf, exprg, exprh], s = a..b, t = c..d) » '
contourplot3d ([f, g, h], a..b, c..d)
Aici - f, g și h - funcții, expri - o expresie care descrie dependența înălțimii suprafeței coordonatele x și y, exprf, exprg și exprh - expresie, în funcție de s și t, și să descrie suprafața în formă parametrică, dar, de asemenea, b - materialul constant tip, end - expresie de tip constant sau reale, x, y ,, s și t - numele variabilelor independente.
În Fig. 13.28 prezintă plotarea unui grafic cu linii de nivel egal pentru o singură funcție. Opțiunea filled = true oferă o colorare funcțională automată a formelor închise formate din linii de nivel egal. Uneori, grafica oferă mai multă expresivitate decât atunci când construiește numai linii de același nivel.
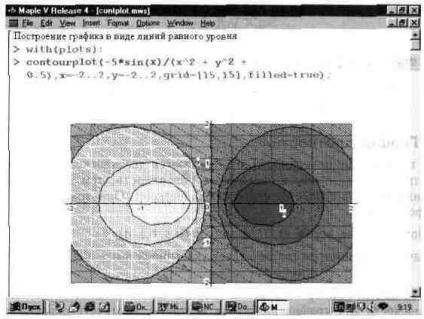
Fig. 13.28. Un exemplu de plotare a unui grafic de funcții cu linii de nivel egal.
Funcția contourplot vă permite să construiți și să creați grafice ale unui număr de funcții. Un exemplu de astfel de construcție este prezentat în Fig. 13.29. Setul de cercuri din această figură este creat de patru suprafețe definite de funcțiile c1, c2, c3 și c4.
Trebuie remarcat faptul că, deși grafica în formă de linii de nivel egal nu arata estetic plăcut și natural ca de obicei grafice suprafețelor tridimensionale (pentru necesită interpretarea rezultatelor), ele au un avantaj important - extremele funcțiilor pe aceste grafice arată, uneori, mai clar decât hărți convenționale. De exemplu, un mic deal sau jgheab pentru mare „munte“ pe un grafic convențional poate fi invizibil, deoarece ascuns
"Munte" - pe harta liniilor de același nivel acest efect nu este prezent. Cu toate acestea, expresivitatea acestor grafice depinde foarte mult de numărul de linii de nivel egal.
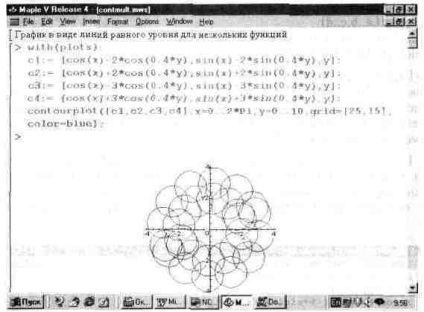
Fig. 13.29. Un exemplu de plotare a grafurilor mai multor funcții de linii de nivel egal.
13.6.4. Graficul densității
Uneori, suprafețele tridimensionale sunt afișate în plan ca grafică a densității de culoare - cu cât este mai înaltă înălțimea suprafeței, cu atât culoarea este mai densă. Acest tip de grafice este creat de funcția densityplot. Acesta poate fi înregistrat în două formate:
unde alocarea parametrilor corespunde cu cea specificată mai sus pentru funcția contur-plot.
În Fig. 13.30 dat un exemplu de complot acest tip de diagramă. Nu este greu de observat că în planul X, Y graficul este împărțit în pătrate a căror densitate de culoare este diferită. În cazul nostru, densitatea de culoare este stabilită în nuanțe de gri.
De obicei, graficele de acest tip nu sunt foarte expresive, dar au propriile lor domenii de aplicare. De exemplu, nuanțele culorii unui lichid translucid pot indica relieful suprafeței fundului containerului în care este localizat acest lichid.
13.6.5. Graficul unui câmp vectorial bidimensional
Un alt mod obișnuit de reprezentare a suprafețelor tridimensionale este reprezentat de graficul unui câmp vectorial. Ele sunt adesea folosite pentru a afișa câmpuri, de exemplu, încărcături electrice. Particularitatea acestor grafice este aceea că se utilizează săgeți pentru construcția lor, direcția căreia corespunde direcției gradientului gradientului de câmp și lungimea până la valoarea gradientului.
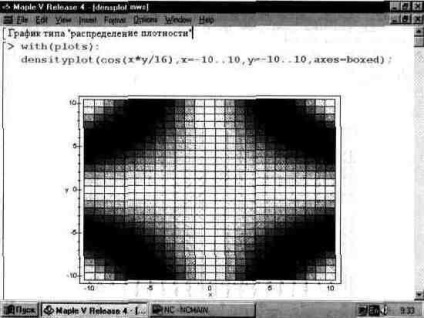
Fig. 13.30. Graficul densității pentru o funcție dată.
Pentru a construi astfel de grafice într-un sistem de coordonate bidimensional, utilizați funcția fieldplot:
domeniuplot (f, rl, r2) sau fieldplot (f, rl, r2.),
unde f este vectorul sau setul de vectori care specifică construcția și rl și r2 sunt limite.
În Fig. 13.31 este o vedere a unuia dintre astfel de grafice. Trebuie remarcat că, pentru a obține un număr suficient de săgeți distinct vizibile, trebuie să lucrați cu formatarea graficelor. În caz contrar, graficele de acest tip ar putea să nu fie foarte reprezentative. Deci, săgețile prea scurte se transformă în liniuțe și chiar în puncte care nu au un punct, ceea ce privează grafica clarității.
Puțin mai târziu vom lua în considerare construirea câmpurilor de densitate și vector într-un singur desen, precum și crearea de săgeți de grăsime mai vizibile.
13.6.6. Grafice în diferite sisteme de coordonate
În pachetul de parcele există multe funcții pentru plotarea graficelor în diferite sisteme de coordonate. Volumul cărții nu permite reproducerea exemplelor pentru toate tipurile de astfel de grafice, deoarece există multe sute dintre ele. Da, acest lucru nu este necesar - în exemplele încorporate în sistemul de ajutor, puteți găsi toate informațiile necesare. Deci limitează doar pereche exemple de funcții tubeplot (C, opțiuni), care permite de a construi o formă foarte intuitiv în spațiu seamănă cu o țeavă sau alte obiecte formate de piese de rotație.
În Fig. 13.32 una dintre aceste cifre este arătată. Seamănă în mod izbitoare cu o coajă de melc. Colorarea funcțională este realizată prin rafinarea graficului folosind bara de formatare. Semnificația parametrului C (în documentul Conchoid) este ușor de înțeles din acest exemplu.
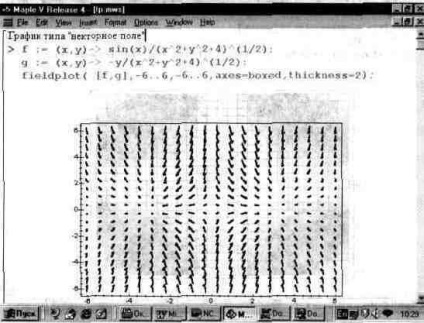
Fig. 13.31. Graficul grafic bidimensional al tipului de câmp vectorial.
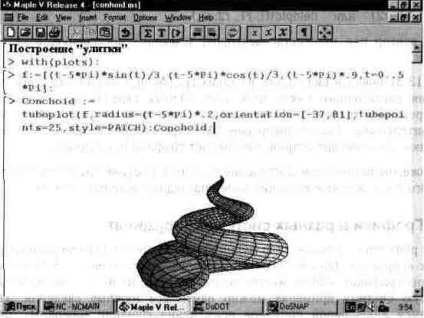
Fig. 13.32. Planificarea programului de "melc".
Această funcție poate fi, de asemenea, utilizată pentru a construi un număr de obiecte tubulare în spațiu. Aceasta stabilește automat algoritmul pentru eliminarea liniilor invizibile, chiar și pentru forme destul de complexe. Acest lucru este ilustrat printr-un exemplu
în Fig. 13.33, care arată figura "lanțului". Nu este realismul acestei cifre uimitor?
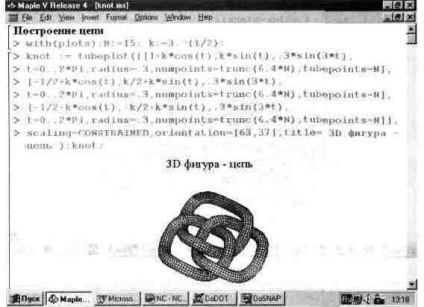
Fig. 13.33. Figura "lanț", construită folosind tubulatura funcție.
Poate fi mult să se gândească la modul în care natura „învățat“ despre legitățile matematice, care constituie baza unor obiecte geometrice, sau, poate, despre geniul poporului, care au fost în stare să găsească astfel de legi pentru obiecte naturale. În zilele noastre Maple V oferă oportunități excelente pentru astfel de oameni.
13.6.7. Graficele tipului unui câmp vectorial tridimensional
Vizibilitatea unui număr de grafice poate fi mărită substanțial prin construirea acestora într-o reprezentare tridimensională. De exemplu, pentru această construcție a câmpurilor vectoriale, puteți utiliza funcția grafică fieldplot3d. Spre deosebire de fieldplot funcția, construiește săgeți ca în spațiul tridimensional (Figura 13.34).
Tot ceea ce sa spus despre singularitățile unor astfel de grafice bidimensionale rămâne valabil pentru graficele celor tridimensionale. În special, pentru a obține o reprezentativitate suficientă, este necesar să se depaneze cu atenție formatele de prezentare ale acestor grafice.
13.6.8. Contur grafică 3D
Spre deosebire de grafică vectorială, tridimensionale parcele de contur de suprafață suprapuse pe aceste suprafețe în sine, de multe ori crește susceptibilitatea unor astfel de suprafețe - ca un linii de rama de tablou. Pentru construirea simultană a unei suprafețe tridimensionale și a liniilor de contur pe ele, funcția contourplot3d servește. Un exemplu de aplicare a acestuia este prezentat în Fig. 13.35.

Fig. 13.34. Construcția unui câmp vector în spațiul tridimensional.
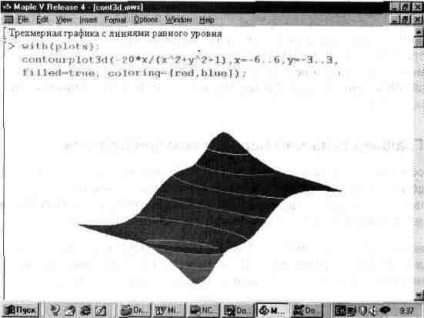
Fig. 13.35. Graficul unei suprafețe tridimensionale cu linii de contur.
Pentru a îmbunătăți vizibilitatea, acest grafic este rafinat folosind bara de instrumente pentru formatarea graficului. În particular, este inclusă colorarea funcțională și sunt selectate unghiurile de vizualizare ale figurii, la care depresia și vârful figurii sunt vizibile.
13.6.9. Tehnica de vizualizare a formelor spațiale complexe
Exemplele destul de simple de mai sus dau o idee despre gradul înalt de vizualizare a formelor geometrice folosind pachetul de parcele. Aici vom examina mai multe exemple de vizualizare a figurilor tridimensionale. Mulți au văzut inductori, în care sârma unui alt diametru este înfășurată pe un miez magnetic toroidal. AbstracŃia matematică a unei astfel de bobine este prezentată în Fig. 13.36.
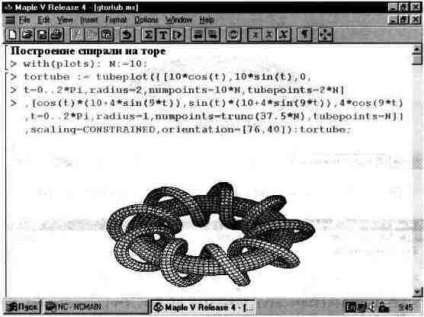
Fig. 13.36. Sus cu bobina - o spirală groasă.
În document (Figura 13.36) un număr destul de mare de parametri de opțiune sunt utilizați pentru funcția tubeplot. Nu întotdeauna efectul lor este evident. Prin urmare, în Fig. Figura 13.37 prezintă construcția a trei tori care intersectează reciproc cu diferite tipuri de construcție. Această figură oferă, de asemenea, o reprezentare vizuală a posibilității de a construi mai multe obiecte grafice (reprezentate de funcțiile p1, p2 și p3) utilizând funcția tubeplot funcție.
În mai multe cazuri, cifrele prezentate grafic pot fi construite folosind o combinație de același tip de cifre. Este prezentat un exemplu de grafic de acest fel