Calcularea unui circuit cu o sarcină asimetrică
Linia aeriana> Metoda de componente simetrice
Calcularea unui circuit cu o sarcină asimetrică
În condiții normale, regimurile asimetrice în circuitele trifazate de înaltă tensiune sunt relativ rare (în principal în lanțuri cu cuptoare cu arc electric și motoare de tracțiune monofazate). În mod obișnuit, modurile asimetrice sunt obținute în condiții de urgență, când apare asimetria în orice lanț.
Există două tipuri de asimetrie - transversale și longitudinale. Asimetria transversală într-un circuit simetric trifazat are loc cu o sarcină asimetrică. Acesta include, în special, diferite tipuri de scurtcircuite asimetrice (închideri între faze, închiderea uneia sau a două faze la masă). Asimetria longitudinală apare dacă elementele cu rezistențe inegale sau în cazul unei rupturi a unuia sau a doi fire (secțiunea neechilibrată a unei linii) sunt incluse în tăierea liniei de fază.
Pentru calcule ale modurilor asimetrice ale circuitelor trifazate, care este de a utiliza principiul compensării, receptorul înlocuind porțiunea asimetrică sau dezechilibrată în tensiunea de linie sursă (tensiune), care valorile pentru a calcula închiderea totală rămân necunoscute. Fezabilitatea acestei tehnici constă în faptul că, după un astfel de circuit de înlocuire devine simetrică și componentele sale heteronymic simetrice de curenți și tensiuni sunt independente unul față de celălalt. Legăturile dintre componentele simetrice ale curenților și tensiunile diferitelor secvențe, cauzate de asimetrie, sunt introduse mai târziu.
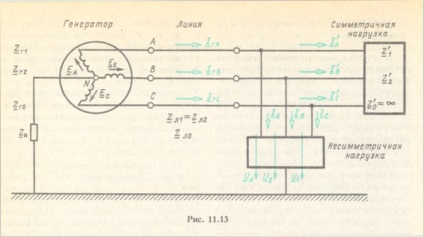
Luați în considerare metoda de calcul utilizând exemplul circuitului din Fig. 11.13, care conține încărcări statice asimetrice dinamice () și asimetrice. Lăsați emf-ul generatoarelor și rezistența elementelor de circuit. Este necesar să se găsească curenți și tensiuni. În Fig. 11.13 Circuitul și rezistența de sarcină neechilibrată nu sunt prezentate, deoarece acestea nu sunt necesare în prima etapă a calculului.
Înlocuim sarcina asimetrică cu trei surse EMF cu tensiuni necunoscute și obținem un circuit simetric care, pe lângă generatorul cu un sistem EMF simetric, conține surse cu tensiuni asimetrice.
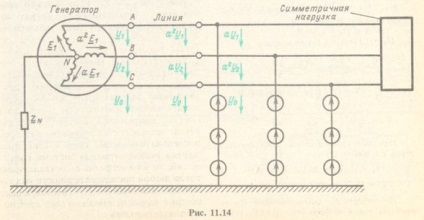
Se descompune eforturile în componente simetrice. luând faza A pentru principalul. Ca rezultat, obținem o schemă simetrică (Figura 11.14), iar în ramura în care a existat o sarcină asimetrică, există surse de trei sisteme simetrice de tensiuni de secvențe directe, inverse și zero.
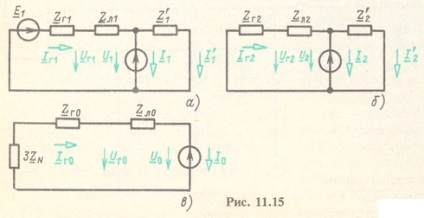
Modul de faza A a circuitului original (vezi Figura 11.13) este determinat prin suprapunerea modurilor acestor trei circuite.
Configurările schemelor secvențelor înainte și înapoi sunt întotdeauna aceleași. Schema de secvență zero este de obicei semnificativ diferită. În acest exemplu, nu are ramificație, deoarece nu pot fi curenți de secvență zero în partea dreaptă a circuitului trifazat (a se vedea figura 11.13). Trebuie acordată o atenție deosebită faptului că rezistența conductorului neutru este introdusă în circuitul secvenței zero cu o valoare triplă (vezi secțiunea).
Din considerație Mapping arată că cele mai mari valori ale componentelor simetrice de tensiuni negative și homopolar observate la locul unei conexiuni asimetrice a receptorului, așa cum în Schemele și anume există surse EMF negative și secvența zero.
Pentru calcule ulterioare, este utilă transformarea schemelor de secvențe individuale în cea mai simplă formă, fără a afecta ramurile cu surse de tensiuni necunoscute.
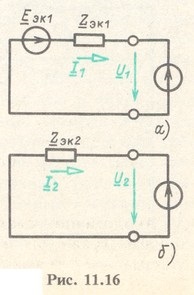
În schema de secvență inversă, combinăm ramurile generatorului și receptorul simetric (figura 11.16, b):
Schema secvenței zero în acest exemplu nu are nevoie de o conversie, deoarece are forma cea mai simplă.
Pentru fiecare dintre cele trei scheme, scriem ecuațiile conform celei de-a doua lege a lui Kirchhoff:
Există șase necunoscute în aceste trei ecuații: Cele trei ecuații suplimentare care leagă aceste șase cantități necunoscute pot fi compilate pe baza unui circuit dat și a unui parametru al unui receptor asimetric.
Fig. 11.16
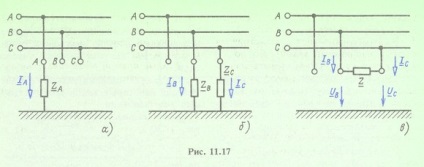
Să formăm ecuații suplimentare pentru anumite tipuri de receptoare asimetrice. Pentru receptorul prezentat în Fig. 11.17, a
Pentru receptorul prezentat în Fig. 11.17,6
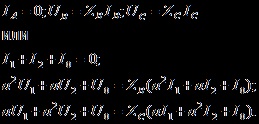
Dacă nu există o conexiune a unui receptor asimetric cu solul, de exemplu, pentru circuitul prezentat în Fig. 11.17, c, componentele simetrice ale curenților secvenței zero sunt zero și compoziția circuitului secvenței zero în etapele anterioare de calcul scade. Sunt obținute două ecuații de bază cu patru necunoscute și trebuie să se facă doar două ecuații suplimentare, și anume:
În mod analog, se formează ecuații suplimentare pentru alte tipuri de sarcină asimetrică statică. În soluția simultană a ecuațiilor lui Kirchhoff pentru schemele de secvențe diferite cu ecuații suplimentare, sunt determinate componentele simetrice ale curentului fazei A dintr-o ramificație la un receptor asimetric. Apoi distribuția acestor componente este determinată de ramificațiile individuale ale schemelor secvențelor directe, reciproce și zero. Cunoscând componentele actuale din orice ramură, calculați curentul efectiv în fiecare fază și componentele picăturilor de tensiune ale diferitelor secvențe și apoi tensiunile de fază din secțiunile individuale ale circuitului.
Să dăm un calcul al regimului circuitului (vezi Figura 11.13) pentru cazul unei sarcini asimetrice, prezentată în Fig. 11.17, cu condiția ca (defecțiune la sol monofazată). Să formuleze ecuații suplimentare
Scăderea (11.24) de la (11.23), obținem
Înlocuind acest rezultat în (11.23), avem
Le înlocuim în (11.21), apoi le adăugăm împreună și, luând în considerare (11.22), obținem
Componentele simetrice ale tensiunilor (în locul defecțiunii de pământ) sunt determinate de la (11.21):
Pentru circuitele din Fig. 11.15 și
Fig. 11.15, b
Fig. 1115, în
Componentele simetrice ale tensiunilor la bornele generatoarelor pot fi găsite prin aceleași scheme din Fig. 11.15: