Aritmetică extraordinară
Ne-am obișnuit cu operațiunile aritmetice, astfel încât să le executăm în mod automat, aproape fără să ne gândim la ceea ce facem. Dar aceleași acțiuni vor necesita mult efort din partea noastră dacă dorim să le aplicăm numerelor scrise nu în sistemul zecimal. Încercați, de exemplu, să adăugați următoarele două numere scrise pe un sistem penitențial:
Pliați în cifre, începând cu unitățile, adică pe dreapta: 3 + 2 este de 5; dar nu putem scrie 5, pentru că nu există o astfel de cifră în sistemul penitențial: 5 este deja o unitate de cea mai înaltă ordine. Prin urmare, în sumă nu există unități; scrieți 0 și 5, adică unitatea următoarei cifre, este menținută în minte. În plus, 0 + 3 = 3, și chiar unitatea reținut în minte, doar 4 unități de nivelul al doilea. În a treia cifră, obținem 2 + 1 = 3. În cel de-al patrulea 4 + 2 este 6, adică 5 + 1; scriem 1 și 5, adică unitatea din categoria cea mai înaltă, ne referim mai departe la stânga.
Suma cerută este 11340.
Am lăsat-o cititorului să verifice această adăugire prin traducerea mai întâi a numerelor în citate într-un sistem zecimal.
În același mod, se fac și alte acțiuni. Pentru exercițiu, prezentăm mai jos un număr de exemple, numărul cărora cititorul, dacă se dorește, poate crește independent:
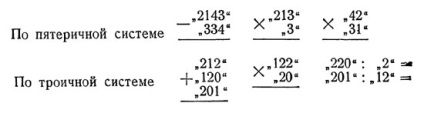
Pe sistemul pentagonal: "1304", "1144", "2402".
Atunci când efectuăm aceste acțiuni, reprezentăm în mod mental numerele scrise în sistemul zecimal obișnuit, iar după obținerea rezultatului, îl reprezentăm din nou în sistemul non-zecimal necesar. Dar puteți face același lucru: creați o "masă suplimentară" și o "tabelă de multiplicare" în aceleași sisteme în care sunt date numerele și le folosiți direct. De exemplu, tabelul de adăugare în sistemul penitențial este după cum urmează:
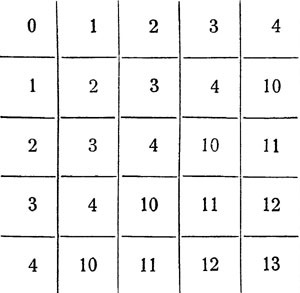
Cu ajutorul acestei tablete am putea adăuga numerele "4203" și "2132" scrise în sistemul penitențial, cu mult mai puțin accentuat decât cu metoda aplicată anterior.
De asemenea, scăderea este simplificată.
De asemenea, compunem tabelul de multiplicare ("Pythagorov" *) pentru sistemul penitenciar:
* (Pythagoras (secolul VI î.Hr.) este un filozof grec antic, el a studiat, de asemenea, matematica și teoria muzicii).
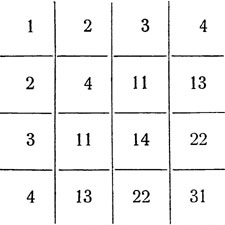
Având această placă înaintea ochilor, puteți din nou să vă ușurați să multiplicați (și să împărțiți) numerele într-un sistem pentenar, așa cum puteți vedea cu ușurință prin aplicarea acesteia la exemplele de mai sus. De exemplu, când se înmulțește
raționăm astfel: de trei ori "14" (de la masă); 4 scrie, 1 - în minte. 1 la 3 dă 3 și chiar 1, - scrie 4. De două ori trei = "11"; 1 scrie, o mutare în stânga. Avem rezultatul "1144".
Cu cât baza sistemului este mai mică, cu atât mai mici și mai potrivite sunt tabelele de adăugare și multiplicare. De exemplu, pentru un sistem ternar, ambele tabele sunt după cum urmează:
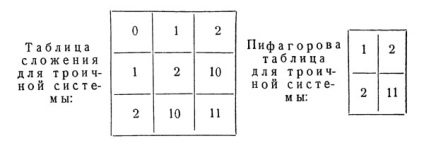
Aceștia ar putea fi imediat reținuți și folosiți pentru a efectua acțiunea. Cele mai mici tabele de adunări și scăderi sunt obținute pentru sistemul binar:
Cu ajutorul acestor "tabele" simple puteți efectua toate cele patru acțiuni în sistemul binar. Înmulțirea în acest sistem, în esență, așa cum era, nu face deloc: la urma urmei, înmulțirea cu unul înseamnă să lăsăm numărul neschimbat; Înmulțirea cu "10", "100", "1000" (adică cu 2, 4, cu 8) se reduce la simpla atribuire a numărului corespunzător de zerouri la dreapta. În ceea ce privește adăugarea, pentru ao implementa, trebuie doar să vă amintiți că în sistemul binar 1 + 1 == 10. Nu este adevărat că am numit pe bună dreptate sistemul binar cel mai simplu dintre toate posibil? Lungimea numerelor acestei aritmetici specifice este răscumpărată de simplitatea efectuării tuturor operațiunilor aritmetice asupra lor. Să fie necesar, de exemplu, să se înmulțească:
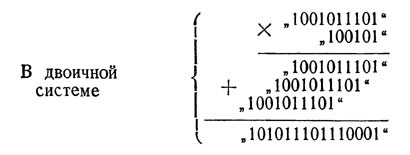
Executarea unei acțiuni este redusă doar la rescrierea numerelor lungi în aranjamentul potrivit: acest lucru necesită un efort mental incomparabil mai mic decât înmulțirea acelorași numere în sistemul zecimal (605 X X37 = 22385).
Dacă am fi adoptat un sistem binar, studiul calculului scris ar necesita cea mai mică presiune de gândire (dar cea mai mare cantitate de hârtie și cerneală). Cu toate acestea, într-un cont oral, aritmetica binară este mult inferioară celei zecimale pentru confortul efectuării acțiunilor.
De asemenea, oferim un eșantion de funcționare a diviziunii efectuate în sistemul binar:
În sistemul zecimal obișnuit, această acțiune ar avea următoarea formă:
Dividendul, divizorul, coeficientul și restul sunt în esență aceleași în ambele cazuri, însă calculele intermediare sunt diferite.