H și această pagină conține teorema de geometrie plana pe care profesorul de matematică poate fi folosit în prepararea studenților capabili într-un serios examen: concurs sau examen de la Universitatea de Stat din Moscova (în curs de pregătire la Mekhmat, WFC), pentru Jocurile Olimpice de la Școala Superioară de Economie, pentru Jocurile Olimpice de la Academia de Finanțe și în MIPT. Cunoașterea acestor fapte deschide oportunități mari pentru tutor pentru a compila sarcini competitive. Mai degrabă „bate“, o parte din această teorie pe numerele sau să completeze elementele sale relații necomplicate cu alte obiecte matematice, iar rezultatul este destul de decente sarcină olimpiada. Multe dintre proprietățile sunt prezente în manuale școlare înalte ca ținte pentru dovada și nu a prezentat în mod specific titlurile și capitole de paragrafe. Am încercat să corectez acest neajuns.
Matematica este un subiect imens, iar numărul de fapte care pot fi identificate ca teoreme este infinit. Un tutore de matematică nu poate cunoaște fizic și nu-și amintește totul. Prin urmare, unele interrelații dificile între obiectele geometrice sunt deschise de fiecare dată profesorului din nou. Colectarea tuturor pe o singură pagină este imposibil fizic. Prin urmare, voi umple pagina treptat, deoarece teoremele sunt folosite în lecțiile mele.
Îi sfătuiesc să înceapă tutorii de matematică să fie mai atenți în utilizarea materialelor de referință suplimentare, deoarece cele mai multe dintre ele nu știu elevii.
Tutor în matematică asupra proprietăților formelor geometrice
1)
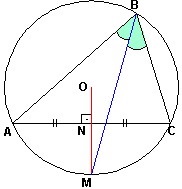
2)
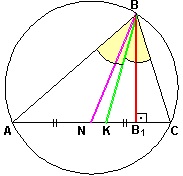
3)
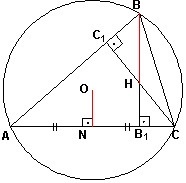
4)
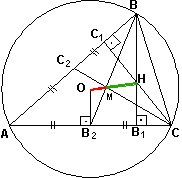
5)
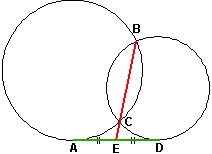
6)
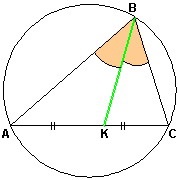
Aceasta este următoarea egalitate
7)
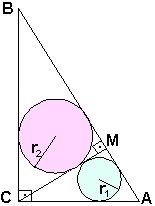
8)
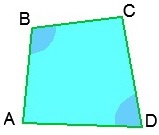
, unde x este suma oricăror două unghiuri opuse ale patrulaterului. Dacă acest patrulater este înscris într-un cerc, atunci formula ia forma:
și se numește formula Brahmagupta
9) Dacă quadrilateralul este circumscris (adică, cercul este înscris în el), atunci suprafața patrulaterală este calculată prin formula
10)
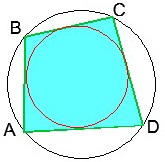
11)
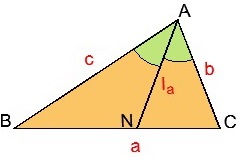
Pentru un tutore cu experiență, pentru a nu pierde calificarea, vă sfătuiesc să revizuiți în mod regulat variantele Olimpiadei, indiferent de componența studenților actuali. Mai întâi de toate, pentru a menține un nivel adecvat de dezvoltare. Uită-te la cărțile de referință și enciclopediile. Extindeți orizonturile și îmbunătățiți-vă! Pentru aceasta, această pagină este făcută!
În prezența cunoștințelor suplimentare despre fapte geometrice, tutorele matematicii va fi de mare ajutor pentru student în căutarea unor soluții rapide. De exemplu, un astfel de ajutor poate fi obținut de la mine în Strogino. În viitor, atunci când lucrați cu sarcini dens, acest lucru va conduce la o reducere a timpului pentru rezolvarea problemei C4 asupra UTI în matematică. Pe USE, puteți rezolva problema în orice mod corect, chiar și cu utilizarea instrumentelor și a proprietăților care nu sunt incluse în curriculum-ul școlar (inclusiv în matematică superioară).
Cu respect profund, Kolpakov AN
Un tutore matematic calificat. Strogino. m. Shchukinskaya. Pregătirea pentru orice fel de examinări, precum și pentru olimpiade.
Mulțumesc. Materialele site-ului sunt proiectate și accesibile și sunt adesea folosite pentru rezolvarea problemelor interne. Din păcate, locuiesc într-un alt oraș și nu există posibilitatea de a angaja un tutore. La școală dau un minim, așa că pentru mine multe dintre teoremele din această pagină nu erau familiare.
Accidentally stumbled pe site-ul. Foarte frumos, ușor, alb. M-am dus la cerere - intersecția de înălțimi.
Acum, dacă ar exista dovezi, ar fi mult mai ușor.