Smoothing spline în MathCAD
Spre deosebire de un spline interpolat. care trece prin punctul cunoscut i, fi> și deja puse în aplicare în MathCad cu ajutorul funcțiilor încorporate și cspline interp. Splinele netezite nu trebuie să treacă prin măsurători. Dar este mult mai flexibil și capabil, dacă este configurată, pentru a compensa dimensiunile „anormale“ sau pur și simplu „face pentru“ date mai bune decât OLS (sau mai precis, mai bine - o singură „explozie“ Fi nu „trage“ în sus sau în jos întreaga spline de netezire, spre deosebire de polinomul MLS cu o bază de putere).
Afirmația problemei este următoarea: să presupunem că pe grilă x1 unde h = x-xi este distanța până la cel mai apropiat nod de rețea, c3, i. c2, i. c1, i. i = 1, 2. N - 1 sunt coeficienții splinei de netezire pe intervalul i de-a lungul axei x. și yi sunt valorile splinei netezite calculate la nodurile de rețea xi. i = 1, 2. N. În general, alegerea acestor parametri este o sarcină separată. În soluția propusă, construcția unui spline de netezire se realizează utilizând două funcții. Funcția SmoothSpline (x, f, df, sm) returnează un obiect format dintr-o serie de coeficienți c ai netezirea dimensiunii spline 3 * (N-1) și valorile vectorului y ale spline de netezire grid (dimensiune N). Codul funcției de aici nu este dat din cauza volumului său - una și jumătate de pagini. Puteți vedea acest lucru descărcând fișierul atașat, dar puteți apela funcția de mai jos:

apelați funcția SmoothSpline
Rețineți că a treia dimensiune „anormal“, iar restul sunt valorile f (xi) = xi 2. Prin urmare, greutatea DF3 umflate (denumite în continuare, elementele de matrice și vectori sunt numerotate de la unul, deci fișierul MathCAD începe prin definirea unei ORIGIN variabile de sistem: = 1).
De asemenea, este indicat un mod bun (pentru valori mici de N) pentru a alege valoarea parametrului sm smootion.
Funcția răspunde la erorile din datele sursă - cum ar fi numărul de noduri de rețea mai mici de două și absența unei comenzi stricte prin creșterea valorilor lui xi.
Funcția folosește în plus numai seria reală de servicii r de dimensiune 7 * (N + 2). adică este destul de economic din memorie.
Testul și rezultatul acestuia au fost verificate împotriva materialelor Centrului de Cercetare pentru Calculul MSU, totul a coincis cu :)
A doua funcție - GetSmoothSpline (x, dx, y, c) este angajată în construcția cunoscute valorile matricei coeficientului de spline și c uniformizare în spline yi nodurile de rețea xi. argumentul x din interiorul funcției se schimbă de la x1 la xlength (x) cu pasul dx. Funcția returnează o matrice a doi vectori coloană - sunt cuprinse în prima valoare a argumentului în al doilea - valorile calculate ale spline. Utilizați funcția și apoi afișați grafic rezultatul netezerii, de exemplu, după cum urmează:
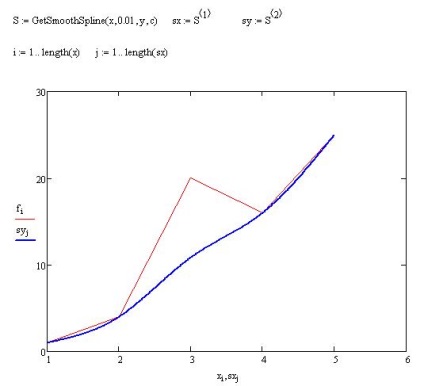
apelați funcția GetSmoothSpline
Ca un al doilea exemplu va arăta modul în care nervura netezirea este capabil să facă față cu măsurătorile „anormale“ care rezultă din activitățile dușmanii poporului oricăror eșecuri și nu se încadrează în „imaginea de ansamblu.“
Datele din acest moment vor fi generate programat, pur și simplu "eliminându-le" dintr-o bucată de sinusoid, apoi o serie de măsurători vor fi foarte diferite de celelalte:

date cu măsurători "anormale"
Iată cum splinea netezitoare cu cele două gay "evacuări" a reușit:
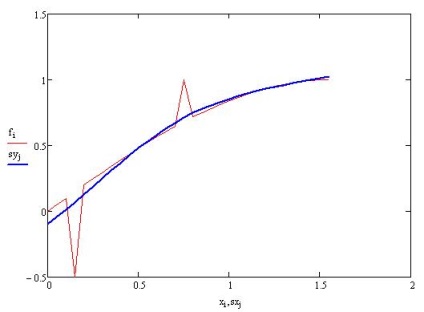
prelucrarea datelor cu măsurători anormale, spline de netezire
Se poate observa că el aproape nu a observat abaterile.
Ei bine, vreți chiar mai bine - justificați greutățile nodurilor și parametrul de netezire.
Desigur, spline de netezire nu este atotputernic - de exemplu, în cazul în care grila „peremelchit“ si exagerati cu numarul de „anomalii“, el poate merge la „Peddle“, atunci pentru prelucrarea acestor date ar trebui să implice o mașină capabilă să ia în considerare calitative a constrângerile a priori ( „, dar în acest interval funcția ar trebui să crească! "). Un astfel de dispozitiv este cunoscut sub numele de spline descriptive, dar articole despre ei, nu am scris pentru o lungă perioadă de timp, poate vreodată :)