1 matrice de programare de bază

2 Arrayuri Un array este o colecție de același tip de date (numere, simboluri, cuvinte) care sunt stocate într-o singură locație în memoria calculatorului în celule numerotate. Matricea are: - Nume - Tip (% - întreg, $ - char, unsigned - real) - dimensiunea - numărul elementelor - Index - numărul elementului Fiecare element de matrice în forma generală descrisă ca în (I), unde B - un nume de matrice I - numărul sau indexul elementului matricei

3 O matrice este un set ordonat de cantități omogene, fiecare denotată cu același nume, cu indicatori întregi întregi care variază în ordine. O matrice este o colecție de date omogene (numere, simboluri, cuvinte). Definiții de bază O matrice unidimensională O matrice bidimensională O matrice tridimensională
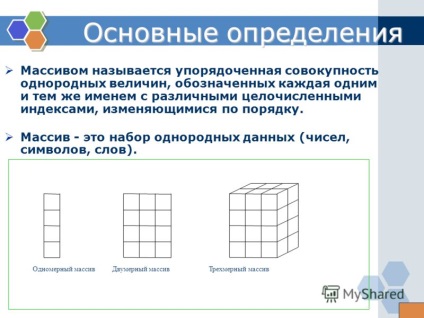
5 Matrice unidimensională Matricea unidimensională poate fi considerată ca o listă a acelorași elemente. De exemplu, lista de nume de grupuri de elevi - matrice unidimensională, date numerice privind temperatura medie pentru luna - matrice unidimensională, literele alfabetului rusesc - matrice dimensionale. În BASIC, elementele matricei sunt localizate în celule de memorie succesive. Aceasta înseamnă că matricea ocupă o zonă de memorie contiguă. Înainte de a putea accesa matricea din program, trebuie să specificăm cât de multă memorie este necesară pentru alocarea matricei. Întreaga matrice este determinată de cantitatea de memorie ocupată de un element al matricei înmulțită cu numărul de elemente din matrice. Prin urmare, trebuie să specificați numărul maxim de elemente din matrice. În descrierea companiei Microsoft dimensiunea matrice BASIC se face prin intermediul operatorului DIM, care are următoarea sintaxă: nume array DIM (numărul maxim de elemente de matrice), de exemplu: DIM S (5) Denumirea S matrice 5 numărul maxim de elemente de matrice, DIM M (25) M este numele matricei, 25 este numărul maxim de elemente din matrice.

1 Metoda iunie (a umple matrice folosind operatorul de atribuire) CLS 10 DIM S (5) Atribuirea de valori elementelor de matrice este declarat în această matrice linie numit S, iar cele cinci elemente 11 S (1) = 53 12 S (2) = 31 13 S ( 3) = - 32 în aceste rânduri elementele de matrice sunt atribuite valori de 14 S (4) = 44 15 S (5) = PRINT "S (1) este"; S (5) 17 PRINT "S (2) este egal"; S (4) 18 PRINT "S (3) este egal"; S (3) în aceste linii pe ecran secvențial 19 PRINT "S (4) este egal"; S (2) afișează valorile elementelor matricei 20 PRINT "S (5) este egal"; S (1) Rezultatul acestui program va arăta astfel:

Iulie metoda 2 (umplere array utilizând introducerea operatorului Atribuirea de valori elementelor CLS INPUT matrice Introduceți numărul de elemente de matrice; N DIM A (N) pentru I = 1 TO N Type PRINT i; array elementul INPUT A (I) NEXT I FOR I = 1 tO N PRINT a (I) NEXT I pentru rezultatele cele 3 elemente ale programului ar fi: tipul 1 array element de matrice 23 Tip 2 Tip 3 -54 element de matrice ...

3 Metoda octombrie (umplerea prin intermediul operatorului DATA array) Atribuirea elementelor DE DATE Valori CLS matrice 23, 13, 98, -8, 7 DIM M (5) pentru I = 1 TO 5 CITIRE M (I) PRINT M (I) I URMĂTORUL Rezultatele acestui program vor arăta astfel:

04 septembrie proces (umplerea matrice cu un generator de numere aleatorii) Atribuirea de valori ale elementelor de matrice DIM S (IOO) FOR i = 1 LA 100 S (i) = 1 + INT (1000 * RND) i NEXT
10 Înainte de a începe să lucrați cu matricea, trebuie să rezervați un spațiu pentru ea în memorie. Pentru aceasta, există un operator DIM (de la cuvântul englez "dimention" - volum, mărime, mărime, măsură). DIM A (10) De obicei, se spune că există un spațiu rezervat pentru 10 elemente ale matricei A, dar de fapt 11 este rezervat deoarece numerotarea celulelor începe la 0. Dar, deoarece suntem mai obișnuiți să începem numărarea cu 1, prima celulă ("zero") nu este pur și simplu utilizată. Metode de umplere matrice dimensionale direct de la tastatură este cunoscută dinainte cu atribuirea valorilor standard ale valorilor elementelor DIM D (3) INPUT N =, N DATA 23, -13, 9,8, 77, 45 randomiza TIMER D (1) = 12,6 DIM M (N ) DIM M (5) INTRARE "N ="; ND (2) = 5.96 FOR I = 1 TO N FOR I = 1 TO 5 DIM M (N) D (3) = 98 INPUT M (I) SE CITEȘTE M (I) PENTRU I = 1 TO N NEXT I NEXT IM ( I) = INT (RND (1) * 100) NEXT I Pentru a rezuma
11 Sarcini 1. Calculați produsul elementelor matricei. 2. Calculați valorile funcției Y = X * X pentru X = 2,4,6,8. 36 și plasați-le într-o matrice unidimensională Y. 3. Schimbați ordinea valorilor elementelor matrice la contrariul. 4. "Strângeți" matricea numerică, aruncând numere negative din ea. 5. Se specifică o matrice și un număr. Găsiți unde este localizat numărul din matrice. 6. Introduceți primele sute de prime numere. 7. Rotiți matricea pătrată 90, 180, 270 grade în sensul acelor de ceasornic. 8. Aflați dacă există numere identice într-o matrice unidimensională, într-o matrice bidimensională. 9. Numără numărul de numere unice din matrice. 10. Este specificată o serie de numere. Înlocuiți fiecare număr cu suma celor precedente: a) inclusiv cea înlocuită; b) excluderea celei înlocuite.

12 Sarcini 11. Se specifică o matrice unidimensională de 10 elemente. Creșteți numărul pozitiv de 3 ori, reduceți negativ de 2 ori. 12. Se specifică o serie de elemente N. Determinați elementul maxim. 13. Determinați suma elementelor cu un indice de echilibru. 14. Definiti y daca x = x1, x2, x3. x10: y = 2 * x2-4 * x + sin2x 15. Sunt definite două rețele unidimensionale. Imprimați toate elementele matricei obținute prin însumarea și scăderea elementelor din matricele originale cu aceiași indicatori. 16. Completați acest tabel cu elemente ale căror valori sunt egale cu numărul lor de serie dublu. 17. Efectuați un program pentru a înlocui elementele negative ale tabelului cu pătratele lor. 18. Scrieți un program pentru dublarea fiecărui element dintr-o matrice unidimensională. 19. Scrieți un program de recensământ pentru elementele unei matrice unidimensionale în alta. 20. Se dă un tabel întreg. Modificați toate elementele din acest tabel la opusul semnului.
13 Sarcini 21. Găsiți elementul dat într-o matrice unidimensională. Imprimați indexul elementului găsit. 22. Scrieți un program pentru a determina de câte ori numărul 10 apare între elementele unei matrice unidimensionale. 23. Găsiți numărul elementelor din acest tabel, cu atât este mai mare media aritmetică a tuturor elementelor sale. 24. Găsiți cel mai mic element dintr-o matrice unidimensională. 25. Găsiți cel mai mare element dintr-o matrice unidimensională. 26. Găsiți cel mai mic element dintr-o matrice bidimensională. 27. Găsiți cel mai mare element dintr-o matrice bidimensională.
14 1. Calculați produsul elementelor matricei. Dimensiunea INPUT matrice; N DIM S (N) P = 1 FOR i = 1 TO NS (i) = INT (RND (1) * 10) P = P * S (i) NEXT i PRINT array FOR i = 1 TO N PRINT S (i); NEXT I PRINT Produs de elemente; P END
15 2. Calculați valorile funcției Y = X * X pentru X = 2,4,6,8. 36 și puneți-le pe o matrice unidimensională Y. DIM Y (18) x = 2 LA 36 PASUL 2 i = x / 2 Y (i) = X * X NEXT array x PRINT FOR i = 1 TO 18 PRINT Y (i) ; NEXT I END
16 3. Schimbați ordinea valorilor elementelor de matrice în sens invers.
17 4. "Strângeți" matricea numerică, scotând numere negative din ea. INPUT dimensiunea matricei; N DIM A (N) K = 0 PENTRU i = 1 la N PRINT, introduceți; i; elementul matrice INTRARE A (i) IF A (i)
18 5. Se specifică o matrice și un număr. Găsiți unde este localizat numărul din matrice. Numărul INPUT; Dimensiunea C INPUT a matricei; N DIM A (N) matrice PRINT FOR i = 1 TO N A (i) = INT (RND (1) * 100) DACĂ A (i) = C THEN K = I PRINT A (i); NEXT i element de tip PRINT egal cu numărul; C; localizat pe locul; K;
6. Introduceți primele sute de prime numere. DIM A (100)
7. Rotiți matricea pătrată 90, 180, 270 grade în sensul acelor de ceasornic.
8. Aflați dacă există numere identice într-o matrice unidimensională, într-o matrice bidimensională.
22 9. Numărați numărul de numere unice din matrice.
23 10. Este indicată o serie de numere. Înlocuiți fiecare număr cu suma celor precedente: a) inclusiv cea înlocuită; b) excluderea celei înlocuite.
24 14. Definiti y daca x = x1, x2, x3. (10) Y (10) FOR i = 1 la 10 X (i) = INT (RND (1) * 10) Y (i) = 2 * X (i) ^ 2-4 * X (i) + SIN (X (i)) ^ 2 X (i)
25 17. Pentru a crea un program pentru înlocuirea elementelor negative ale tabelului cu pătratele lor. INPUT N, M DIM A (N, M) FOR i = 1 TO N FOR j = 1 TO MA (i, j) = INT (RND (1) * 10) * (- 1) ^ (INT (RND (1 ) * 10) A A (i, j), dacă A (i, j)
18. Scrieți un program pentru dublarea fiecărui element dintr-o matrice unidimensională. INPUT dimensiunea matricei; N matricea DIM A (N) PRINT; matricea dublată FOR i = 1 TO N A (i) = INT (RND (1) * 100) PRINT A (i), A (i) * 2 NEXT i
27 22. Scrieți un program pentru a determina de câte ori apare numărul 10 între elementele unei matrice unidimensionale. INPUT dimensiunea matricei; N DIM A (N) K = 0 PENTRU i = 1 TO N A (i) = INT (RND (1) * 100). NEXT I PRINT numărul elementelor egale cu 10; K END
28. Gaseste cel mai mic element dintr-o matrice unidimensionala. (I) = INT (RND (1) * 10) NEXT i K = 1 MIN = A (1)
29