Matricea transformării coordonatelor
În spațiul E n luăm două baze distincte e 1, e 2. e n și E 1, E 2. E n
Motivarea este efectuată pentru cazul n = 3. Același vector x față de diferitele baze are coordonate diferite. Putem scrie:
Orice vector al celei de-a doua baze poate fi extins în termeni de prima bază, adică
Datorită unicității expansiunii față de această bază, trebuie să echivalăm coeficienții pentru vectorii e 1, e 2, e 3 și obținuți. atunci
Introducem matrice
Apoi, relațiile obținute pot fi scrise în matricea X = Z ⋅ X '.
Matricea Z este numită matricea de transformare a coordonatelor de la baza veche la cea nouă, adică din baza e 1, e 2. e n la baza E 1, E 2. E n. Mai mult decât atât, coloanele matricei de transformare a coordonatelor sunt coordonatele vectorului noii baze E 1, E 2. E n cu privire la baza veche e 1, e 2. e n.
Schimbarea matricei unui operator liniar la trecerea la o nouă bază
Fie operatorul liniar A definit în spațiul E n. y = A ⋅ x
Sau Y = A⋅X. unde X (x 1, x 2 x n) T și Y (y 1, y 2 y n) T sunt matricele de coloane compuse din coordonatele vectorilor x și y în raport cu baza dată n 1, e 2. e n. A este matricea operatorului liniar A.
Alegem în același spațiu În altă bază E 1, E 2. E n. În ceea ce privește noua bază, matricea operatorului liniar A este diferită. Denumim prin T matricea de transformare a coordonatelor și prin X 'și Y' sunt matrice cu o singură coloană, compuse din coordonatele vectorilor x și y față de noua bază, adică
Înlocuim rezultatul obținut în forma generală, obținem: T ∙ Y '= A ∙ T ∙ X'
Înmulțirea părților stângi și drepte ale egalității din stânga cu T -1. obținem: Y '= T -1 ⋅ A ∙ T ∙ X'.
Deci, dacă vom trece la o nouă bază în E n, atunci matricea operatorului liniar se va schimba și în cel mai general caz va fi egală cu T -1 ⋅ A ⋅ T.
Un exemplu. Operatorul A în baza spațiului E 3
Găsiți matricea în bază
Soluție: Matricea operatorului în noua bază se găsește prin formula B = T -1 AT. unde T este matricea de tranziție de la baza veche la cea nouă. Matricea de tranziție se găsește din formula T = X -1 ⋅ Y.
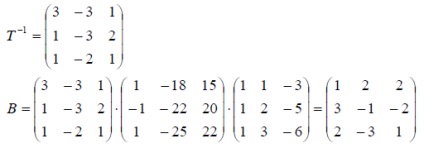
Conjugat și operator de auto-adjunct
Să presupunem că într-un spațiu Euclidian adevărat E n un operator liniar A
Definiția 1. Operator A * în timp real euclidian E n spațiu se numește un conjugat în raport cu operatorul liniar în același spațiu, în cazul în care matricea în orice bază ortonormală a spațiului este nirovannoy transpusă matrice în ceea ce privește operatorul A.
Proprietățile operatorului adjunct
1. E * = E, unde E este operatorul de identitate, adică Operatorul a cărui matrice E este identitatea în E n
4. Dacă A-1 există, atunci (A -1) * = (A *) -1.
Definiția 2. Un operator liniar A definit într-un spațiu euclidian real E n. se numește auto-îmbinare. sau simetrice. Dacă trimite cu operatorul său adjunct A *. și anume dacă A * = A.
Matricea unui operator auto-adjunct coincide cu transpunerea în orice bază ortonormală, adică este simetric în raport cu diagonala principală.
Proprietățile unui operator auto-adjunct
1. dacă A * = A. B * = B. atunci (A + B) * = A * + B * = A + B;
2. Dacă A este un operator non-degenerat auto-adjuint, atunci (A -1) * = (A *) -1 = A -1.
Dovada. Într-adevăr, dacă există A -1 și în plus A * = A. atunci, prin proprietatea 4 a operatorului adjoint, obținem (A -1) * = (A *) -1 = A -1;
3. Dacă A este un operator de auto-îmbinare în spațiul real E n. atunci egalitatea deține:
Vectorii proprii și valorile proprii ale unui operator liniar
Fie A un operator liniar. Fie x∈Ε 1. unde E 1 este un subspațiu al spațiului E n. Vectorul y = A x poate aparține subspațiului E 1. Sau poate să nu aparțină.
Definiția. Subspațiul E 1 este considerat a fi invariant față de co-operatorul A. dacă A x∈ Ε 1. ∀ x∈ Ε 1.
Definiția. Un vector nenulos x este numit vector propriu al operatorului liniar A. Dacă există un număr λ. că egalitatea A x = λ x va fi îndeplinită. În acest caz, numărul λ este numit valoarea proprie (valoarea proprie) a operatorului A. corespunzătoare vectorului x. Setul tuturor valorilor proprii ale operatorului A se numește spectrul acestuia.
Să luăm în considerare valorile proprii și vectorii proprii ai operatorului liniar A. Considerăm cazul pentru n = 3. Astfel, să presupunem că, într-o anumită bază, operatorul A are o matrice
și permite matricea cu o coloană să corespundă vectorului x. Apoi, după definiție
Problema a fost redusă la rezolvarea unui sistem de ecuații lineare omogene scrise sub formă de matrice. Evident, acest sistem are o soluție nonzero dacă det (A - λE) = 0. Ecuația det (A - λE) = 0 se numește ecuația caracteristică a operatorului A; Debitul polinomial (A - λE) se numește operatorul caracteristic polinomial A, respectiv. În forma coordonată, ecuația caracteristică arată astfel:
Rezolvind-o, găsim valorile proprii ale operatorului liniar. Apoi, pentru suma elementelor diagonale ale matricei A. care se numește urmă a acestei matrice trA sau a urmei operatorului A (trA). formula este valabilă. În plus, detA = λ 1 λ 2 λ 3.
După ce se găsesc valorile proprii ale operatorului liniar A, rămâne să le substituim la rândul lor în ecuație și să găsim vectorii proprii corespunzători x (1). x (2). x (3)
Un exemplu. Identificați valorile proprii și valorile proprii ale unui operator liniar al cărui matrice
Soluția. Prin definiția unui vector propriu, putem scrie o matrice-coloană corespunzătoare vectorului x necesar operatorului liniar A;
În forma matricei obținem:
Sistemul este omogen, prin urmare, are un număr infinit de soluții dacă determinantul sistemului este zero, adică avem ecuația caracteristică:
Rezolvând-o, obținem astfel de valori proprii λ 1 = -1; λ 2 = 3.
Gasim vectorii proprii corespunzatori.
1) λ 1 = -1 înlocuim în ecuația pe care o obținem
unde t (1) este un anumit parametru. Astfel, avem un set de vectori coliniari corespunzând primei valori proprii λ 1 = -1:
Acest vector este usor de normalizat, atunci primim un eigenvector unit care corespunde primei valori proprii λ1 = -1 adica,
2) λ 2 = 3 înlocuim în ecuație, obținem
În concluzie, rețineți că mulțimea tuturor vectorilor y = A x. unde x∈ E n. este numit intervalul de valori ale unui operator liniar A în E n. și mulțimea tuturor vectorilor x∈E 1 ⊂ E n. astfel încât A x = 0, se numește kernelul unui operator liniar.
Proprietățile valorilor proprii și vectorilor proprii ai unui operator auto-adjunct
Considerăm că operatorul auto-adjunct A. definit în spațiul Euclidian real E n. Prin definiția matricei sale, A este simetrică.
THEOREM 1. Valorile proprii ale operatorului A autoadezvolt sunt numere reale.
Teorema 2. Vectorii proprii care corespund celor două valori proprii distincte ale unui operator auto-îmbinat sunt ortogonali.
> Dovada. Să fie diferitele valori proprii ale unui operator A-adjunct A și x 1. x 2 sunt valorile proprii corespunzătoare acestora. atunci
Dar asta este. părțile stângi ale egalităților sunt egale, prin urmare, scăzându-le termenul pe termen, primim: aceasta înseamnă că vectorii proprii x 1. x 2 sunt ortogonali.
Notă. Deoarece vectorii proprii ai operatorului A sunt ortogonali, ei pot fi luați ca bază a spațiului liniar în care este definit acest operator liniar. După împărțirea fiecărui vector cu lungimea sa, obținem o bază ortonormală.
Teorema 3. În baza vectorilor proprii ai unui operator auto-adjunct, matricea acestui operator este diagonală, iar elementele diagonale sunt propriile sale valori.
Dovada. Dovada este de pentru n = 3. Fie e 1. e 2. e 3 - vectori ai unei unități autoadjunct Operatorul cu privire la o bază a spațiului E liniar 3. corespunde autovalorile operatorului liniar, adică . Luăm vectorii e 1. e 2. e 3 ca bază a unui spațiu liniar. Este evident că pe această bază vectorii au coordonate:
. În consecință, matricea A a operatorului A în baza e 1. e 2. e 3 are forma:
Alegerea unei astfel de baze, în care matricea unui operator liniar are o formă diagonală, se numește reducerea matricei în forma diagonală.