Construcția zonelor inele
O gaură într-un ecran opac care se întinde de la distanță. Această gaură va trece numai o parte din valul sferic care emană din. Să determinăm acțiunea acestui val într-un punct situat pe o linie dreaptă
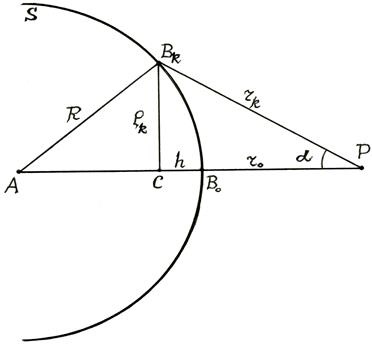
Pentru calcularea dimensiunilor zonelor inele ale minei, care trece prin centrul gaurii, la o distanta de la varf. Pentru aceasta vom împărți valul -
Suprafața zonelor inelare este zona Fresnel, construită astfel încât distanțele de la marginile zonelor învecinate până la punct diferă la jumătate din lungimea de undă:
Apoi oscilațiile care ajung până la un punct din părțile corespunzătoare din zonele învecinate vor avea o diferență de drum. adică vor ajunge într-un punct în faze opuse.
Amplitudinea oscilațiilor care provin din zonele individuale depinde de aria acestei zone, distanța de la zona la și unghiul de înclinare dintre suprafața și normala la suprafață. Mai întâi de toate, să arătăm că zonele din zone sunt aproximativ egale. Indicați cu - zona de rază -. Din fig. 4 avem
Dar în conformitate cu (1), distanța zonei a-a este mai mare decât distanța:
din (4), presupunând că lungimea de undă este mult mai mică decât distanța, obținem aproximativ
după care egalitatea (3) ia forma
Suprafața unui segment sferic de rază este
, înlocuind aici (6), obținem
În acest segment scade - zonele inelare din care zona unei zone poate fi reprezentată ca diferență în zona acestui segment și segmentul care acoperă zona:
Astfel, aria zonei în această aproximare nu depinde de numărul său, adică zonele tuturor zonelor sunt aproximativ egale. În consecință, amplitudinile oscilațiilor care provin de la zone individuale până la punct depind doar de distanța și unghiul pe care direcția îl face cu normalul față de suprafața zonei. Pe măsură ce numărul zonei crește, distanța crește și unghiul de înclinare crește, astfel încât amplitudinea oscilațiilor crește. ajungând până la punctul din zonele individuale. ar trebui să scadă monoton cu numărul zonelor în creștere:
Deoarece fazele oscilațiilor care ajung la un punct din două zone învecinate sunt opuse, amplitudinea oscilației totale. cauzate de acțiunea zonelor este
unde semnul ultimului termen este pozitiv pentru ciudat și negativ pentru even.
Evident, pentru un număr par de zone, acțiunile lor se slăbesc reciproc în perechi, iar amplitudinea oscilației totale în acest punct este nesemnificativă; Pentru un număr impar de zone, acțiunea uneia dintre zone rămâne neafectată, iar amplitudinea este mai mare decât pentru un număr par de zone. Obținem o valoare mai precisă împărțind toți termenii ciudați în doi termeni în suma (9):
Apoi pentru ciudat, obținem
și chiar dacă avem
Deoarece, în conformitate cu cele de mai sus, amplitudinea scade monoton cu număr tot mai mare, atunci putem pune aproximativ de amplitudine cauzata de unele - orice - lea suprafață egală cu jumătate din suma amplitudinile oscilațiilor cauzate de - primul și - a doua zonă:
, prin urmare, toți termenii din seria (10) și (11), separați prin paranteze, sunt egali cu zero și, prin urmare, sunt impar:
Dacă numărul de zone este suficient de mare, atunci amplitudinile oscilațiilor cauzate de zonele învecinate și zonele diferă foarte puțin una de alta, de la care aproximativ
Astfel, egalitățile (12) și (13) iau forma:
unde semnul "" și semnul "-" corespund unui număr par de zone.
Prin formula (2), raza celei de-a doua benzi este dată de
Presupunem, atunci ne neglijăm
, înlocuind aici cu valoarea lui (6), obținem
, în cele din urmă, înlocuind, prin (5), găsim
Rețineți că în același timp există o rază a găurii în cauză pe ecran. Din aceasta rezultă că deschiderea razei deschide o parte din frontul de undă pe care se află numărul de zone
Pentru partea frontală a incidentului de pe ecran, formula (17) ia forma:
unde este unghiul la care este văzut gaura din ecran, din fig. 4.
Amplitudinea oscilației totale într-un punct depinde de numărul de zone deschise. Pentru dat: - lungimea de undă, - raza găurii din ea și localizarea ecranului - numărul de zone deschise va fi diferit.
În acele puncte pentru care este ciudat, amplitudinea oscilației totale este mai mare și la acele puncte pentru care este uniform, este mai mică. Pătratul amplitudinii va determina energia oscilațiilor. La rândul său, energia oscilațiilor luminoase determină iluminarea. Astfel, atunci când se deplasează de-a lungul unei linii drepte, Fig. 3, ne vom întâlni apoi mai mari, apoi iluminări mai mici.
Când aceleași date, și așa mai departe. E. La o anumită locație a sursei de lumină, un ecran cu o deschidere și punctul de observație va depinde de dimensiunea găurii și relația sa cu lungimea de undă (18), (19).
Astfel, am ajuns la concluzia că nici o lumină rectiliniu propagates, iluminare la punctul determinată de mărimea și poziția găurilor este determinată de acțiunea tuturor punctelor situate pe partea deschisă a Wavefront.
Dacă dimensiunile deschiderii sunt mărită până la infinit, adică rămân deschise sau nu acoperă întreaga suprafață a frontului undei