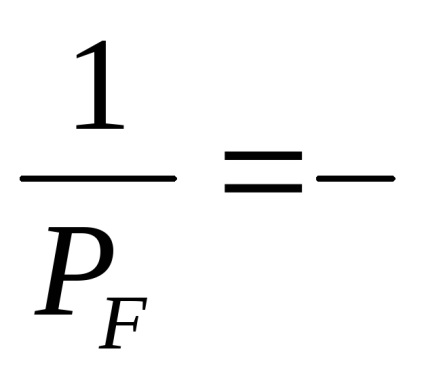Atunci când triangularea este egalizată în ecuațiile de corecție pentru direcții, în plus față de corecțiile la valorile aproximative ale coordonatelor, se fac corecții la unghiurile de orientare ale stațiilor

unde C și A sunt matricele de coeficienți pentru vectorii de corecție din unghiurile de orientare


Acesta va corespunde unui sistem de ecuații normale
unde este matricea de greutate a direcțiilor măsurate.
Aplicarea metodei de substituție și eliminarea

Acest sistem transformat poate fi obținut într-un alt mod.
Lăsați următoarele ecuații de corecții să corespundă direcțiilor măsurate la stația i
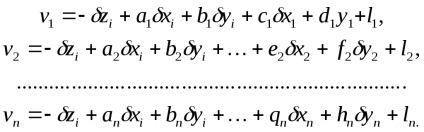
Următorul sistem de ecuații normale îi va corespunde:
Dacă scădem din prima ecuație a sistemului (134)
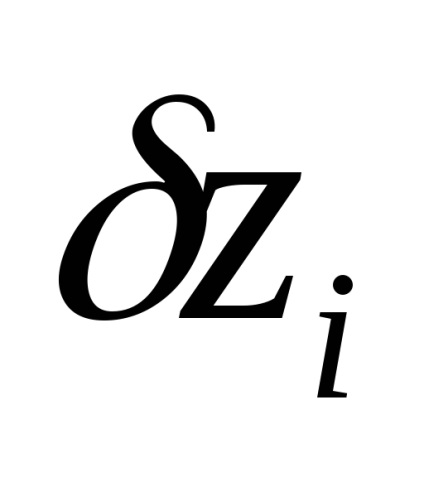
și înlocuim-o în rest, obținem un sistem echivalent
Continuând de aici, este ușor de observat că matricea ecuațiilor normale poate fi compilată pe baza ecuațiilor corective existente, cu adăugarea la fiecare stație a așa-numitei ecuații totale
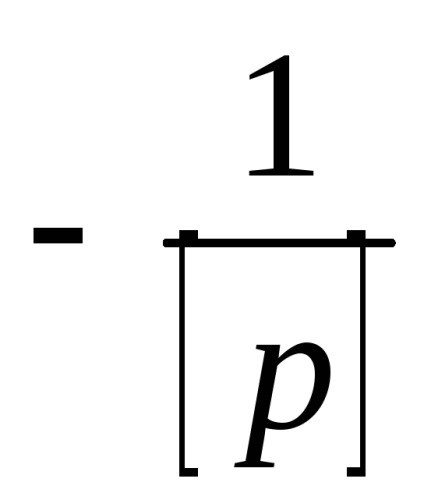
Un exemplu de ajustare a unei rețele geodezice prin metoda parametrică
Pentru a egala rețeaua geodezică prezentată în Fig. 21 în exemplul de egalizare prin metoda corelativă.
Coordonatele aproximative ale punctelor D și E sunt după cum urmează
Rețineți că acestea pot fi găsite prin măsurători într-o rețea geodezică.
În primul rând, pentru a calcula termenii liberi ai ecuațiilor de corecție, este necesar din valorile coordonatelor aproximative ale punctelor determinate și din coordonatele celor inițiale să se calculeze unghiurile de direcție și lungimile laturilor cu o precizie corespunzătoare coordonatelor aproximative presupuse. Pentru aceasta, problemele geodezice inverse sunt rezolvate prin formule
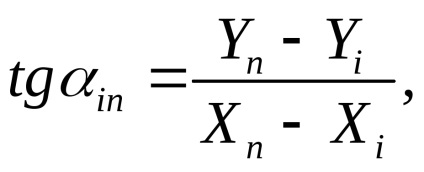
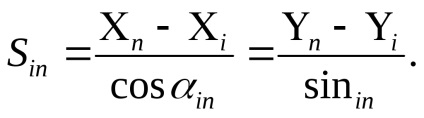
unde i, n sunt numerele elementelor.
După calcularea exactă a lungimilor laturilor și a unghiurilor de direcție de la coordonatele preliminare, se calculează termenii liberi ai ecuațiilor de corecție (Tabelul 15). În același tabel, coeficienții
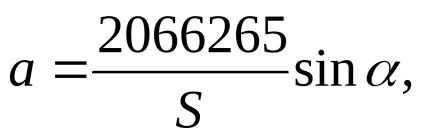
necesare pentru compilarea unei matrice de coeficienți ai ecuațiilor de corecții.
În conformitate cu (115) și (137), ecuațiile de corecție pentru fiecare direcție măsurată vor avea forma
iar pentru partea măsurată forma (108).
Sistemul de ecuații de corecție pentru întreaga rețea este prezentat în Tabelul 16.
În același loc, pentru fiecare stație se elaborează și ecuațiile totale ale formulei (136).
Sistemul ecuațiilor normale
este prezentat în Tabelul 17.
Sistemul ecuațiilor normale
Tabelul 17 arată numai triunghiul superior al matricei ecuațiilor normale
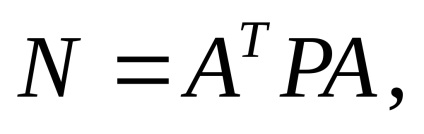
vector al termenilor liberi
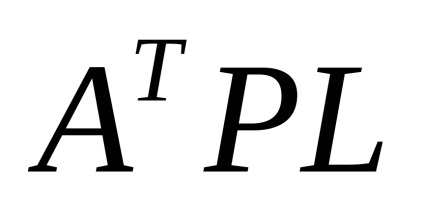
Sistemul de ecuații normale este compilat aici în același mod ca și sistemul de ecuații normale corelate. Dar, în acest caz, coloanele corespunzătoare se înmulțesc cu greutățile de măsurare, și nu cu reciprocalele lor, ca în metoda corelativă.
Soluția ecuațiilor normale conform schemei gaussiene este dată în Tabelul 18.
Conform corecțiilor primite la coordonatele punctelor determinate D și E și coordonatele lor aproximative, valorile finale

Pe baza (135), se calculează corecția pentru unghiul de orientare pentru fiecare stație.
Soluția ecuațiilor normale conform schemei Gauss
Luând în considerare această corecție și valorile corecțiilor la coordonatele aproximative ale punctelor determinate, pe baza ecuației pentru corecțiile direcțiilor (138), se calculează corecțiile direcțiilor. Corecțiile la laturile măsurate sunt calculate prin simpla înlocuire a corecțiilor de coordonate în ecuațiile corecțiilor laterale (108). Calculele acestora sunt prezentate în Tabelul 16.
Corecțiile obținute cu precizia calculelor trebuie să coincidă cu corecțiile constatate prin metoda corelativă de egalizare.
Calculul erorii pătrunderii medii a unei unități de greutate este de asemenea realizat prin formula (94). În cazul general, în metoda parametrică, numărul măsurătorilor în exces este determinat de formula
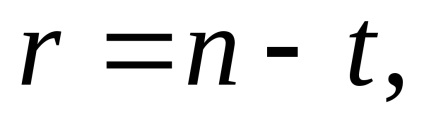
unde n este numărul de ecuații de corecție, t este numărul de parametri necunoscuți. Când direcțiile sunt egale, numărul t este calculat de formula
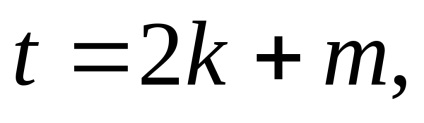
unde k este numărul de puncte care vor fi determinate, m este numărul de stații din care au fost măsurate direcțiile. Dacă la fiecare punct al direcției au fost măsurate o singură dată, atunci numărul m este egal cu numărul tuturor punctelor, inclusiv cele inițiale. Acest număr este egal cu numărul tuturor unghiurilor de orientare, adică numărul de grinzi de direcție măsurate.
Valoarea erorii pătrate medii a unei unități de greutate este o estimare a standardului din (128). În plus, prin formula (128), putem calcula estimarea preciziei oricărei funcții după ajustare. În metoda parametrică este convenabil să se estimeze acuratețea punctelor determinate prin formula (131). În acest caz, este necesar să se inverseze matricea ecuațiilor normale N.
Tratamentul său poate fi efectuat în diverse moduri. Metoda cea mai convenabilă este excepția modificată a Iordaniei.
Esența lui este după cum urmează:
1) În matricea inițială, elementul de rezolvare
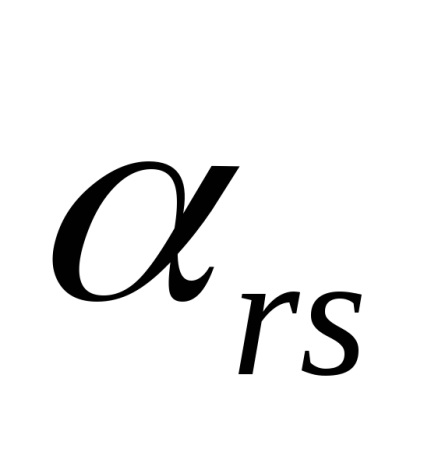
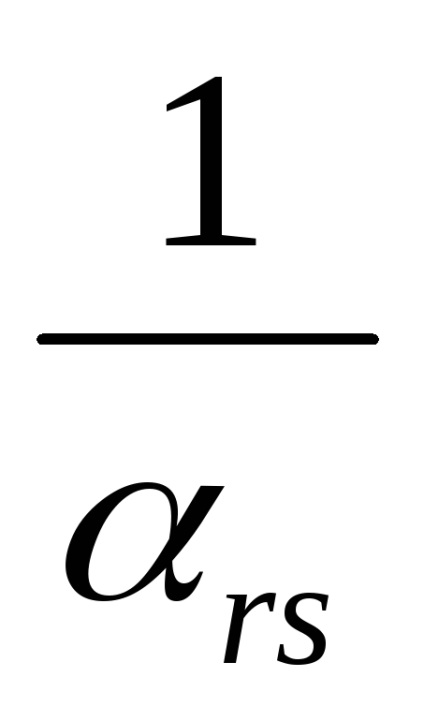
2) Elementele rămase ale șirului de rezolvare r sunt împărțite într-un element de rezolvare.
3) Elementele rămase ale coloanei de rezoluție S sunt împărțite într-un element de rezolvare și sunt inversate.
4) alte elemente sunt calculate prin formula:
Se recomandă efectuarea calculelor cu păstrarea a două cifre semnificative după punctul zecimal.
La prima etapă a excepției Jordan, elementul diagonal 4.17 este adoptat ca rezolvator.
Rezultatul este o matrice
În a doua etapă, al doilea element transformat al matricei (141) va fi rezolvat, i. E. 7.90.
La a treia etapă, elementul diagonal al matricei 9142) este folosit ca resolver. 9.75.
În a patra etapă, adică ultimul element de rezolvare va fi 8,13.
Rezultatul final este prezentat sub forma unei matrice
care va fi inversul matricei (139).
Controlul corectitudinii inversiunii este egalitatea matricei de identitate a produsului matricelor (139) și (144) cu o precizie de 0,1. În plus, atunci când se schimbă de la o etapă a excepțiilor de la Iordan la cealaltă, este necesar să se monitorizeze simetria matricelor care se formează. Numai în șirul de rezolvare spre stânga și în coloana de rezolvare de sus, din elementul de rezolvare, matricele diferă doar prin semne.
În cele din urmă, conform formulei (131), găsim
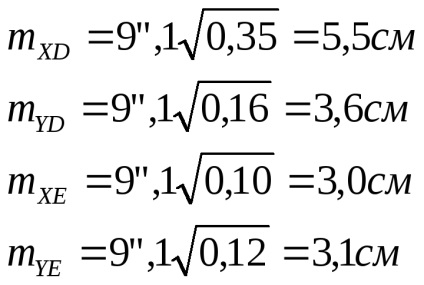
Erori în poziția generală a punctelor D și E vor fi
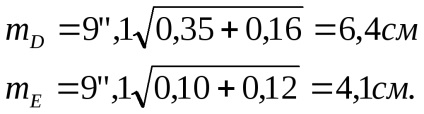
Folosind matricea (144) și coloana A T PL din Tabelul 17, prin formula (130), se pot găsi corecții la coordonatele aproximative ale punctelor determinate. ele vor fi egale cu cele calculate în Tabelul 18 pentru rezolvarea ecuațiilor gaussiene normale.
Estimarea preciziei unei funcții individuale poate fi de asemenea realizată utilizând formula Gauss. În acest caz, o funcție de greutate este calculată din parametrii determinați
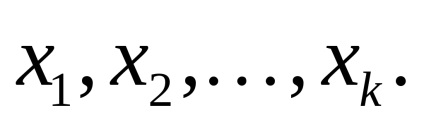
unde
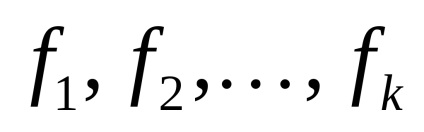
În această problemă, acești parametri sunt corecții la coordonatele aproximative ale punctelor determinate, adică,
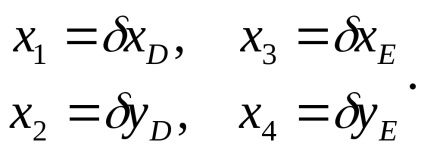
Greutatea inversă a acestei funcții este egală cu