În Fig. 337 prezintă o întoarcere a suprafeței elicoidale. formată de mișcarea segmentului AB. Linia dreaptă definită de acest segment intersectează axa cu același unghi în toate pozițiile (în figura 337 unghiul este de 60 °). Deplasarea capetelor segmentului de-a lungul axei este proporțională cu deplasarea unghiulară a segmentului.
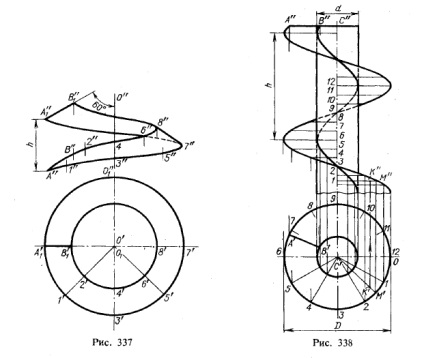
Punctele A și B formează o linie elicoidală cilindrică, ca și toate punctele segmentului AB, și, prin urmare, pentru a imaginii cu mai multă precizie eseu elicoidal mp Suprafata. π2 ar trebui să-și petreacă, eventual, mai multe proeminențe helix descrise diferitele puncte ale segmentului AB, și apoi să efectueze curbele, plicuri ale acestor proiecții. În practică, în loc de această construcție greoaie, se trasează de obicei linii drepte, simultan cu proiecțiile liniilor elicoidale (vezi Figura 345). Dacă panta generatoarei în raport cu axa cilindrului nu este egală cu 90 ° (de exemplu, 60 ° în Fig. 337), suprafața elicoidală este numită oblic. Dacă acest unghi este de 90 °, se formează o suprafață elicoidală dreaptă. Este arătat în Fig. 338.
Suprafața prezentată în Fig. 338, este un conoid. Într-adevăr, generatorul este o linie dreaptă; este paralel în toate pozițiile la un anumit plan (în acest caz perpendicular pe axa cilindrului): generatorul intersectează două linii de ghidare, o curbă și o linie dreaptă (axa cilindrului). Deoarece ghidajul curbei este o linie de șurub, atunci un astfel de conoid se numește șurub. Un alt nume este elicoidul direct 1).
În Fig. 338 conoidul elicoidal este prezentat împreună cu un cilindru circular având o axă comună cu el; Ca rezultat, pe suprafața cilindrului se formează o linie elicoidală cilindrică, a cărei înălțime este aceeași cu pasul ghidajului de helix. Suprafața cuprinsă între cele două linii de șurub este numită conoid elicoidal inelar.
Cel prezentat în Fig. 337, suprafața, numită spirala elicoidală elicoidală, este numită și helikoidul oblic. Caracteristic pentru o astfel de suprafață este aceea că generatorul rectilinie traversează în toate ghidurile sale poziții - o linie cilindric elicoidal și o linie dreaptă (suprafață axa), în care generatoarea intersectează axa la un unghi constant nu este egal cu 90 °. În toate pozițiile generatorul este paralel cu generatoarele unui anumit con de revoluție. axa coincide cu axa liniei elicoidale (figura 339, stânga). Dacă, de exemplu, este necesar să primească proiecția frontală formând o helicoid oblic care trece prin punctul C, este necesar să se înceapă cu o proiecție orizontală a generatoarei, adică. E. Raza hold S'C“, un punct punct de căutare C c'1„1, și un front proiecție formând SC1. con și apoi transporta C „D“, în paralel cu S „C“ 1.
În Fig. 339 din dreapta arată suprafața elicoidală formată de mișcarea unui segment tangențial la suprafața cilindrului. Construcția reduce din nou la găsirea proiecțiilor
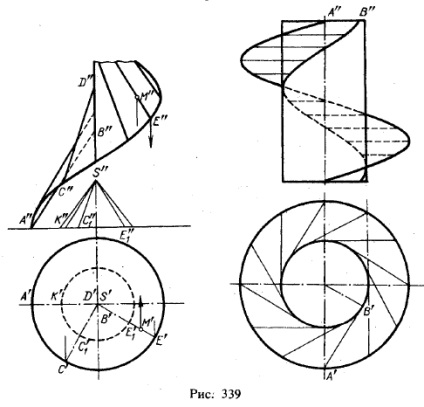
șuruburi formate din două puncte: capătul A al segmentului și punctul de contact B. Segmentul poate fi direcționat în raport cu axa, fie într-un unghi drept (așa cum este prezentat în figura 339), fie sub un unghi ascuțit.
1) Helicoidal (Fr.) - elicoidal; helice (fr.) - o spirală, o spirală. Ei spun, de asemenea, heliwoid. Un helixoid este înțeles ca o suprafață cu șurubelui.
Încrederea prezentată în Fig. 339 din dreapta este un cilindru (vezi pagina 143). Într-adevăr, formând în toate pozițiile rămâne paralelă cu un plan și diapozitive pe două șine - curbe spațiale; planul paralelismului este perpendicular pe axa cilindrului; formând tangenta la suprafața cilindrului (puncte ating forma o linie elicoidală cilindrică) și în același timp, traversează linia șurub de ghidare, a cărei axă coincide, axa cilindrului. Suprafața prezentată în Fig. 339 în dreapta, se numește un cilinderoidoid elicoidal. La formarea o astfel de suprafață este traversat cu axa cilindrului, face cu această axă un unghi nu este egal cu 90 °, atunci suprafața nu mai este aparține categoriei cilindroid, se numește un inel helicoid oblic.
Suprafețele cu șurub considerate sunt clasificate ca neconvertibile. Dar există o suprafață elicoidală, care este considerată a fi implementabilă. Aceasta este o suprafață cu o nervură de întoarcere, care este o spirală cilindrică (vezi figura 317). O astfel de suprafață elicoidală se numește un elicoid care se deschide.
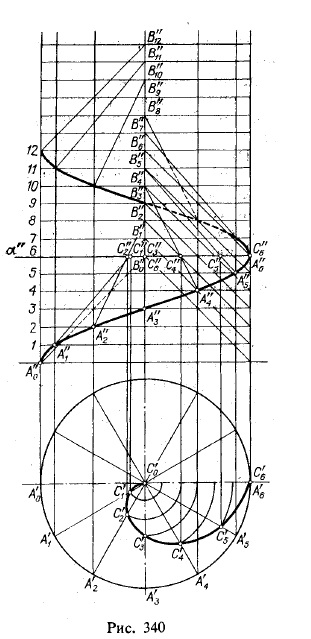
În Fig. 340 suprafața elicoidului oblic este prezentată la intersecția cu pătratul. α, perpendicular pe axa acestei suprafețe; curba de intersecție este prezentată în Fig. π1. fără distorsiuni, deoarece α || π1. Această curbă este spirala lui Archimedes 1).
Construcția acestei curbe se reduce la următoarele. Divizarea a'0 S'0 S'6 Unghi (180 °), în mai multe (în acest caz șase) de părți egale, pe aceeași între ei părți egale ale S'0 segmentului divizat și S'6. La o rază de la un punct de A'1 S'0 S'0 amâne, la o rază S'0 A'2 amâna S'0 c2 = 2C'0 c'1 și t. D.
Acum, să ne acordăm atenție modului în care sunt construite proiecțiile punctelor care aparțin suprafețelor șuruburilor drepte și oblice.
Pentru o suprafață elicoidală dreaptă, aceasta este prezentată în Fig. 338. Să presupunem că punctul K aparținând suprafeței este dat de proiecția orizontală a lui K '. Pentru a găsi proiecția K“, este necesar să se elaboreze o proiecție orizontală a modelelor în care punctul trebuie să fie K t. E. Se efectuează o CM rază«prin K proiecție». În conformitate cu punctul M„vom găsi punctul M“și dețin o vedere frontală a generatorului, în paralel A "B". Pe această linie dreaptă găsim proiecția R "2).
În cazul în care este dat proiecția „și necesitatea de a găsi K“, prima prin K“țineți linia perpendiculară pe axa șurub până la intersecția cu proiecția elicei la punctul M„la acest punct, vom găsi punctul M «și S'M rază» - punctul K '.
Precizia legată de AICI acuratețea undă sinusoidală (Helix proiecție frontală), deoarece punctul M „este pe ea.
1) Suntem interesați de dovezi pentru edițiile anterioare.
2) Acordați atenție vizibilității punctului K în raport cu pătratul. π2. la "opacitatea" punctului de suprafață elicoidală K este invizibilă.
În cazul suprafeței oblice elicoidal (Fig. 339, stânga), în cazul în care proiecția daya lui M „și M trebuie să găsească„trage prin punctul M“raza E'S« la punctele E»și E'1 găsi punctul E„și E“1. holding de proiecție S „E“ a conului 1 și paralel la acesta prin punctul E „proiecție formând o suprafață elicoidală. Pe această proiecție obținem proiecția M ".
Dacă proiecția este definită de M „și trebuie să găsească M“, este necesar să se construiască o curbă (spirala lui Arhimede) de la intersecția planului oblică a unei suprafețe elicoidale, a avut loc la nivelul punctului M“perpendicular pe axa suprafeței, și pe spirala pentru a găsi punctul M '.
Suprafețele șuruburilor prezentate în Fig. 337 - 340, nu se poate desfășura exact într-un avion. Pentru suprafața elicoidală dreaptă prezentată în Fig. 338, putem deplasa aproximativ fiecare revoluție individuală așa cum se arată în Fig. 341. O maturare a unei revoluții poate fi reprezentată (aproximativ) ca parte a unui inel plat.
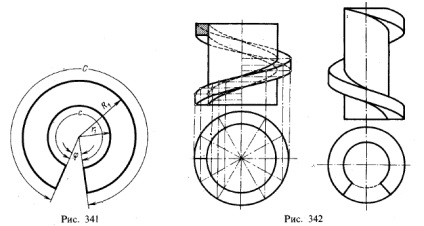
Pentru a construi o astfel de parte a inelului, este necesar să găsim razele R1 și r1 și unghiul φ. Dacă terenul suprafeței șurubului (. 338 Fig) este notată cu h, iar diametrele (diametrul cilindrului) exterior și interior - prin D și d, formula prezentată la p. 133, lungimile secțiunilor liniilor elicoidale sunt exprimate după cum urmează:
Deoarece liniile elicoidale sunt desfășurate în acest caz în arce concentrice cu același unghi central, atunci c: C = r1: Ri și, în consecință,
Indicăm lățimea suprafeței elicoidale, adică diferența. prin a, obținem R1 = r1 + a, din care rezultă că unghiul φ poate fi determinat din formula
Set D = 100 mm, d = 60 mm, h = 50 mm. Gasim a = 20 mm, Σ≈318 mm, ≈195 mm, r1 ≈32 mm, R1 ≈52 mm, φ≈10 °.
Egal raze R1 = 52 mm, d1 = 32 mm în două cercuri concentrice, construi unghiul central de φ = 10 ° și, astfel, să aloce o parte a inelului, care este o grupare (aproximativ) scanare o rotire a unei suprafețe elicoidale.
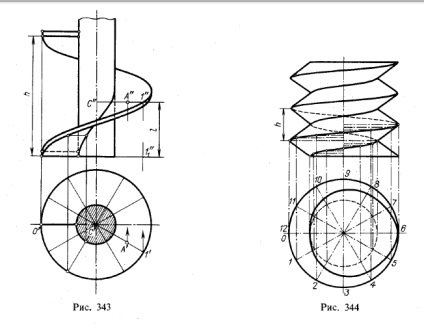
Cu câteva astfel de rotații, fiecare rotire poate fi combinată cu o tijă cilindrică cu diametrul d (după cum se arată în figura 343) și se fixează unul după altul la rotațiile pivotate pe tija.
La fel ca și cu punctul de mișcare elicoidală este format dintr-o linie elicoidală și mișcarea elicoidală a segmentului se obține o suprafață elicoidală, poate primi un corp cu șurub, dacă forța orice formă plană (de exemplu, pătrat, triunghi, trapez) se deplasează de-a lungul suprafeței cilindrului, astfel încât nodurile Această cifră a fost deplasată de-a lungul liniilor elicoidale, iar planul figurinei a trecut constant prin axa cilindrului. Se formează o proeminență cu șurub, limitată de suprafețe șurub și cilindrice. Construcția unor astfel de proiecții șurub de proiecție se reduce la construcția atât de multe linii în spirală ca noduri în forma selectată.
În Fig. 342 din stânga arată construcția proeminenței șurubului formată de mișcarea patratului. Pătratul continuu se alătură uneia dintre laturile sale către generatorul cilindrului; vârfurile pătratului se mișcă de-a lungul liniilor elicoidale.
Când filetarea unei șuruburi (rotire) este formată prin îndepărtarea unei părți a materialului cu scula de tăiere.
Proeminența șurubului rezultată este limitată de două suprafețe drepte cu șuruburi și două suprafețe cilindrice, exterioare și interioare, care sunt în contact cu suprafața cilindrului propriu-zis. Combinația dintre cilindru și proeminența șurubului se numește șurub. În cazul prezentat în Fig. 342 din stânga, este dat un șurub cu un fir drept. ridicarea proeminenței șurubului pe partea frontală (vizibilă) a cilindrului merge de la stânga la dreapta. Dacă ridicarea proeminenței șurubului de pe fața laterală (vizibilă) a cilindrului a fost lăsat (Fig. 342, partea dreapta), apoi șurubul ar fi stângaci (a se vedea. P. 133, dreapta si helices stanga).
În Fig. 343 prezintă o proeminență cu șurub formată de mișcarea unui dreptunghi adiacent generatorului de cilindri prin partea sa mai mică. Șuruburi de acest tip sunt utilizate în transportoare cu șurub 1).
Același desen ilustrează structura proiecției A „punctul A situat pe suprafața șurubului și o anumită proiecție A“. Construcția similară a indicat în Fig. 338, dar se arată cum se poate evita o eroare în exploatație sinusoidă. Aceasta poate determina intervalul l, determină deplasarea punctului 1 de-a lungul axului filetat când se rotește generatorul din poziția inițială la C1 (adică un unghi O'S'1 „). este necesar să se ia o proporție de x. h = ∠O'S'1“. 360 °, în cazul în care pentru a determina x, și că ne va da valoarea l. Mai departe, este clar din desen.
Șuruburile prezentate în Fig. 342, au un fir pătrat. Dacă în locul unui pătrat luăm un triunghi și îl deplasăm de-a lungul cilindrului în același fel în care a fost făcut cu un pătrat, obținem un șurub cu un fir triunghiular (figura 344). Triunghiul producătoare este adiacent unei părți a cilindrului principal; vârfurile triunghiului formează linii elicoidale, pentru care sunt luate două cercuri. Aceste cercuri sunt împărțite în 12 părți; Punctele de divizare sunt proiectate pe linii orizontale trase prin 12 diviziuni ale pasului șurubului. Suprafața șurubului cu filet triunghiular este o combinație a două suprafețe oblice cu șuruburi. Contur vizibil pe pătrat. π2 se obține prin efectuarea de tangente la proeminențele liniilor elicoidale mari și mici (figura 345). Acesta este de obicei cazul, deși în realitate conturul proiecției suprafeței elicoidale oblice pe pl. π2 este o linie curbată.
În Fig. 346 prezintă construcția secțiunii transversale a unui șurub cu un plan triunghiular de filetă α. Se realizează un plan auxiliar orizontal β care trece prin axa șurubului. În intersecția cu ștuțul pl. β separă triunghiul generator 2), proiecția orizontală a acestuia fiind localizată pe treapta orizontală a pătratului. π; proiecția frontală a laturii AB a acestui triunghi se intersectează cu trasa α "la punctul K", care este proiecția frontală a unuia dintre punctele care aparțin liniei de intersecție a suprafeței elicoidale a pl. α. Pe segmentul A'B obținem o proiecție orizontală a punctului K, care aparține proiecției orizontale a liniei de intersecție dorită a suprafeței elicoidale a pl. α.
1) Un transportor cu șurub (sertar), în caz contrar un transportor cu șurub, este utilizat pentru a deplasa cereale, bucăți mici etc.
2) Planul β separă triunghiul generator în cele două poziții; pe părțile frontale (vizibile) și din spate (invizibile) ale șurubului. În Fig. 346 prezintă construcția pentru fața (vizibilă) a șurubului.
6 V. O. Gordon, M. A. Sementsov-Ogievski
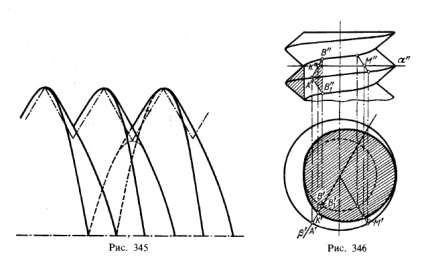
Mai mult, a construit un alt punct M (M „M“) din această secțiune, de data aceasta se reliefează orizontal în plan nu este realizată pentru a arăta că este suficient pentru a identifica doar poziția proiecția orizontală a triunghiului de generare, având una dintre razele De asemenea, în loc frontală completă. proiecție conductoare a triunghiului este suficientă pentru a restricționa proiecția unei fețe așa cum este prezentat în Fig. 346.
Desenând o serie de raze și construind pozițiile corespunzătoare ale triunghiului generator, obținem o serie de puncte pentru proiecția orizontală a conturului secțiunii. Katya poate vedea că secțiunea transversală este limitată de o curbă cu o linie de simetrie; prin urmare, în construcție este posibil să ne limităm la găsirea doar a unei jumătăți din curba liniei,
și să construiască o altă parte din ea ca ramură simetrică. Fiecare jumătate din această curbă a liniei este o spirală a lui Archimedes, a cărei construcție este menționată la p. 159.
În șurubul prezentat în Fig. 344, care produce un triunghi după fiecare rotire în jurul axei cilindrului principal, se ridică într-o poziție adiacentă de mărimea treptei spiralei. Șurubul este obținut din mișcarea unui profil. Un astfel de șurub este numit o singură trecere 1).
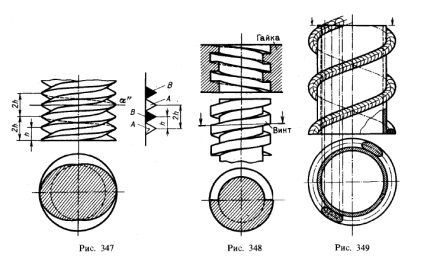
Dacă luăm cele două profiluri și considerându-le conectate între ele, a făcut să se miște de-a lungul liniilor elicoidale, astfel încât fiecare profil, după o cifră de afaceri a crescut la o înălțime de 2h (fig. 347), veți obține un șurub cu două sensuri 2).
În Fig. 348 prezintă un șurub cu filet pătrat drept și o piuliță. Pe o secțiune orizontală se observă segmente de linii drepte, care, împreună cu semicercurile, limitează secțiunea transversală. Aceste segmente corespund faptului că proiecția elicoidală nu este limitată de o suprafață elicoidală oblică, ci de o dreaptă elicoidală.
În Fig. 349 prezintă un șurub bidirecțional al unui transportor cu două șuruburi 3) format prin înfășurarea unui fir de oțel rotund pe o conductă de oțel; Sârmă este fixată la țeavă, de obicei, prin sudare.
Realizarea unui număr de sfere având un diametru egal cu diametrul firului și ale căror centre sunt situate pe o elice (axele bobinelor), conturul prezintă proiecția bobina ca o linie, un cerc plic - proiecția sferelor.
Pe o proiecție orizontală, sunt prezentate secțiunile transversale ale două rotații (conturul proiecției secțiunii este construit ca o linie care înfășoară cercurile obținute prin intersectarea sferelor de mai sus cu un plan).
Întrebări la § 52
- Cum se formează suprafețele șuruburilor drepte și oblice?
- De ce este o suprafață elicoidală dreaptă numită și conoid elicoidal?
- Ce este un conoid elicoidal circular?
- Cum se formează șurubul cilindru?
1) Șuruburile cu o singură direcție sunt denumite uneori șuruburi cu un singur filet, cu un singur filet.
2) Alte nume: șurub cu două filete, cu două filete, cu două filete.
3) Transportorul cu două șuruburi este utilizat pentru mutarea bunurilor bucăți, de exemplu pungi, baloturi etc.