Un lanț de inductanță conectat inductiv, capacitate și rezistență activă poate fi considerat un sistem oscilant, deoarece poate produce oscilații electromagnetice cu frecvență naturală
Aceste oscilații sunt amortizate, deoarece energia concentrată în circuit în momentul oscilației este eliberată ca căldură la rezistența activă în timpul procesului de oscilație.
Apoi, atunci când un emf variabil este inclus în circuitul sursă, acesta poate fi privit ca un element care inițiază oscilații forțate cu o frecvență în circuit. În consecință, ecuația
este ecuația oscilațiilor electromagnetice forțate sub acțiunea unui CEM care se modifică periodic extern.
Folosind cantitățile fizice: frecvența naturală și coeficientul de amortizare, această ecuație poate fi reprezentată în formă.
După cum este bine cunoscut, fenomenul de rezonanță este caracteristic oscilațiilor forțate, care constă în creșterea amplitudinii oscilațiilor forțate, pe măsură ce frecvența acțiunii externe se apropie de frecvența rezonantă, care depinde de parametrii sistemului oscilator.
În circuitul considerat - circuitul oscilator - oscilațiile forțate realizează puterea curentului, sarcina și tensiunea pe condensator, precum și tensiunea pe inductor.
Curbele de rezonanță sunt dependențele valorilor amplitudinii care efectuează oscilații forțate ale cantităților fizice asupra frecvenței acțiunii externe, adică, în cazul nostru, asupra frecvenței sursei emf.
Legea lui Ohm pentru circuitul considerat - circuitul oscilator - permite analiza dependenței amplitudinii intensității curente de frecvența sursei emf :.
Dacă valoarea amplitudinii EMF, precum și valorile rezistenței active, capacității și inductanței sunt constante, atunci valoarea amplitudinii puterii actuale depinde doar de frecvență.
Amplitudinea maximă a curentului: la. În acest caz, frecvența sursei emf coincide cu frecvența naturală a circuitului oscilator :,
adică, pentru oscilațiile forțate ale forței curente, se observă rezonanță.
Figura 155 prezintă curbele de rezonanță pentru amplitudinea curentului ca funcție de frecvența sursei cu rezistență activă diferită a circuitului oscilator. Rezonanța este exprimată mai intens, cu cât rezistența activă este mai mică, adică cu cât este mai mic coeficientul de amortizare.
Oscilațiile de sarcină și tensiune de pe condensator coincid în fază. Să găsim dependența amplitudinii oscilațiilor de sarcină de frecvență. Așa cum se arată în Secțiunea 51. Dacă folosim expresii pentru frecvența naturală și coeficientul de atenuare, această expresie este convertită în forma:
. Valoarea maximă a amplitudinii de sarcină este atinsă cu valoarea minimă a expresiei radicand. Luăm derivatul radicandului în termeni de frecvență și îl echivăm la zero: sau. Înlocuind această valoare în expresia pentru valoarea amplitudinii încărcării, obținem :.
Deci, cum. atunci amplitudinea maximă a tensiunii pe condensator este atinsă la aceeași valoare a frecvenței sursei emf :.
Fig.156 și Fig.157 prezintă curbele de rezonanță pentru valorile amplitudinii încărcării și tensiunii pe condensator pentru diferite rezistențe ale buclei active.
Frecvența de rezonanță pentru încărcare și tensiune este întotdeauna mai mică decât frecvența de rezonanță pentru curent, iar rezonanța este exprimată mai mult, cu atât rezistența activă a circuitului este mai mică.
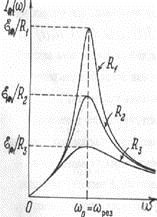
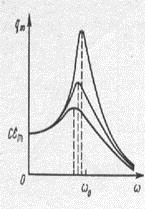
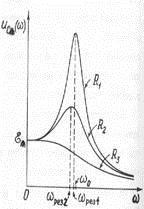
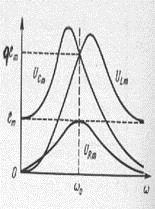
FIG.155 FIG.156 FIG.157 FIG.158
Valoarea maximă a tensiunii pe inductor (vezi § 51) este de asemenea transformată folosind conceptele de frecvență naturală și coeficient de amortizare:
. Frecvența de rezonanță poate fi găsită luând derivatul de frecvență al acestei expresii și echivalând-o cu zero. Frecvența de rezonanță pentru tensiunea pe inductor este :.
Dacă convertiți și comparați expresiile pentru frecvențele rezonante pe condensator și pe inductor cu o frecvență de rezonanță a curentului :. . . atunci putem concluziona că, în general, frecvența rezonantă pentru tensiunea pe condensator este întotdeauna mai mică, iar tensiunea pe inductor este întotdeauna mai mare decât frecvența de rezonanță a curentului (și tensiunea la rezistența activă). Curbele de rezonanță pentru tensiunile rezistenței active, inductorului și capacității sunt prezentate în Fig.
Pentru circuite de interes practic cu atenuare redusă. membru poate fi neglijat. În acest caz, rezonanța pentru toate variabilele de cantități electrice: curentul, sarcina și tensiunea pe condensator, tensiunea pe inductor vine aproape simultan la o frecvență a sursei egală cu frecvența oscilațiilor libere din circuit:
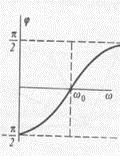
. La rezonanță, schimbarea de fază între curent și tensiune este zero (figura 159).
Pentru circuite cu atenuare mare, dacă rezistența activă este atât de mare încât. radicandul devine imaginar, iar curba de rezonanță nu are maximum, adică nu există rezonanță. În acest caz, dependența, de exemplu, de tensiunea condensatorului la frecvența sursă este prezentată în figura 157 pentru rezistența R3.
Fenomenul de rezonanță considerat la o conexiune consecutivă a unei surse cu elemente ale unui contur este numit rezonanța tensiunilor. În acest caz se numește impedanța de undă sau caracteristică, iar tensiunile maxime pe inductor și condensator sunt egale și opuse în fază.
Pentru circuitele cu atenuare scăzută, rezonanța "ascuțită" și factorul Q ridicat sunt caracteristice. care (vezi § 50) caracterizează scăderea relativă a energiei circuitului într-o perioadă cu oscilații libere.
Sensul fizic al Q pentru circuite cu atenuare redusă la rezonanță.
1) Factorul Q indică de câte ori valoarea maximă a amplitudinii de tensiune pe condensator (și pe inductor) depășește amplitudinea EMF extern (figura 158). .
În consecință, trebuie luat în considerare faptul că la rezonanță, chiar și cu un mic EMF extern, tensiunile de inductanță și capacitate pot atinge o valoare mare, care este periculoasă pentru viața umană:
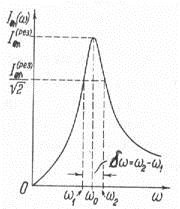
2) Se poate demonstra că factorul de calitate caracterizează lățimea relativă a curbei de rezonanță :. Lățimea curbei rezonante sau lățimea de bandă se numește intervalul de frecvență. limitată de frecvențe și. pe care amplitudinea este mai mică decât amplitudinea la rezonanță (figura 160).
Prin urmare, factorul de calitate este reciproc al lățimii relative de transmisie sau al lățimii relative a curbei de rezonanță.
Rezonanța este utilizată pentru a extrage din semnalul complex (tensiunea înregistrată) componenta dorită. Acest lucru are o importanță practică în domeniul radiotehnicii atunci când se recepționează și se ajustează la o anumită frecvență a unui semnal radio. Cu cât este mai mare factorul de calitate al circuitului, curba deja rezonantă și cu atât este mai ușor să se "reconstruiească" din transmisiile efectuate la frecvențele învecinate.
În practică, factorul Q al circuitului este, de asemenea, selectat ținând cont de calitatea necesară a recepției semnalului, deoarece, odată cu scăderea lățimii curbei de rezonanță, informațiile (domeniul de frecvență) "sarită" de către circuit scad.