Până acum am discutat algoritmul de învățare în care a fost activat un singur neuron de Kohonen pentru fiecare vector de intrare. Aceasta se numește metoda de acreditare. Precizia sa este limitată, deoarece ieșirea este complet o funcție a unui singur neuron din Kohonen.
În metoda de interpolare, un întreg grup de neuroni Kohonen cu cele mai mari randamente poate transmite semnalele sale de ieșire către stratul Grossberg. Numărul de neuroni dintr-un astfel de grup ar trebui selectat în funcție de sarcină și nu există date convingătoare despre dimensiunea optimă a grupului. Odată ce un grup este definit, setul său de ieșiri NET este considerat ca vector al cărui lungime este normalizată la una prin împărțirea fiecărei valori a NET cu rădăcina pătrată a sumei pătratelor de valori NET din grup. Toți neuronii din afara grupului au ieșiri zero.
Metoda de interpolare este capabilă să stabilească potriviri mai complexe și poate oferi rezultate mai precise. Cu toate acestea, nu există date convingătoare care să permită compararea modurilor de interpolare și acreditare.
Proprietățile statistice ale rețelei instruite
Metoda de predare Kohonen are o abilitate utilă și interesantă de a extrage proprietăți statistice dintr-o varietate de date de intrare. După cum se arată Kohonen [8], pentru probabilitatea de rețea pe deplin instruit că un vector de intrare selectat în mod aleatoriu (în conformitate cu funcția densitate de probabilitate a setului de intrare) va fi cel mai apropiat de orice vector de greutate dat este 1 / k, unde k - numărul de neuroni Kohonen. Aceasta este distribuția optimă a greutăților pe hipersferă. (Aceasta presupune că utilizați toți vectorii de greutate, care are loc numai în cazul dacă utilizați una dintre metodele discutate distribuția greutății.)
Învățarea stratului Grossberg
Stratul Grossberg este relativ ușor de învățat. Vectorul de intrare, care este ieșirea stratului Kohonen, este alimentat în stratul neuron Grossberg, iar ieșirile stratului Grossberg sunt calculate ca și în cazul funcționării normale. Mai mult, fiecare greutate este corectată numai dacă este conectată la un neuron Kohonen care are o ieșire nonzero. Valoarea corecției greutății este proporțională cu diferența dintre greutatea și ieșirea necesară a neuronului Grossberg cu care este conectat. Într-o înregistrare de caractere
unde ki este rezultatul neuronului Kohonen (numai pentru un neuron Kohonen este nenul), yj este componenta jth a vectorului de ieșiri dorite.
Inițial, este egal cu
0,1 și apoi scade treptat în procesul de învățare.
De aici se poate observa că greutățile stratului Grossberg se vor converti la valorile medii ale ieșirilor dorite, în timp ce greutățile stratului Kohonen sunt instruite la valorile medii ale intrărilor. Învățând stratul Grossberg se învață cu profesorul, algoritmul are ieșirea dorită, conform căreia este instruit. Învățând fără un profesor, stratul de auto-organizare al Kohonen oferă puncte de vânzare în poziții nedeterministe. Acestea sunt mapate la ieșirile dorite de stratul Grossberg.
Rețeaua de distribuire este complet
În Fig. 4.4 reprezintă rețeaua de contra-propagare în ansamblu. În modul normal de funcționare, vectorii de intrare X și Y sunt prezentați, iar rețeaua instruită furnizează vectorii X 'și Y' la ieșire. care sunt aproximări pentru X și Y, respectiv. Vectorii X și Y sunt presupuși aici ca vectori de unitate normalizați, prin urmare, vectorii generați la ieșire vor avea tendința de a fi normalizați.
În procesul de învățare, vectorii X și Y sunt alimentați simultan atât ca vectori de rețea de intrare, cât și ca semnale de ieșire dorite. VectorX este folosit pentru învățarea rezultatelor. și vectorul Y pentru învățarea ieșirii Y a stratului Grossberg. Rețeaua de distribuire este complet instruită folosind aceeași metodă ca cea descrisă pentru rețeaua de acțiune directă. Neuronii lui Kohonen acceptă semnalele de intrare ca vectori. și din vectori. Dar acest lucru nu poate fi distins de situația în care există un vector mare format din vectorii X și Y. și nu afectează algoritmul de învățare.
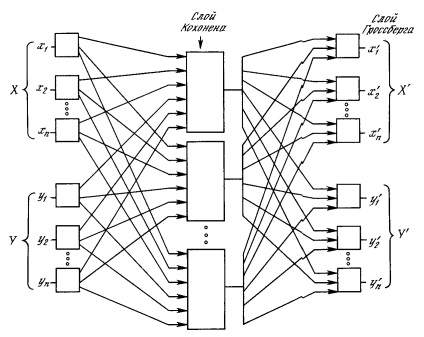
Fig. 4.4. Rețea completă de distribuție completă
Ca rezultat, se obține o singură mapare, în care prezentarea unei perechi de vectori de intrare generează copii la ieșire. Acest lucru nu este deosebit de interesant dacă nu observăm că prezentarea numai a vectorului X (cu vectorul Y egal cu zero) generează ambele ieșiri X '. și ieșiri Y '. Dacă F este o funcție de cartografiere X în Y '. atunci rețeaua se apropie de ea. De asemenea, dacă F este inversibilă, atunci prezentarea numai a vectorului Y (echivalent cu zero) generează X '. Abilitatea unică de a genera o funcție și inversul acesteia face ca rețeaua de contra-propagare să fie utilă într-o serie de aplicații.
Fig. 4.4 spre deosebire de configurația inițială [5] nu demonstrează un contracurent în rețea, prin care ia primit numele. Acest formular este ales pentru că ilustrează și rețeaua fără feedback și ne permite să generalizăm conceptele dezvoltate în capitolele anterioare.