Calculăm lucrarea, folosindu-se de această dată nu a doua lege a lui Newton. ci o expresie explicită a forțelor de interacțiune dintre corpuri, în funcție de distanțele dintre ele. Acest lucru ne va permite să introducă conceptul de energie potențială - energie care nu depinde de vitezele organelor, și distanțele dintre corpurile (sau distanțele între părți ale aceluiași organism).
Calculăm mai întâi lucrarea de gravitate atunci când corpul (de exemplu, o piatră) cade vertical în jos. La momentul inițial, corpul se afla la o înălțime h1 deasupra suprafeței Pământului și, în ultimul moment al timpului - la o altitudine de h2 (figura 6.5). Modul pentru mutarea corpului.
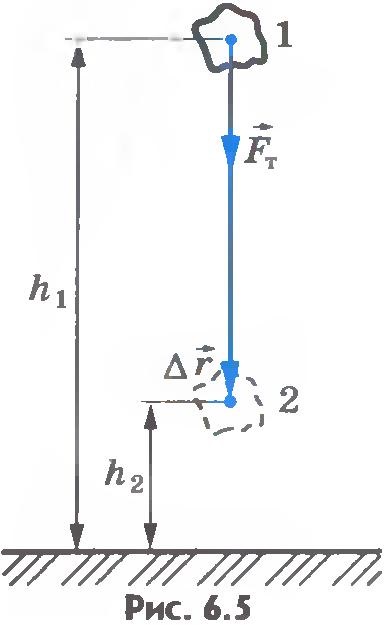
Direcțiile vectorilor de gravitate și deplasare coincid. Conform definiției lucrării (a se vedea formula (6.2)), avem
Acum, corpul să fie aruncat vertical în sus de la punctul situat la înălțimea h1, deasupra suprafeței Pământului, și a ajuns la înălțimea h2 (Fig.6.6).
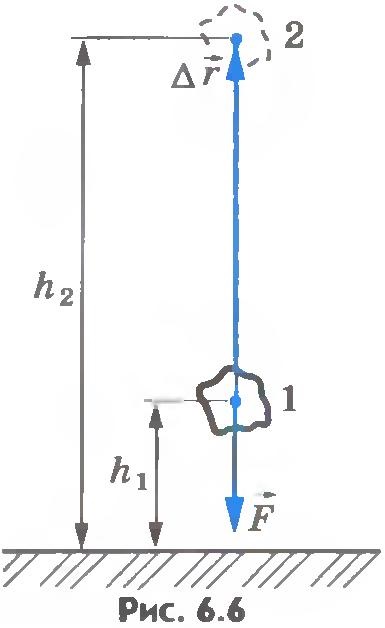
Vectorii sunt direcționați în direcții opuse și modulul de deplasare. Lucrarea de gravitate poate fi scrisă după cum urmează:
Dacă corpul se deplasează de-a lungul unei linii drepte astfel încât direcția de mișcare să formeze un unghi cu direcția gravitației (figura 6.7), atunci lucrarea de gravitație este egală cu:
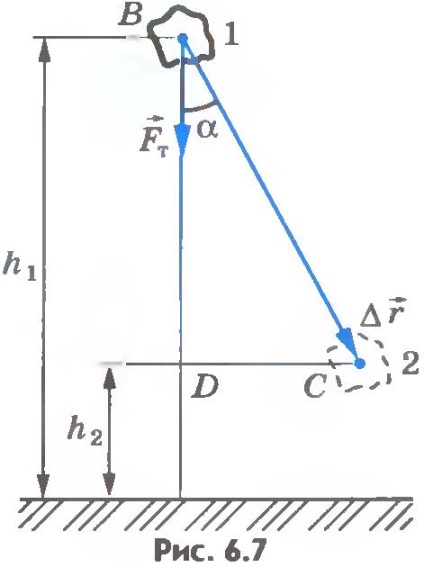
Din triunghiul dreptunghiular BCD se vede că. Prin urmare,
Formulele (6.12), (6.13), (6.14) fac posibilă observarea unei regularități importante. În cazul mișcării rectilinii a corpului, lucrarea de gravitație în fiecare caz este egală cu diferența a două valori ale cantității, în funcție de pozițiile corpului la momentele inițiale și finale ale timpului. Aceste poziții sunt determinate de înălțimile h1 și h2 ale corpului deasupra suprafeței Pământului.
În plus, lucrarea de gravitație atunci când se deplasează un corp de masă m dintr-o poziție în alta nu depinde de forma traiectoriei de-a lungul căreia se mișcă corpul. Într-adevăr, în cazul în care corpul se mișcă de-a lungul curbei BC (ris.6.8), apoi introducând acest lucru ca o linii curbe în trepte alcătuite din secțiuni verticale și orizontale de lungime mică, vedem că în gravitație de lucru orizontală este zero, deoarece forța perpendiculară deplasării , iar suma lucrărilor pe secțiuni verticale este egală cu munca pe care gravitatea ar fi făcut-o atunci când corpul sa deplasat de-a lungul unui segment vertical cu lungimea h1-h2.
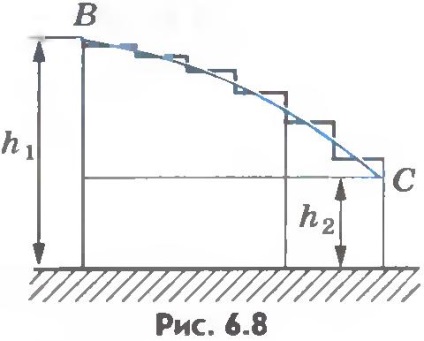
Astfel, lucrarea atunci când se deplasează de-a lungul curbei BC este:
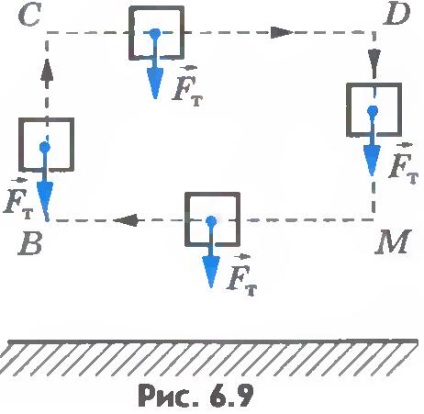
Când corpul se deplasează de-a lungul unei traiectorii închise, lucrarea de gravitație este zero. De fapt, permiteți corpului să se deplaseze de-a lungul conturului închis al VSDMB (Fig.6.9). Pe secțiunile BC și DM gravitația efectuează o activitate egală în valoare absolută, dar opusă semnului. Suma acestor lucrări este zero. În consecință, forța forței de gravitație pe întregul contur închis este zero.
Forțele care posedă astfel de proprietăți sunt numite conservatoare.
Deci, munca gravitațională nu depinde de forma traiectoriei corpului; este determinată numai de pozițiile inițiale și finale ale corpului. Când corpul se deplasează de-a lungul unei traiectorii închise, lucrarea de gravitație este zero.
O listă completă de subiecte despre fizică. un plan calendaristic pentru toate disciplinele în conformitate cu curriculum-ul școlii, temele, cursurile și o sarcină fizică pentru clasa a 10-a
Dacă aveți corecții sau sugestii pentru această lecție, scrieți-ne.
Dacă doriți să vedeți alte ajustări și dorințe pentru lecții, consultați aici - Forumul educațional.