Pentru tija dată este necesar:
- determină poziția centrului de greutate;
- calcula momentele centrale ale inerției;
- să construiască un teren sectorial (pune polul la centrul de greutate al secțiunii);
- se calculează momentul static liniar sectorial;
- construiți schema principală a zonei sectoriale (puneți polul în centrul curbei);
- pentru a calcula momentul sectorial de inerție;
- calculați momentul de inerție cu torsiune pură;
- calcula caracteristica de torsiune flexurală;
- Notați ecuația diferențială a unghiurilor de răsucire și a condițiilor limită;
- calculați forțele interne din tijă și construiți diagramele (tija este împărțită în 4 secțiuni);
- Calculați tensiunile normale dintr-o secțiune periculoasă și plotați diagramele.
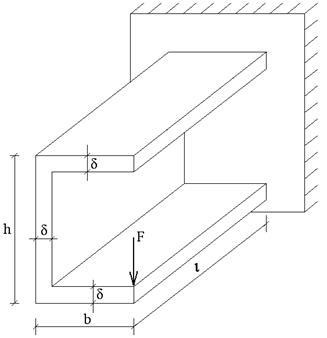
Schema numărul 1; punctul de aplicare a forței 2;
1. Împărțiți figura în protozoare, determinați aria dreptunghiurilor.
2. Determinați poziția centrului de greutate al secțiunii în raport cu axele
3. Calculăm principalele momente centrale ale inerției
4. Calculam aria sectorială.
Înlocuim canalul cu o schemă de proiectare care coincide cu liniile axiale ale secțiunii. Construim diagramele coordonatelor z și y.
Construim schema de sector sectorial (selectăm polul la centrul de greutate al secțiunii P = C). 0 este originea zonei sectoriale (la intersecția conturului cu axa de simetrie).
unde sunt coordonatele punctului de start al elementului;
- coordonatele punctului final al elementului.
Coordonatele 1 (4.04, 9)
punctele 2 (-9,46, 9)
față de 3 (4,04, -9)
centrul 4 (-9,46, -9)
gravitatea 0 (4,04, 0)
5. Determinați poziția centrului curbei.
În primul rând, se calculează momentele statice liniare sectoriale, pentru care înmulțim diagrama cu diagramele corespunzătoare ale coordonatelor (conform metodei lui Vereshchagin).
(înmulțirea diagramei simetrice cu un rezultat oblic simetric este 0).
Determinăm pozițiile centrului de îndoire.
6. Construiți diagrama zonei principale sectoriale (puneți polul în centrul curbei P = D). 0 este originea zonei sectoriale (la intersecția conturului cu axa de simetrie).
Coordonatele 1 (-5,5; 9)
față de 3 (-5,5, -9)
0 - principalul punct de nul Sectorial - cea mai apropiată de punctul de îndoire centrul de zero, la secțiuni cu o axă de simetrie este situat la intersecția conturului și axa.
7. Calculam momentul de inerție sectorial.
Pentru aceasta, multiplicăm diagrama cu graficul. (conform metodei Vere-
Shchagin și formula lui Simpson).
8. Calculați momentul de inerție pentru torsiune pură
9. Calculam caracteristica de torsiune flexurală
Mai întâi calculam modulul de forfecare:
10. Ecuația diferențială a unghiurilor de răsucire
- intensitatea externe de încărcare la torsiune distribuit, ținând cont de semnul (semnul „plus“ atunci când sarcina tinde să se rotească invers acelor de ceasornic atunci când este privit din direcția axei x pozitiv)
Condițiile arbitrare depind de condițiile limită
Noi scriem condițiile limită
Pentru capătul liber ()
Pentru un capăt ()
11. Calculați forțele interne. Calculăm calculele într-un tabel.
Cuplu cu torsiune liberă
Moment torsional cu torsiune constrânsă
În cazul unei forțe concentrate care acționează asupra tijei, trebuie îndeplinită următoarea condiție în toate secțiunile: