Linia elicoidală cilindrică 1) este o curbă tridimensională a aceleiași linii de pante. Punctul sculei, care atinge suprafața unei tije cilindrice rotative uniform, lasă o urmă pe ea sub forma unui cerc. Cu toate acestea, dacă, pentru a informa scula de mișcare uniformă de translație de-a lungul axei cilindrului, se obține o linie elicoidală cilindrică pe suprafața cilindrului.
În Fig. 301 prezintă formarea unei linii elicoidale pe suprafața cilindrului 2) de la mișcarea punctului A de-a lungul generatoarei CE și de la mișcarea de rotație a acestui generator. Iată câteva poziții ale acestui generator: E0 C0. E1, C1. ;
1) În caz contrar helis - de la helice (fr.) - o spirală, o linie elicoidală.
2) Această imagine a unui cilindru circular drept a fost luată în considerare în cursul unei școli secundare.
cu arce E0 El. E1 E2. sunt egale una cu cealaltă și fiecare este egală cu - πd / n. unde d este diametrul cilindrului și n este numărul de diviziuni (în figura 301 n = 12). Poziția inițială a punctului este notată cu A0. următorul - prin A1. A2 și așa mai departe.
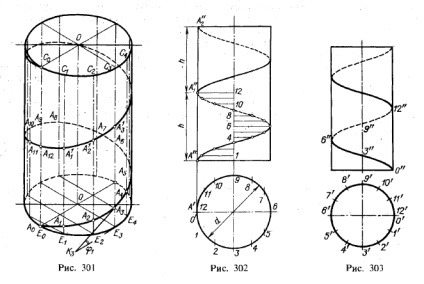
Dacă mutați imaginile din poziția E0 C0 pentru a poziționa punctul E1 C1 ia poziția de segment A1 E1 A1 determină distanța pe care punctul a trecut printr-un generator de la poziția sa inițială. În poziția ulterioară a generatoarei (E2 C2) se ridică la o înălțime de un punct E2 = A2 A1 și 2E1 t. D. Atunci când imaginea este făcută o revoluție completă, punctul se va deplasa de-a lungul-o la o distanță E0 2O = 12E1 A1.
Cu rotația suplimentară a generatorului, punctul A începe să formeze o a doua bobină. sau rotația spiralei. ocupând pozițiile A 1 1. A 1 2, etc.
Distanța dintre punctele A0 și A12 se numește pitch helix. Pasul poate fi ales în funcție de diferite condiții.
Distanța dintre punctul A și axa 00 se numește raza liniei de helix. iar axa 00 este axa liniei elicoidale. Raza liniei de șurub este egală cu jumătate din diametrul cilindrului circular drept, pe suprafața laterală a căruia există o linie de șurub. Două cantități - diametrul cilindrului și mărimea pasului - sunt parametrii 1) care determină linia cilindrică a șurubului de pe suprafața laterală a unui cilindru circular drept.
În Fig. 302, proiecțiile unei linii elicoidale cilindrice sunt construite. Proiecții preconstruite (așa cum au fost discutate în cursul școlii secundare), un cilindru drept circular. Circumferința bazei cilindrului (pe proeminența orizontală) și treapta (segmentul h, așezat de-a lungul axei cilindrului pe proiecția frontală) sunt împărțite în același număr (n) de piese; în Fig. 302, n = 12. Poziția inițială a punctului A este indicată de proeminențele A "și A" este punctul marcat de litera O 'de pe cerc.
1) Parametru (de la parametron (greacă) - măsurare) - o valoare ale cărei valori numerice vă permit să selectați un anumit element din numărul elementelor de același tip.
Deoarece axa cilindrului este direcționată perpendicular pe pătrat. π1, proiecția orizontală a liniei elicoidale fuzionează cu cercul. care este o proeminență orizontală a suprafeței cilindrului. În ceea ce privește construcția; proiecția frontală a liniei elicoidale, cursul construcției sale este clar din Fig. 302 și rezultă din însăși formarea liniei elicoidale ca o traiectorie a unui punct realizând două mișcări - uniforme de-a lungul unei linii drepte și în același timp rotative uniforme pe o axă paralelă cu această linie dreaptă.
Proiecția pe un plan paralel cu axa cilindrului, în acest caz proiecția frontală a unei linii elicoidale cilindrice, este similară cu un sinusoid.
În Fig. 302, proiecția frontală a liniei elicoidale are o creștere de la stânga la dreapta sau spre stânga pe partea frontală (vizibilă) a cilindrului; Dacă axa cilindrului este poziționată orizontal, linia de helix merge spre stânga și coborârea spre dreapta. Aceasta este o linie de șurub cu virajul drept. sau linia dreaptă a șuruburilor. Linia de înșurubare cu rândul din stânga (linia de șurub din stânga) este prezentată în Fig. - ridicarea pe proiecția frontală a liniei de șurub pe partea frontală (vizibilă) a cilindrului
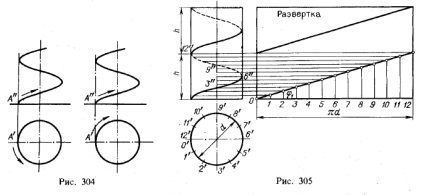
de la dreapta la stânga, coborâre spre dreapta; dacă axa cilindrului este poziționată orizontal, apoi creșterea spre dreapta și coborârea spre stânga.
Dacă linia elicoidală este reprezentată fără cilindru și fără proiecții de puncte, indicarea dacă linia de șurub este dreaptă sau stângă trebuie să fie dată fie printr-o inscripție, fie prin săgeți, așa cum se arată în Fig. 304 din stânga pentru linia dreaptă a șurubului, din dreapta pentru șurubul din stânga 1).
Dezvoltarea bobinei liniei elicoidale cilindrice este prezentată în Fig. 305. În forma extinsă, fiecare rotire este un segment de linie dreaptă. Acest lucru rezultă din formarea helix: ca circumferința bazei cilindrului împărțit într-un număr egal de părți și o spirală pas divizat în același număr de părți egale, matura o linie elicoidală peste pitch poate fi privit ca locul geometric al punctelor pentru fiecare dintre care ordonata este proporțională cu abscisa, adică, y = kx. Și aceasta este ecuația unei linii drepte. Tangentele de pe linia șuruburilor coincid în maturitate cu linia dreaptă în care se desfășoară bobina liniei elicoidale.
În Fig. 305 în două trepte ale spiralei, două segmente ale acestuia s-au obținut la un unghi φ1 la linia dreaptă, care este cercul expandat al bazei cilindrului. Abruptitatea ridicării liniei elicoidale este exprimată prin formula
1) Linia elicoidală cilindrică este bine ilustrată printr-un arc elicoidal, cu șuruburi filetate, șuruburi, știfturi, vierme cilindrice.
unde h este pasul spiralei și d este diametrul cilindrului. Unghiul φ1. se numește unghiul spiralei.
Lungimea unei rotații ("bobină") a helixului este L = √ (h 2 + (πd) 2).
Pentru aceeași d, valoarea unghiului φ1 depinde numai de pasul spiralei; pentru a obține un unghi mic de urcare, ar trebui să faceți un pas mic și invers. Dacă pasul rămâne neschimbat pentru cilindri de diferite diametre, atunci unghiul de ascensiune va fi mai mic, cu atât diametrul cilindrului este mai mare.
Modelul de linie elicoidală poate fi construit dacă luăm un dreptunghi cu o diagonală trasată pe el și îl rostogolim sub forma unui cilindru circular drept; în timp ce diagonala dreptunghiului formează o întoarcere a spiralei. Este evident că linia de șuruburi este cea mai scurtă distanță dintre două puncte de pe suprafața unui cilindru circular - linia geodezică a acestei suprafețe.
Într-adevăr, pot fi trase multe linii între cele două puncte de pe suprafața unui astfel de cilindru. Una dintre aceste linii oferă cea mai mică distanță între puncte. Atunci când o suprafață este desfășurată, o astfel de linie este desfășurată pe o linie dreaptă. Acest lucru este inerent în liniile de pe suprafață, numite geodezice.
Luați în considerare următoarea proprietate a unei spirale cilindrice.
Să presupunem că o linie tangentă intersectează spirala într-un anumit punct A3. π1 la punctul K3.
Unghiul dintre linia elicoidală și orice generator al cilindrului este exprimat de unghiul dintre această generație și tangenta (la linia elicoidală) trasată într-un punct comun pentru helix și formare. Măsurarea din Fig. 305 arată că se obține un unghi constant între această linie de șurub și generatoarele cilindrului, adică toate tangentele pe linia elicoidală sunt înclinate în mod egal față de generatoarele cilindrului și intersectează pătratul. π1 la același unghi φ1. Același unghi a fost obținut între șanțurile liniei elicoidale și circumferința bazei.
Când se aplică suprafața laterală a unui cilindru cu o linie elicoidală, de exemplu, elementul A0 A3 E3 (Figura 301) are forma unui triunghi dreptunghiular K3 A3 E3. în care K3 A3 este tangentă la helix la punctul A3. și K3 E3 - proiecția tangentei pe planul bazei cilindrului, adică tangenta la cercul bazei sale. Rezultă că punctul K3 aparține involuntare cercului, deoarece tangentele din toate punctele liniei elicoidale cilindrice au urme pe planul bazei cilindrului care formează contravaloarea bazei acestui cilindru.
Noi folosim acest lucru pentru a construi o tangentă la o linie elicoidală în oricare dintre punctele sale. Pe linia șurubului prezentată în Fig. 306, construit în punctul de tangență K. Mai întâi desenați o proiecție orizontală a tangentei - K'1 segment „- perpendicular pe O'K“. La punctul 1 ', proiecția 1 "se găsește pe valvă, după care se poate trasa proiecția frontală a liniei tangente 1" K ".
Este posibil să se construiască pe suprafața unui cilindru o linie curbată formată în același mod ca o linie elicoidală, dar să se lase rotația generatorului de uniformă a cilindrului și să se deplaseze punctul de-a lungul generatorului pentru ao face variabilă prin unele legi. Astfel de curbe sunt uneori numite linii cu șurub variabil.
Construcția este dată în Fig. 307 cu o mișcare uniform accelerată a punctului de-a lungul generatorului. Punctele sunt deplasate în fiecare dintre cele douăsprezece poziții marcate ale generatorului; de exemplu, la poziția nouă, punctul se va muta în segmentul C9 E9 (numărând din a opta poziție a acestui punct).
În Fig. 307 este de asemenea dată o scanare a liniei construite; unghiul ascensiunii.
Dacă punctul se deplasează uniform de-a lungul generatoarei conului circular drept 1), iar generatorul efectuează o mișcare de rotație în jurul axei conului,
1) Imaginea conului de pe desenul de proiecție a fost luată în considerare în cursul desenării liceului.
viteza unghiulară constantă, apoi traiectoria punctului este o linie elicoidală conică 1); proiecțiile sale sunt prezentate în Fig. 308. Deplasările punctului de-a lungul generatorului sunt proporționale cu deplasările unghiulare ale acestui generator. În Fig. 308 observat
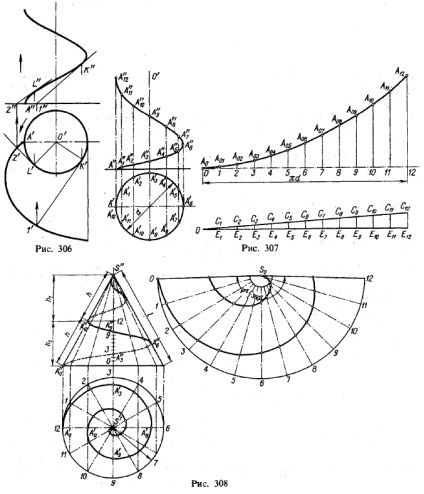
Pe suprafața conului există douăsprezece poziții ale generatorului, iar pozițiile corespunzătoare ale punctului sunt indicate pe ele. Distanța dintre punctele turnurilor adiacente A0 A12 = h, măsurată de-a lungul generatorului, se numește pasul liniei elicoidale conice 2)
1) Linia conică a șuruburilor este bine ilustrată, de exemplu, cu un arc conic elicoidal sau cu fir conic.
2) Uneori, pasul liniei elicoidale conice este socotit de-a lungul axei sale. Segmentul h1 (Figura 308) este proiecția etapei h, măsurată de-a lungul generatorului, pe axa spiralei. Divizarea lui h în n părți egale corespunde divizării lui h1 în părți egale egale unul cu celălalt și invers.
Proiecția unei linii elicoidale conice pe un plan paralel cu axa conului (în acest caz proiecția frontală) este un sinusoid cu o înălțime a valurilor în scădere; Proiecția pe un plan perpendicular pe axa conului (în acest caz proiecția orizontală) este spirala lui Archimedes.
Pe exteriorul alezorul conică (Fig. 308), spirala dreapta, de asemenea, se desfășoară într-o spirală de Arhimede, ca o deplasare unghiulară uniformă a razei la suprafața de scanare a conului corespunde deplasării uniforme a punctului de pe raza. Figura arată matura pentru două rotații ale elicei conice.
O linie elicoidală poate fi construită nu numai pe o suprafață cilindrică sau conică. Un exemplu este o linie elicoidală (figura 309) pe o suprafață formată din a
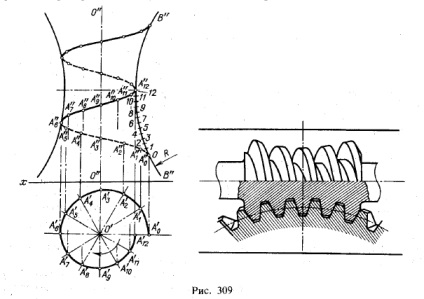
prin rotirea arcului BB în jurul axei 00, adică pe suprafața torului 1). O linie similară de șurub poate fi observată pe viermi globoid (vezi Figura 309, dreapta).
Întrebări la § 48
- Cum se formează liniile elicoidale cilindrice și conice?
- Care este treapta liniei elicoidale - cilindrice și conice?
- Ce fel de proiecții ale liniilor elicoidale cilindrice și conice pe planuri - paralele cu axa liniei elicoidale și perpendiculare pe această axă?
- Cum să recunoaștem dacă linia de șurub dreapta sau stânga este aplicată pe suprafața tijelor cilindrice și conice? Cum pot specifica un accident vascular cerebral dacă este tras doar o linie?
- Care este evoluția fiecărei bobine a liniei elicoidale cilindrice și conice?
- Cum crește înălțimea helixului?
- Care linie este formată pe un plan perpendicular pe axa spiralei cilindrice, dacă sunt construite urmele de tangente la această linie?
1) Informația despre torus este furnizată în cursul școlii secundare.