

Proiectul este prezentat de studenții unui colegiu de transport auto: MaloletnevEvgeniy, Novikov Alexey și KosterevIvan. Studiind știința calculatoarelor, am observat că este strâns legată de matematică. În sala de clasă am aflat ce descoperiri în domeniul matematicii au dus la apariția computerelor, fără de care nu reprezentăm existența noastră contemporană. În activitatea noastră am vrut să vă familiarizăm cu aceste descoperiri.


Ne-am propus să urmărim istoria apariției numerelor și sistemelor numerice. Am fost curioși cine stă la sursa sistemului de numere binare, cât de mult timp și de unde a început să fie folosit, de ce sistemul numeric binar a supraviețuit până în ziua de azi.


În primele etape ale dezvoltării societății, oamenii aproape că nu știau cum să conteze. Un număr mare de subiecte pe care le-au combinat în conceptul de "mult". Nu era un cont, era doar fătul lui.
Foarte important a fost instrumentul natural al omului - degetele lui. Acest instrument nu a putut stoca rezultatul contului pentru o lungă perioadă de timp, dar a fost întotdeauna "la îndemână".


Conceptul de "număr" este cheia atât pentru matematică, cât și pentru informatică. Oamenii au luat mult timp în considerare și au înregistrat numere. Dar le-au înregistrat în conformitate cu reguli diferite. Numărul a fost reprezentat utilizând unul sau mai multe simboluri, numite numere.


În vremurile străvechi, numerele erau notate cu notații rectilinie ("bastoane"); Un stick a reprezentat unitatea, două bastoane - deuce. Acest mod vine de la crestături pentru a înregistra ultimele zile.
Primele cifre scrise, despre care avem dovezi fiabile, au apărut în Egipt și în Mesopotamia cu aproximativ cinci mii de ani în urmă.


Din numărul degetului, începutul sistemului de numere din cinci cifre (o mână), zecimal (două mâini), douăzeci (degete și degete de la picioare).
Ulterior, a apărut noțiunea de număr. Un sistem numeric este un sistem de reguli care vă permit să setați
corespondența dintre orice număr și reprezentarea acestuia. Setul de simboluri folosit pentru o astfel de reprezentare este numit numere.


În antichitate, multe popoare nu au comunicat între ele, prin urmare diferite popoare aveau sisteme diferite de numere. Oamenii au ajuns la o decizie sensibilă - să scrie numerele în funcție de categorii: unități separate, separat zeci, separat sute.
Deci, au existat sisteme de numere pozitive. În sistemul cu număr de poziționare, valoarea cifrei este determinată de poziția sa în număr.


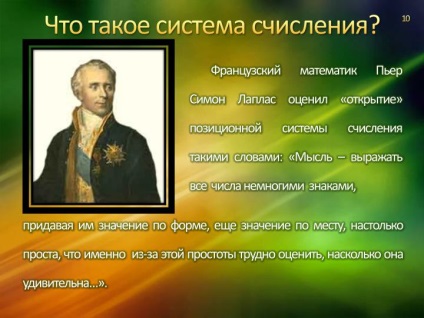
Matematicianul francez Pierre Simon Laplace a estimat "descoperirea" sistemului de numere poziționale cu aceste cuvinte: "Ideea este de a exprima toate numerele cu câteva semne,
oferindu-le importanță în formă, încă importantă în loc, este atât de simplă încât din cauza acestei simplități este dificil de a evalua cât de uimitor este ... ".



Ca un om care-i place cultura chineză, Leibniz știa despre cartea Schimbărilor. Leibniz a fost interesat de inscripții criptice, pe care oamenii de știință chinezi nu le-au putut explica. Inscripțiile au constat dintr-o serie de linii lungi și scurte. De la vremuri străvechi până la zilele noastre, "Cartea schimbărilor" a avut o mare influență asupra întregii vieți a societății chineze.

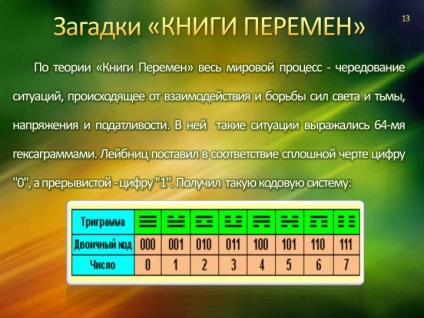
Conform teoriei "cărții schimbărilor", întregul proces mondial este o alternanță de situații, provenind din interacțiunea și lupta forțelor de lumină și întuneric, tensiune și randament. În ea, astfel de situații au fost exprimate prin 64 hexagrame. Leibniz a pus numărul "0" în linie cu linia solidă și "1" în linia întreruptă. Am primit un astfel de cod:

Descriind sistemul binar, Leibniz a aflat că există legi complet noi ale matematicii. El a notat simplitatea specială a algoritmilor de acțiuni în aritmetica binară în comparație cu alte sisteme. Regulile pentru efectuarea acțiunilor sunt specificate de tabelele de adăugare binară, scădere și multiplicare.


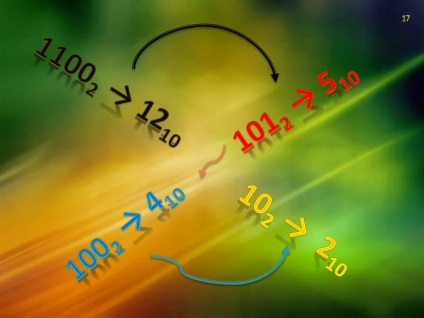
Medalia trasată de Leibniz, în 1697, explică relația dintre sistemele binare și zecimale ale calculului


Avea 1100 de ani
A intrat la clasa 101
Într-un portofoliu de 100 de cărți pe care l-am purtat
Toate acestea sunt adevărate, și nu prostii.
Când pulverizează o duzină de picioare,
A mers pe drum,
Catelul a alergat întotdeauna după ea
Cu o coadă, dar cu 100 de picioare
Înțelegea fiecare sunet
Cu urechile sale zece
Și zece mâini tăbăcite au servit o servietă și o leșie
Și zece ochi de culoare albastră s-au uitat în jurul lumii ca de obicei
Dar totul va deveni destul de obișnuit,
Când înțelegeți povestea noastră.



Punctul și linia erau cele mai elementare simboluri pe care le-ar fi putut transmite telegraful Morse. Acestea corespundeau impulsurilor scurte și lungi ale curentului electric, transmise prin cabluri telegrafice. Codul Morse atribuie fiecărei litere din alfabet o secvență de puncte și liniuțe.






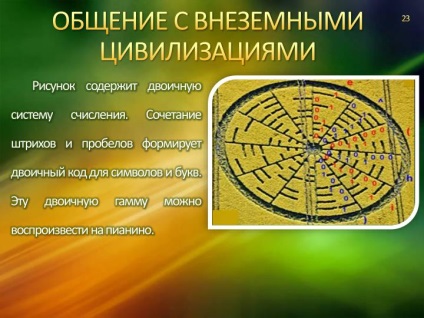
Icoana din Chilbolton a fost răspunsul la mesajul nostru pământesc. O pictogramă complexă reprezintă o tabelă de cod binar. În structură, repeta mesajul radio al pământeștilor.




Figura conține un sistem de numere binare. Combinația dintre curse și spații formează un cod binar pentru caractere și litere. Această scală binară poate fi reprodusă pe un pian.

Purtătorii de hârtie au fost cel mai convenabil mod de introducere a informațiilor. Primele cărți au fost folosite în războaiele lui Jacquard. Cifra este codificată de o gaură, litera -
două găuri. Ele au fost utilizate în mașinile de numărare până în 1980.

În supermarketurile de pe pachetele de bunuri puteți vedea codul de bare. Este necesar pentru introducerea informațiilor în casa de marcat. Scanerul percepe fiecare bară neagră ca o secvență de unități de lungime de la unu la patru, intervalele dintre benzi sunt ca zerouri. Grosimea benzilor poate avea patru valori - de la cele mai subțiri la cele mai groase.

Un tabel de numere binare poate fi ușor transformat într-un set de carduri pentru a ghici gândurile. La fiecare număr zecimal corespunde un cod binar.
Puteți face cinci cărți cu numere, în care fiecare coloană de numere este scrisă pe un card separat.

Trebuie să îi dai persoanei o carte și să ceri să te gândești la orice număr de la 0 la 31. Solicitați să returnați acele cărți pe care apare acest număr.
După ce ați primit cardurile, puteți numi imediat numărul planificat.


Studentul a făcut o estimare de 13. El a returnat trei din cele cinci cărți, cu acest număr. În fiecare carte, ia în considerare primul număr, în care sunt 4, 8, 1. Rezumați-le și obțineți o estimare: 4 + 8 + 1 = 13. Și așa numărul 13 pe care elevul la gândit sa dovedit. Experiența a avut succes.
Fiecare număr conceput specifică o combinație specială.

Proiectul calculatorului care lucra într-un sistem binar a fost prezentat de Leibniz într-o lucrare scrisă în 1679. El a încercat să aplice codul binar în mecanică și a făcut un desen al unui computer care a lucrat pe baza noii matematici. Dar, în curând, a realizat că posibilitățile tehnologice ale timpului său nu permit crearea unei astfel de mașini.

Un rol deosebit în istoria civilizației îl joacă inventarea computerelor electronice, pe care noi le numim calculatoare. Primele computere s-au bazat pe sistemul de numere zecimale, dar mai târziu și-au amintit despre sistemul binar.
Care este avantajul acestui sistem de numere?

- Primele computere binare au fost construite pe principiile stabilite de John von Neumann. În computere, codurile zero și unitate sunt reprezentate de semnale electrice în două state.

Aparatul matematic al algebricii logice sa dovedit a fi foarte convenabil pentru a descrie modul în care funcționează hardware-ul calculatorului. Sistemul de numere de bază din computer este binar, în care sunt folosite cifrele 1 și 0, iar valorile variabilelor logice sunt de asemenea două:
"1" și "0". Creatorul algebrului logicii este John Bull. Cu ajutorul algebrei booleene, se poate construi o diagramă a unui automat care lucrează pe un releu.

Una dintre cele mai avansate calculatoare releu a fost mașina RVM-1, proiectată și construită sub supravegherea inginerului sovietic N. I. Bessonov la mijlocul anilor '50.

Datorită utilizării principiului cascadelor de efectuare a operațiunilor aritmetice, inventat de Bessonov însuși, mașina a produs până la 1.250 de multiplicări pe minut. Acesta conținea 5500 de relee. O serie de îmbunătățiri și-au îmbunătățit fiabilitatea și performanța atât de mult încât a funcționat până în 1965.

36 au verificat modul în care funcționează
Lumea calculatorului devine din ce în ce mai complicată în fiecare an. Puterea calculatoarelor este dublată la fiecare 18 luni. Calculatoarele personale pe care elevii joacă astăzi sunt mai puternice decât supercomputerele din trecutul recent. Sunt lansate tot mai multe sisteme de operare productive, apar noi domenii de aplicații informatice.

Concluzia a verificat modul în care funcționează

Guter R.S. Polunov Yu.L. - De la abacus la computer (Biblioteca cunoasterii) - 1981
Fomin S.V. Sistemul numerelor. M. Nauka, 1987.
Reshetnikov V.N. Sotnikov A.N. Informatică - ce este? M. Radio și comunicare, 1989.
