LECȚIA 11. Mișcarea corpurilor cerești. Forțele de maree.
1. Mișcarea perturbată.
2. Problema cu trei corpuri.
3. Teoria mareelor.
4. Forțele de maree în cosmonautică.
1. Mișcarea perturbată.
Problema fundamentală a mecanicii cerești - problema n corpurilor este după cum urmează. În vid există n puncte materiale care interacționează în conformitate cu legea gravitației universale. Având în vedere pozițiile inițiale și vitezele de puncte, este necesar să găsim poziția oricăror astfel de organisme în orice moment arbitrar. Pentru un arbitrar n problema nu a fost rezolvată până acum. Deși sunt dezvoltate metode pentru rezolvarea numerică a acestei probleme pe computere. Aceste metode ne permit să găsim poziția oricărui punct cu o precizie dată la orice interval de timp finit. Dar aceste metode nu pot răspunde la întrebarea despre comportamentul punctelor pe un interval de timp infinit. Anume, această întrebare este extrem de importantă pentru înțelegerea soarta sistemului solar și a întregului univers.
Soluția problemei pentru n egală cu una și două este dată de Newton. Pentru n = 2, această mișcare este de-a lungul orbitelor de la Keplerian în jurul centrului comun de masă. Această mișcare corespunde soluției problemei cu două corpuri. numit neperturbat. De fapt, toate corpurile sistemului solar sunt atrase nu numai de Soare, dar și de fiecare alte. Prin urmare, niciun corp din sistemul solar nu se poate deplasa exact de-a lungul unei elipse, parabole sau hiperbola, și chiar mai mult pe circumferință. Deviațiile în mișcarea corpurilor din legile lui Kepler sunt numite perturbații, iar mișcarea reală a corpurilor este o mișcare înfruntată. Perturbările corpurilor sistemului solar sunt foarte complexe, deși sunt de dimensiuni mici, deoarece masa totală a tuturor corpurilor perturbatoare este de 700 de ori mai mică decât masa Soarelui.
Să considerăm un exemplu de sistem cu trei corp ca o forță tulburătoare îndreptată. Să fie trei corpuri cerești: Soarele cu o planetă cu o masă M. P1 cu m1 masa la o r1 distanta de centrul Soarelui și P2 planeta cu m2 masă la insistențele lui R2 de la Soare, la o distanță r de planeta P1. Toate cele trei organisme se comportă reciproc în conformitate cu legea lui Newton. Într-un sistem de referință inerțial asociat cu centrul de masă al Soarelui este accelerat în direcția CP1 planetei P1 și accelerația CP2 în direcția P2 planetei. Heliocentrică proceda în cadru non-inerțial de referință, adică ia în considerare mișcarea planetei P1 în raport cu Soarele. În acest caz, planeta P1 se va aplica forța determinând accelerarea următoarele: direcția PC1. în direcția P1P2 și în direcția paralelă cu P2C.
Prima accelerare w este accelerarea mișcării relative cauzată de atracția Soarelui; este responsabil pentru mișcarea planetei P1 în jurul Soarelui (și nu în jurul centrului comun al masei) conform legilor lui Kepler. Accelerațiile w și w constituie accelerația forței perturbatoare și provoacă abateri în mișcarea planetei P1 din legile lui Kepler. În consecință, în cazul examinat, forța de perturbare constă în două forțe: de la forța de acțiune a planetei P2 la planeta P1 și de forța de acțiune a planetei P2 de pe Soare. Concluzie: accelerarea de la perturbație este diferența în vectorii accelerațiilor cauzate de corpul perturbant de pe planetă și de Soare. Din figură se poate observa că, în cazul general, forța de perturbare nu este direcționată exact spre corpul perturbator P2.
2. Problema cu trei corpuri.
Soluția exactă a problemei mișcării cerului pentru cazul a trei corpuri și mai mult în general, adică forma de formule finite care fac posibilă calcularea cu exactitate a poziției în spațiu și viteza tuturor corpurilor în orice moment este, în principiu, imposibilă. O soluție generală pentru trei corpuri, sub formă de rânduri infinite, a fost găsită în 1912 și este practic imposibil de utilizat acum. În prezent, sarcinile mișcării corpurilor cerești sunt rezolvate prin metode numerice
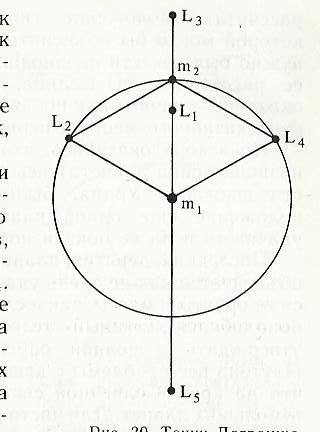
Una dintre cele mai interesante soluții ale problemei a fost găsită de Lagrange pentru așa-numita problemă limitată cu trei corpuri. Se referă la mișcarea unui sistem cu trei corpuri a cărui mase sunt legate de relația: m1 >> m2 >> m3. În acest caz, cel de-al doilea corp se deplasează de-a lungul orbitei lui Kepler, iar al treilea corp se află în unul dintre cele cinci puncte Lagrange. Mișcarea la punctele L1. L3. L5 este instabil, iar la punctele L2 și L4 - stabil: cel de-al treilea corp, lovind unul dintre aceste puncte, va fi permanent. Sistemul solar are loc similar corpurilor cerești cauzate în mod natural, de exemplu, două grupuri de asteroizi, care se mișcă de-a lungul pe orbita lui Jupiter Lagrange punctul L2 și L4 acestuia. În viitor, utilizarea punctelor Lagrange de om în Pământ - Luna, care va fi amplasat sateliți releu pentru a asigura o comunicare continuă între Pământ și stațiile lunare situate pe partea din spate a Lunii.
3. Teoria mareelor.
De două ori pe zi în mări și oceane există o creștere și cădere de apă. Deja în vremuri străvechi, observatorii au observat că valul apare ceva timp după culmea Lunii în locul de observare. În plus, mareele sunt deosebit de puternice în zilele de lună nouă și plină, adică Când centrele Pământului, Luna și Soarele sunt situate aproximativ pe o linie dreaptă. Având în vedere acest lucru, Newton a explicat curentul prin acțiunea forțelor gravitaționale din partea Lunii și a Soarelui.
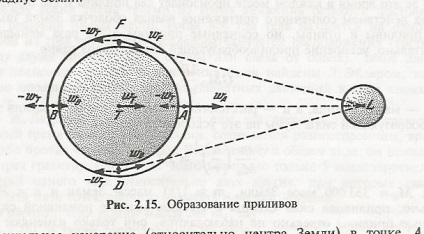
Să scriem expresiile pentru accelerațiile create de atracția Lunii pentru diferite puncte ale Pământului (atracția Pământului nu este luată în considerare încă). Sistemul de referință inerțial asociat cu centrul de masă al Pământului - Luna, valori ale accelerației sunt determinate prin formulele: în care Wa, wT, wV - accelerația cauzată de atracția lunii în punctele A, T, V; M este masa lunii; r este raza Pământului; R este distanța dintre centrele Pământului și Lună (R 60 r).

este necesar să se scadă accelerația centrului pământului de la valorile tuturor accelerațiilor.
Urmați pașii din paranteze, și să ia în considerare faptul că r este mică și poate fi neglijată. Apoi, în idim că mareelor de accelerație opusă și îndreptată departe de centrul Pământului. Accelerația care apar într-un cadru de referință asociat cu corpul, datorită faptului că, din cauza dimensiunii finite a corpului diferitelor părți ale diferitelor corp perturbant sunt trase, numite accelerare mareelor iobratno rasstoyaniyado proporțională cu cubul corpului perturbant, iar forțele de putere nazyvayutsyaprilivnymi corespunzătoare.
La punctele A și B, accelerația gravitației g este mai mică decât norma, iar la punctele F și D, în care forțele rezultate sunt direcționate mai aproape spre centrul pământului. Presiunea apei din ocean la aceeași distanță față de centrul Pământului ar trebui să fie aceeași. Presiunea coloanei de apă este determinată de expresia P = gh. Este clar că înălțimea coloanei h ar trebui să fie mai mare în acele locuri unde accelerarea scăderii libere este mai mică, unde greutatea coloanei de apă este mai mică și viceversa. Deci, la punctele A și B se ridică deasupra nivelului mediu de apă, formând o cocoasa așa-numita mareelor pentru egalizarea presiunii, iar punctele F și D vor fi mai mici decât în mod normal, se observă la aceste fenomene puncte maree.
De fapt, imaginea este chiar mai complicată, deoarece Pământul se rotește în jurul axei sale mult mai rapid decât Luna obbegat în jurul valorii de ea, astfel încât umflătura mareelor se misca prin suprafața Pământului, în timp ce restul de tot timpul în fața lunii. În timpul dintre două culminații succesive Moon egale cu o medie de 24 h 52 m. By-pass cocoașe mareei din întreaga lume, în fiecare locație va avea loc la doi și doi ebb tide.
P
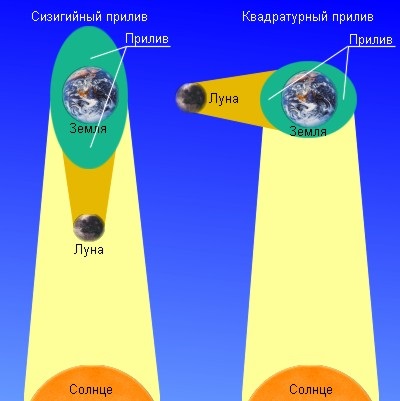
Luna este bufeuri nu numai oceanele, dar în scoarța și atmosfera Pământului. Sub influența forțelor de maree, litosfera se întinde pe o jumătate de metru. Frecarea apei împotriva partea de jos, precum și deformarea Pământului solid însoțită de eliberare de căldură, ceea ce duce la o scădere a Pământului energie mecanică - sistem Moon, adică încetini rotația Pământului ... În fiecare secol, durata zilei crește cu aproximativ 0,002 s. Cu două miliarde de ani în urmă, durata Zilei Pământului a fost de numai 10 ore, iar în viitorul îndepărtat, acestea vor fi egale cu o lună. Deja acum, datorită forțelor mareice ale Lunii cu care se confruntă Pământul este în mod constant aceeași parte, adică. E., Atunci când Luna se rotește la o viteză diferită, iar strămoșii noștri au văzut partea din spate a lunii, dar luna este mult mai mică decât Pământul, ea a oprit repede. Mai mult decât atât, puncte de atracție proiecții de maree care abate asupra luna datorită rotației rapide a Pământului, luna trage de-a lungul orbitei înainte, prin care acesta este îndepărtat de pe pământ, la o viteză de 3 cm pe an, se deplasează într-o orbită mai mare.
4. Forțele de maree în cosmonautică
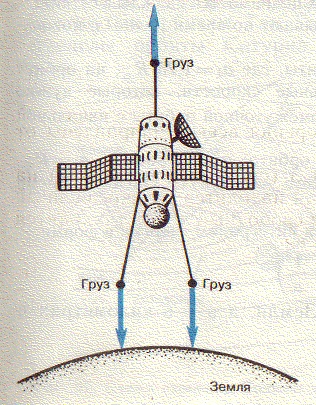
Moțiunea de sateliți artificiali pământ (AES) are loc în conformitate cu legile mecanicii cerești, dar nu întotdeauna este posibil să se ia în considerare un punct material, astfel încât, în unele cazuri, este necesar să se ia în considerare acțiunea forțelor de maree. accelerația Tidal dispuse simetric în raport cu centrul de satelit al punctelor gravimetrice situate pe aceeași linie cu centrul Pământului, în semn opus și sunt egale cu: în cazul în care un - modul de accelerare a mareelor; h este înălțimea satelitului de deasupra Pământului; l este proiecția deviației unui punct dat de centrul de greutate al satelitului până la centrul liniei Pământului, centrul de greutate al satelitului. Accelerațiile în mișcare sunt întotdeauna îndreptate departe de centrul de greutate al satelitului; toate lucrurile pe care le-ai lăsat să le atârni în spațiul satelitului mai devreme sau mai târziu vor fi la margini. Să calculam un exemplu concret. Lăsați la distanță de 3 m de centrul de greutate al satelitului un obiect neatasat. Mișcarea unui obiect în timpul zborului liber al unui satelit este determinată numai de microaccelerațiile create de forțele de maree. Înlocuind datele cunoscute (l = 3, m, g = 9,8 m / s 2. R = 6378 * 10 6 m), obținem accelerația totală a mareelor de 10 -5 m / s 2. Dar chiar și cu o astfel de accelerare mică a subiectului în zece minute va fi de aproximativ 2 m mai aproape de corpul satelitului decât a fost. Să verificăm. Distanța d. care trece prin corp în timp t. având accelerația a și viteza inițială zero este :. Prin urmare, este practic imposibil să se realizeze o greutate totală în satelit.
Dar, uneori, forțele de maree joacă un rol pozitiv. Astfel, pentru mulți sateliți este necesar să se mențină o anumită orientare față de Pământ. De exemplu, sateliții meteorologici efectuează un studiu continuu al capacului nor al Pământului. Firește, obiectivele echipamentelor prin satelit trebuie să fie întotdeauna direcționate spre Pământ. Pe măsură ce forțele mareice ale Pământului de miliarde de ani, a stabilit o parte a Lunii pe Pământ, la fel cum se desfășoară și laterale sateliți corect pe Pământ, dar, desigur, mult mai rapid. Acest lucru se face după cum urmează. Bilele lungi și ușoare sunt atașate la sarcini mici. Forțele de maree care acționează asupra acestor sarcini vor deschide satelitul astfel încât tijele să fie amplasate de-a lungul razei Pământului. Aceasta va asigura orientarea dorită a satelitului.
1. Cum vor diferi perioadele de revoluție ale sateliților artificiali ai Pământului și ale Lunii dacă acești sateliți se află la distanțe egale față de centrele lor?
2. Calculați masa Marte în comparație cu masa Pământului din mișcarea satelitului său Phobos, pentru care a = 9300 km, T = 0,32 zile.
3. Luna la apogee este de 1/9 mai mult decât perigeul. Cât de multe procente la forța de maree perigee este mai mare decât la apogeu?
Întrebări ale sondajului rapid.
1 Ce este mai mult: accelerația raportată de Pământ la Soare sau pe Pământ raportată Lunii?
2. De ce sunt cele mai mari valuri la vremea lunilor pline și a lunilor noi?
3. De ce este imposibil să atingem zero gravitație într-un satelit artificial pământ?
4. Cum se mișcă Pământul sub influența forțelor de maree?
5. Cum sunt forțele de maree îndreptate către centrul Pământului?
6. Care faze ale lunii sunt cele mai mici valuri de pe Pamant?
7. Ce este o mișcare neperturbată?
8. De ce nu continuă fluxul și debitul în 12h, dar 12h. 26min.?
9. Ce caracteristică a corpurilor celeste ne permite să calculăm a treia lege a lui Kepler?
10. De ce Luna întotdeauna se confruntă cu Pământul cu o singură parte?
11. De ce se realizează sarcini de stabilizare pe satelit pe bare lungi?