Rezistența de intrare a circuitului în raport cu ramura k este definită ca raportul dintre emf. Ek. acționând în această ramură, la actualul Ik din aceeași ramură sub emf. în ramurile rămase egale cu zero
Conductivitatea de intrare a ramurii k este reciprocă a rezistenței de intrare a acestei ramificații
Rezistența mutuală (rezistența de transfer) a ramurilor k și l este raportul dintre emf. Ek. care acționează în ramura k. la actualul Il. trecând de-a lungul ramurii l la emf. în ramurile rămase egale cu zero
Conductibilitatea reciprocă a ramurilor k și l este reciprocitatea rezistenței reciproce a acelorași ramuri
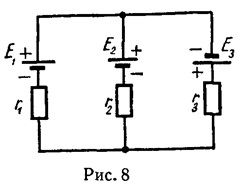
Un exemplu. Pentru circuitul din Fig. 8, rezistența de intrare a circuitului față de ramurile 1, 2 și, respectiv, 3 este egală cu
iar rezistențele reciproce ale ramurilor 1 și 2, 2 și 3, 3 și 1 sunt, respectiv, egale
Pentru orice circuit electric închis suma puterii dezvoltate de sursele de energie electrică, este suma puterii consumate în receptoarele de energie
unde EI este suma algebrică; Aici, acele termeni pentru care liniile de acțiune ale emf sunt pozitive sunt pozitive. E și curentul corespunzător I coincid, în caz contrar, termenul este negativ (când direcțiile pozitive ale curenților din ramurile de a alege emf coincizând direcție curent cu acțiunea FME corespunzătoare); I 2 r - suma aritmetică; Aici trebuie luate în considerare atât rezistențele externe, cât și rezistențele surselor de energie.
Exerciții și sarcini
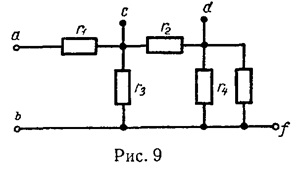
Calcularea rezistenței rab.
Se constată rezistența echivalentă a rezistențelor r4 și r5 conectate în paralel prin formula (14)
este conectat în serie cu r2; rezistența lor totală
Rezistența circuitului constă în rezistența r1. în serie cu care două rezistențe paralele r 'și r3
Calcularea rezistenței rcd.
Rezistențele r4 și r5 sunt acum conectate în paralel una cu cealaltă; rezistența r3 la ele este conectată în serie
Rezistența la diferentiala se compune din două rezistențe legate în paralel, R2 și r »și încă
Calcularea rezistenței rdf.
Rezistența echivalentă a circuitului dintre punctele d și f constă din trei rezistențe conectate paralel: r5. r4 și r2 + r3 și poate fi determinată prin formula (13)
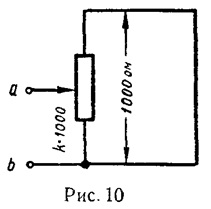
Problema 2. Pentru circuitul (figura 10) trageți o curbă de rezistență echivalentă între punctele a și b în funcție de k (0 ≤ k ≤ 10).
Problema 3. Circuitul prezentat în Fig. 11, a. constă din cinci rezistențe identice r1 = r2 = r3 = r4 = r5 = 10 kΩ.
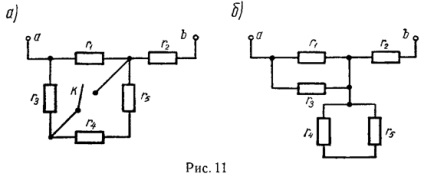
Care este rezistența circuitului dintre bornele a și b cu tasta deschisă și închisă K?
Rezistența r3. r4 și r5 sunt conectate în serie; rezistența echivalentă echivalentă este paralelă cu rezistența r1; valoarea rezistenței care înlocuiește r3, r4. r5 și r1. este
Rezistență necesară la circuit
În acest caz, rezistențele r1 și r3 sunt conectate în paralel unul cu altul, iar rezistențele r4 și r5 sunt scurtcircuitate (fig.11, b). Rezistența necesară a circuitului va fi
Sarcina 4. Se calculează rezistența echivalentă a circuitului (Fig. 12), între bornele a și b. dacă toate cele șapte dintre rezistențele sale sunt aceleași:
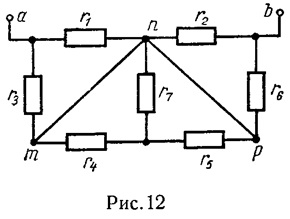
Notă. Acordați atenție conductorilor de scurtcircuitare mn și np.
Când cheia este deschisă, circuitul dat poate fi reprezentat conform Fig. 13, b.
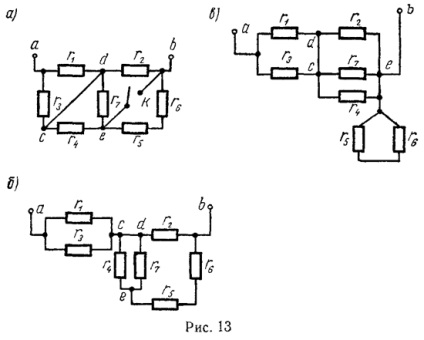
Cu o cheie închisă, circuitul dat are forma prezentată în Fig. 13, c.
Rezistența circuitului este egală cu suma a două rezistențe
și r ". determinată prin formula
din care r '= 3,33 ohmi. În acest fel,