Dacă desenați un cerc coardă paralelă cu diametrul său, mijlocul acestor acorduri aparțin diametre perpendiculare. Mijlocul coardelor, paralel cu al doilea diametru, face parte din primul diametru. La comprimarea două cerc cu diametrul perpendicular sunt afișate în două diametre ale elipsei, care se numesc conjugate. Două direcții paralele cu direcțiile diametrelor conjugate se numesc conjugate.
Dacă coardele paralele cu un diametru de diametrul diferit elipsă împărțit în jumătate, iar corzile sunt paralele cu un diametru al elipsei, împărțit în jumătate primul diametru.
Aceste două diametre sunt diametrele conjugate ale elipsei. Fiecare diametru corespunde unui conjugat cu diametru complet definit. Diametrele principale (axele) ale elipsei sunt atât diametre perpendiculare cât și conjugate.
Acum să trasăm două raze perpendiculare OA și OB într-un cerc. Ca rezultat al compresiei, ele trec în două conjugate semidiameter OA1 = elipsă a1 și b1 = OB1 (vezi. Fig. 21).
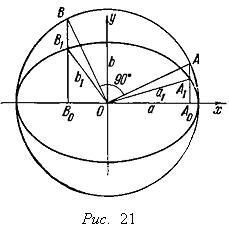
unde A0 și B0 sunt proiecțiile punctelor A și B pe axa de compresie și a este coeficientul de compresie. Dar din egalitatea triunghiurilor OAA0 și OBB0 rezultă că OA0 = BB0. OB0 = AA0. prin urmare
de unde, după înlocuirea valorii lui k, găsim:
Diametrele conjugate ale elipsei, direcțiile conjugate, diametrele principale (axele) elipsei.