cunoscutul astronom american S. Nuke (1835-1909) a dovedit matematic imposibilitatea de a crea aeronave mai grele decât aerul.
Dacă întrebi un pasager de ce zboară avionul, el răspunde cu voce tare: în cer (pentru ce). Și va fi greșit - după cum vom vedea, avionul zboară ... pe pământ!
În primul rând, să ne amintim o problemă bine cunoscută. Pe cântare sunt două cutii opace. În una dintre ele se află o muște, în alta - aceeași zbura zboară. Ce vor arăta scalele? Răspunsul este zero. Deoarece o muscă zburătoare, pentru a rămâne în aer, creează un curent de impuls, exact egal cu greutatea sa. Acest flux de impuls (flyweight), îndreptat în jos, este transmis la partea de jos a cutiei, echilibrând zbura așezată în cealaltă cutie.
Poate că nu toată lumea înțelege care este fluxul de impuls? Apoi, ia în considerare un alt exemplu.
Elicopterul arata ca un elicopter care plutea in aer. Ce îi permite să nu cadă? Șurubul "suge", aerul care este în repaus ("la infinit") este în repaus (v ∞ = 0) = 0 \ right)>. și o aruncă la o viteză de v. Desigur, acest aer devine mai devreme sau mai târziu în locul său, astfel încât elicopterul creează un vortex toroidal, amestecând întreaga atmosferă, așa cum este arătat (calitativ) în Fig.
Dacă notăm densitatea aerului prin care p kg / m³ (la viteze subsonice și densitatea de flux poate fi considerată constantă), masa de aer care curge într-o unitate de timp printr-o secțiune de viteză S v. este egal cu μ = ρ v S [kg / m³ ⋅ m / s ⋅ m2 = kg / s].
Ne amintim derivarea acestei formule. Debitul Q [m³ / s] este volumul de lichid sau gaz care curge prin secțiunea transversală a fluxului sau țevii pe unitate de timp: Q = Δ V Δ t >>.
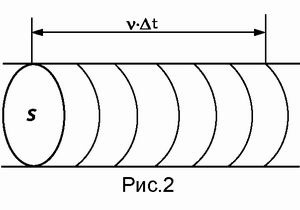
Fie S suprafața secțiunii transversale a fluxului, v viteza sa. Apoi, volumul Δ V = s ⋅ v ⋅ Δ t trece prin intervalul de timp Δ t prin secțiunea transversală s (figura 2). Atunci Q = ΔV Δt = s ⋅ v> = s \ cdot v> și μ = ρ ⋅ Q = ρ ⋅ s ⋅ v. Această cantitate poate fi numită în mod natural fluxul de masă. Și dacă o împărțim în zona secțiunii transversale a debitului, obținem densitatea de debit masic μ S = ρ v> = \ rho v> [kg / (m² ⋅ s)]
Întrebați de ce terenul este aici și veți avea dreptate - FĂRĂ NICIUNE.
Acum înclinați planul șurubului elicopterului "înainte" (Fig.3)
Descompune forță de tracțiune pe componenta verticală și orizontală X. Y Elicopterul zboară în direcția forței X, componenta Y, desigur, trebuie să rămână în greutate egală, iar X este echilibrată de forța de rezistență a aerului. În rol de avion în crearea acestor două forțe sunt împărțite: aripa creează o (ridicare) rezistența verticală și cu motor - tracțiune. (Detalii la: „a crea o rezistență verticală aripă (de ridicare)“ - dar cum?) Și aripa are o proprietate remarcabilă: este capabil de a crea o forță de ridicare este mult mai mare decât forța de rezistență a aerului la propunerea. Un fizician ar spune - un ordin de mărime mai mare. Aceasta, desigur, nu înseamnă „exact 10 ori mai mult,“ - poate fi de 8 și 20. Raportul dintre aceste două forțe se numește aripa de calitate Y X = K> = K>. Prin urmare, spre deosebire de aeronave elicopter cu aripi are nevoie de o forță forță la ordinul de greutate la mașină (și, de fapt, chiar și pentru o planare elicopter staționare ar trebui să aibă o forță de ridicare de cel puțin greutate - chiar și cu atât mai mult pentru deplasarea pe orizontală).
Timp de aproximativ o jumătate de secol, avioanele au folosit forța de propulsie a elicei. Avioanele moderne folosesc motoarele cu reacție. Dar principiul fizic este același: orice motor trebuie să creeze un flux de impuls.
Să estimăm cu ce viteză motorul avionului ar trebui să arunce înapoi greutatea gazului. În cazul în care greutatea aeronavei este calitatea aripa G, K, și vom folosi motoarele N, fiecare dintre ele este de a crea o forță de tracțiune G / KN. Mai mult, în cazul în care producția de densitatea gazului suprafața motorului secțiunii S este ρ s> viteza de evacuare v, fluxul de masă într-un sistem de coordonate asociat aeronavei, μ = ρ sv S.> \ Rho _ >>>> [kg / s] . Vom presupune aproximativ că este egal cu debitul de masă la intrarea în motor. Acest lucru înseamnă că ignorăm greutatea suplimentară de combustibil ars - rolul acesteia din urmă, prin urmare, este vorba în jos pentru a încălzi aerul, și nu la o creștere a debitului masic - și un consum mai mic de combustibil, motor de aeronave mai economic. Apoi, ca urmare a încălzirii aerului care curge prin motor, viteza sa (și acest lucru se datorează faptului că, după cum știm, impulsul specific) este crescută prin V-u, în care u - viteza de zbor (Fig.4).
Astfel, variația impulsului (iar acest lucru este un motor de tracțiune) este F 1 = μ (vu) = ρ su S (vu) = G / K N. = \ mu (vu) = \ rho _us ( vu) = G / KN.> presupunem ca presiunea gazului la ieșirea motorului este exact egală cu presiunea aerului ambiant (indice ∞), iar temperatura lor este Ts. Apoi densitatea se găsește din legea lui Mendeleev-Clapeyron: ρ s = p ∞ / R T s. = P_ / RT _,> unde R = R 0 / M / M> - constant de gaz, R 0 = 8 31 = 8,31> J / K ⋅ mol, M = 29 ⋅ 10-3> kg / mol - molar masa aerului. Apropo, avem grijă ca densitatea gazelor de eșapament ρ s> să nu fie egală cu densitatea atmosferei, care este accentuată de indicele s.
Facem estimări numerice. Luați în considerare greutatea modernă avionului G = 400 T = 4 ⋅ 10 iunie HH> având N = 4 Motor raza r a secțiunii de ieșire de un metru, care zboară la viteze subsonice u = 250 m / s la o înălțime mai mare de 10 km, presiunea atmosferica de cinci ori mai mică presiune la nivelul mării, p ∞ = 10 5/5 = 2 ⋅ 10 4 = 10 ^ / 5 = 2 \ cdot 10 ^> Pa. Ce este Ts. Înlocuim aceste numere în ecuație
F = 1 p ∞ / RT sv π r 2 (vu) = G / KN = 4 ⋅ 10 6 / (4 ⋅ 10) Oct. 5 = H = P_ / RT_v \ pi r ^ (vu) = G / KN = 4 \ cdot 10 ^ / (10 \ cdot 4) = 10 ^ H>
Rezolvind această ecuație patratică (cu privire la v), găsim v ≈ 500 m / s.
Desigur, un astfel de motor (a cărui rază a secțiunii de evacuare a ordinii de metri), nu poate fi decât o linie transatlantică foarte mare. Dar de ce este profitabil să construim avioane mari? Acest lucru corespunde teoriei asemănării, care era cunoscută chiar în timpul lui Jonathan Swift. Aici el scrie despre acest martor Gulliver: „Matematica Maiestății Sale, pentru a determina înălțimea creșterii mele cu ajutorul unui cadran, și a constatat că această înălțime este în acest sens, la înălțimea unui pitic ca douăsprezece-unu, încheiat pe baza similitudinii corpurilor noastre, că volumul meu corpul este egal, cel puțin, cu volumul de 1728 de corpuri de liliputani și, prin urmare, necesită de câte ori mai multă mâncare ". Cu alte cuvinte, în cazul în care Lilliput se bazează pe un sandwich, atunci Gulliver - 12½ sandwich-uri. Este clar că aici se presupune că densitatea masică identică a corpurilor Lilliput și Gulliver.
Un alt lucru - avionul. După cum se poate observa din expresia (1), forța de ridicare este proporțională nu cu volumul, ci cu suprafața. Deci, dacă măriți dimensiunea caracteristică a aeronavei de N ori, volumul său va crește cu N3 ori, iar zona aripii și, în consecință, greutatea - în N2 ori. Acest lucru se datorează faptului că avionul este o cochilie, nu un corp solid. (Este clar că în aceste argumente ρ v 2> - așa-numitul cap de viteză - se presupune că este fixat).
Da, dar! - cititorul atent va exclama - după ce se recepționează formulele (1) pentru elicopter și deja vorbim despre avioane? Aici este necesar să se liniștească cititorul atent cu aceste cuvinte: Ai dreptate, dar dacă admitem că forța vântului care acționează asupra aeronavei, în funcție de care p densitatea [kg / m³], viteza v [m / c], și mărimea L [m ], singura combinație a acestor cantități care au o dimensiune de forță, se va p v 2 L 2 L ^> [kg / m³ ⋅ m / s² m² ⋅ ⋅ = m kg / s²]. Desigur, pentru a determina valoarea numerică a acestei forțe ar fi necesar să se ia în considerare, de asemenea, factorul de adimensională necunoscut - ci pentru că am fost interesați numai în relația de forțe și nu valoarea lor.
Deci, la ce înălțime avionul nu ar fi zburat, este pur și simplu obligat să creeze un puls de puls egal cu greutate, îndreptat în jos și, în final, să se aplece pe pământ.
Dar, desigur, nu este numai muște, elicoptere și avioane. Am discutat despre conceptul de flux și densități de flux sunt destul de comune în multe domenii ale fizicii. Acestea sunt concepte foarte utile. Probabil deja ghicit că puteți intra nu numai conceptul fluxului de masă și impuls, dar și alte mărimi fizice: fluxul de impuls unghiular (în cazul în care ceva se transformă), fluxul de energie, fluxul de sarcină electrică (de asemenea, cunoscut sub numele de amperaj), fluxul de inducție un câmp magnetic ... dar altceva altceva. Dar pentru prima dată a fost destul de spus.
Deci, dacă îi spui rudelor, prietenilor și cunoștințelor că viteza este un impuls specific, iar forța este un flux de impuls, veți avea absolut dreptate. Și dacă adăugați că presiunea este densitatea fluxului pulsului, veți fi foarte inteligenți în școală și, cu siguranță, veți intra în MIPT.
1. Estimați debitul minim (debitul masic) al combustibilului N μ T.> necesar pentru a asigura forța de tracțiune a aeronavei considerată în text. Când se arde un kilogram de combustibil, se eliberează energia r, J / kg (valoarea calorică). Considerați că această energie este folosită pentru a depăși forța de rezistență (puterea N F 1>) și pentru a modifica energia cinetică a gazelor (înainte și după trecerea motoarelor). Pierderea energiei termice este neglijată. Pentru kerosen, ia r = 40 MJ / kg.
2. Comparați consumul de combustibil cu consumul de aer.
3. Estimați zona aripilor avionului în cauză.