Volumul unei stări cuantice în spațiul de fază. Funcția densității stărilor de energie.
Pentru a calcula densitatea stărilor de energie pentru o particulă, calculăm mai întâi densitatea stărilor în spațiul reciproc (impuls sau k-spațiu). Distanța dintre stări este dată de condițiile limită. Pentru electronii și fotonii liberi într-o cutie cu dimensiunea L și pentru electronii dintr-o latură de cristal cu dimensiunea laturii L, folosim condițiile limită periodice Born-von Karman. Folosind funcția de undă a unei particule libere, obținem
2 \ pi n = kL \\
\ frac = \ Delta k \\
unde n este orice număr întreg, și \ Delta k \, este distanța dintre stările cu k diferite.
Numărul total de stări k disponibile pentru o particulă este volumul spațiului k accesibil, împărțit la volumul k-spațiului ocupat de o singură stare. Volumul disponibil este pur și simplu integrale de k = 0 la k = k. Volumul k-spațiului pentru o stare în cazul n-dimensional este scris în formular
g_s este degenerarea unui nivel (de obicei o degenerare de spin de 2). Această expresie trebuie diferențiată pentru a găsi densitatea stărilor în spațiul k: g (k) \, dk = \ frac \, dk. Pentru a găsi densitatea energetică a stărilor, este necesar să cunoaștem legea dispersiei pentru o particulă, adică să exprimăm k și dk în expresia g (k) dk în termeni de E și dE. De exemplu, pentru un electron liber: E = \ frac = \ frac, dE = \ frac \, dk.Cu o definiție mai generală,
unde indicele s corespunde unei stări de spectru discret sau continuu și delta este funcția delta delta. Când treceți de la sumare la integrare, ar trebui să utilizați regula
unde \ hbar este constanta lui Planck.
Idealul gazului Fermi. Relația dintre energia Fermi și concentrația electronilor.
Idealul gazului Fermi. Energia medie a unui electron.
Tipuri de legături de atomi și molecule în cristale. Stările amorfe și cristaline. Dulap de cristal. Perioadă Lattice. Stările electronilor dintr-un cristal. Conceptul de quasimoment.
Modelul Kronig-Penny. Funcția Wave a unui electron.
Modelul Kronig-Penny. Zonele energetice. Zonele Brillouin. Conectarea benzilor de energie și a nivelelor de energie ale unui electron într-un puț potențial cu pereți infinit de mari.
Clasificarea cristalelor prin structura benzilor de energie. Banda de conducere și banda de valență. Masa efectivă a unui electron și a unei găuri.
Determinarea semiconductorului intrinsec. Apariția conductivității electrice a unui semiconductor intrinsec din punctul de vedere al reprezentărilor modelului și al teoriei benzilor. Calcularea concentrației de electroni în banda de conducție a unui semiconductor arbitrar.
23. Determinarea semiconductorului intrinsec. Apariția conductivității electrice a semiconductorului intrinsec. Starea electroneutralității. Calcularea nivelului Fermi și a conductivității semiconductorului intrinsec. Graficele n = f (T), # 61555; # 61472; # 61501; # 61472; f (T); Ln # 61555; # 61472; # 61501; # 61472; f (1 / T). Determinarea experimentală a lățimii W3.
Ambele procese - generatoare de perechi de purtători și recombinarea lor - orice cantitate de semiconductoare au loc simultan. Concentrația purtătoare corespunzătoare se stabilește de la starea de echilibru dinamic, în care numărul de purtători emergente este egal cu numărul de recombinarea. Intervalul de timp dintre generarea suportului de încărcare și recombinarea sa se numește durata de viață a unui electron liber sau a unei găuri, iar distanța parcursă de un purtător în timpul unei vieți este calea medie liberă. Având în vedere că durata de viață a purtătorilor individuali este diferit în cadrul acestor termeni se înțelege durata medie de viață și drumul liber.
Nivelul Fermi este principalul parametru al distribuției statistice a electronilor și a găurilor. În calculele pentru a determina poziția nivelului Fermi, de regulă, se folosește condiția de electricitate.
Pentru un semiconductor intrinsec, n = p.
Când calculul concentrației intrinseci trebuie să ia în considerare dependența bandgap temperaturii (1.17). Concentrația intrinsecă este un parametru caracteristic important al materialului, deoarece pentru o temperatură dată, ni 2 este o constantă nu numai pentru materialele intrinseci, ci și pentru cele dopate (nu depinde de poziția nivelului Fermi). Valorile concentrației intrinseci pentru principalele materiale semiconductoare sunt prezentate în tabel.
24. Determinarea semiconductorilor donatori și a impurităților donatorilor. Conductivitatea electrică a unui semiconductor donator la temperaturi ridicate și joase. Temperatura epuizării impurităților. Starea electroneutralității. Graficele n = f (T), # 61555; # 61472; # 61501; # 61472; f (T); Ln # 61555; # 61472; # 61501; # 61472; f (1 / T). într-o gamă largă de temperaturi.
Donorul și impuritatea donatorului. Conductivitatea electrică a conductorului donator la temperaturi ridicate și joase. Condiții de electroneutralitate.
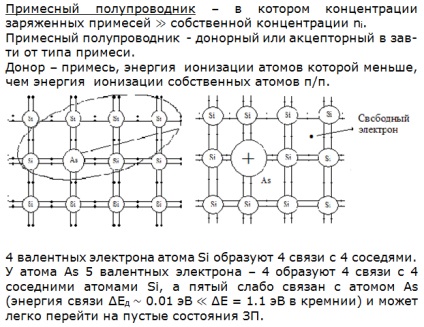


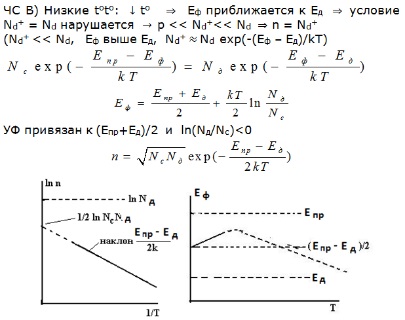
25. Calculul nivelului Fermi al unui semiconductor donator. Calcularea conductivității electrice specifice a unui semiconductor donator. Graficele n = f (T), # 61555; # 61472; # 61501; # 61472; f (T), Ln # 61555; # 61472; # 61501; # 61472; f (1 / T) într-un interval de temperatură mare.

Concentrația de echilibru. Relația dintre concentrațiile de electroni și găurile în semiconductori intrinseci și impurități. Efectul suprimării.
Să luăm în considerare cazul general când concentrația donatorilor mici diferă de concentrația de acceptori mici. Pentru claritate, presupunem asta. În acest caz, donatorii mici și acceptorii mici în cantitate vor fi compensați reciproc, adică toți acceptorii vor fi umpluți cu electroni proveniți din centrele donatoare, prin urmare. Numărul de donatori necompensați capabili să participe la generarea termică a electronilor în banda c va fi egal cu: - concentrația efectivă a donatorilor. Prin urmare, la un raport, semiconductorul se comportă ca un tip de semiconductori. Într-un astfel de semiconductor nu există găuri de impurități, dar există găuri formate ca rezultat al tranzițiilor intrinseci la temperaturi ridicate. Ecuația de electricitate pentru un astfel de semiconductor, luând în considerare secțiunea anterioară, va avea forma:
Să luăm în considerare câteva cazuri speciale.
1. Temperaturi foarte scăzute.
În acest caz. . Apoi ecuația de electroneutralizare ia forma:
Înlocuim (3) expresia pentru. obținem:
- concentrația de donatori ocupată de electroni.
- concentrarea efectivă a donatorilor ionizați.
O astfel de ecuație este rezolvată în §4.
Se vede că energia de activare.
3. Temperaturi ridicate.
În acest caz, nu putem neglija valoarea. . Apoi ecuația de electroneutralizare ia forma:
Soluția acestei ecuații în §5. La temperaturi ridicate:
În mărime. în acest domeniu, se poate determina o concentrație eficientă.
4. Temperaturi foarte ridicate.
27. Viteza de generare. Generarea termică. Rata de recombinare. Coeficientul de recombinare. Stări de echilibru și staționare. Concentrația excesivă. Legea scade concentrația în exces cu timpul. Durata de viață a transportatorilor minoritari. Graficele lui Dp (t). p (t) (sau Dn (t) .n (t).
Sub acțiunea tensiunii aplicate cristalului, în el apare un câmp electric. Se comandă mișcarea transportatorilor de sarcină: electronii se deplasează spre electrodul pozitiv, găurile către electrodul negativ. În același timp, mișcarea termică a purtătorilor de sarcină nu se oprește, în urma căruia apar coliziuni cu atomii din semiconductor și impuritățile.
Mișcarea direcțională a purtătorilor de sarcină sub acțiunea forțelor câmpului electric se numește derivație. Curentul provocat de această mișcare este un curent de derivație. În acest caz, natura curentului poate fi electronică, dacă este cauzată de mișcarea electronilor sau de gaura, dacă este creată de o deplasare dirijată a găurilor.
Viteza medie a suporturilor de încărcare într-un câmp electric este direct proporțională cu intensitatea câmpului electric:
M Coeficientul de proporționalitate se numește mobilitatea electronilor (mil) și găuri (mp). Electronii liberi se mișcă în spațiul dintre nodurile rețelei de cristal și găurile se deplasează de-a lungul legăturilor covalente, astfel încât viteza medie și, prin urmare, mobilitatea electronilor sunt mai mari decât găurile. Mobilitatea pe bază de siliciu a purtătorilor de sarcină este mai mică decât cea a germaniului.
În semiconductori intrinseci concentrațiile de electroni și gaura sunt aceleași, dar din cauza diferitelor mobilitatea lor a componentei electronice a curentului peste gaura. În semiconductori de impurități, concentrațiile de electroni și gauri sunt semnificativ diferite, natura curentului fiind determinată de purtătorii principali de încărcare: în semiconductori de tip p, găuri și în semiconductori de tip n de către electroni.
Cu o concentrație neuniformă a purtătorilor de sarcină, probabilitatea coliziunii lor este mai mare în acele straturi ale semiconductorului, unde concentrația lor este mai mare. Căldura termică haotică, purtătorii de încărcătură deviază de partea în care numărul de coliziuni este mai mic, adică se deplasează în direcția scăderii concentrației lor.
Mișcarea direcțională a purtătorilor de sarcină dintr-un strat cu o concentrație mai mare a acestora într-un strat în care concentrația este mai mică se numește difuzie. iar curentul cauzat de acest fenomen este un curent de difuzie. Acest curent, ca și curentul de derivație, poate fi electronic sau gaură.
Gradul de neuniformitate în distribuția purtătorilor de sarcină este caracterizat de un gradient de concentrație; este definit ca raportul dintre modificarea concentrației și variația distanței la care se produce. Cu cât mai mult gradient de concentrație, adică cu cât se schimbă mai mult, cu atât este mai mare curentul de difuzie.
Electronii, care se deplasează dintr-un strat cu o concentrație ridicată într-un strat cu o concentrație mai scăzută, se recombină cu găuri pe măsură ce progresează și invers, difuzând într-un strat cu o concentrație redusă a găurii, se recombină cu electroni. În acest caz, concentrația în exces a purtătorilor de sarcină scade.