Metodele directe utilizează câteva formule pentru a calcula cantități necunoscute într-un număr finit de etape în procesul de calcul
Un exemplu. Metoda inversă a matricei
Un neajuns esențial al metodelor directe este necesitatea de a stoca toate elementele n-pătrat ale matricei sistemului în memoria calculatorului, adică metodele directe nu iau în considerare în nici un fel structura descărcată a matricei în sisteme.
În plus față de această aplicare a metodelor directe pentru rezolvarea SLAE cu un număr mare de variabile duce la o acumulare semnificativă a erorilor de calcul.
Metodele bine cunoscute includ metoda Gauss, metoda de maturare.
Metodele iterative (metode de aproximare succesivă) sunt metode în care un lanț de soluții aproximative este construit folosind un algoritm
Fiecare ciclu de astfel de calcule se numește iterație.
Algoritmii iterativi sunt mai complicați decât metodele directe. Cantitatea de calcule necesare în timpul utilizării lor este dificil de determinat în avans, dar nu necesită păstrarea tuturor elementelor sale atunci când se lucrează cu matrice descărcate. În plus, ele folosesc adesea formulele computaționale care au stabilit aceste exemple. Procesul iterativ este structurat astfel încât erorile computaționale de la iterație la iterație să nu se acumuleze. Prin urmare, metoda iterativă poate fi folosită atât pentru a rezolva SLAU bine condiționată, cât și pentru o condiție slabă.
Exemple: Metoda simplă de iterație și metoda Gauss-Seidel
Metoda de eliminare Gauss
Este bine cunoscut faptul că algoritmul metodei Gauss pentru rezolvarea SLAE constă în doi pași principali.
Pe calea dreaptă prin eliminarea succesivă a variabilelor din ecuațiile sistemului, matricea sistemului duce la o formă triunghiulară.
soluția prin metoda de eliminare dă o matrice triunghiulară superioară:
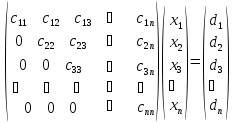
Pe cursul invers, soluția exactă a sistemului
înlocuiți în ecuația precedentă și obțineți:
Metoda Gaussiană este eficientă numai dacă matricea sistemului este bine condiționată, are un număr redus de condiționalități.
Precizia calculului depinde în mod semnificativ de modul în care elementul de conducere pe care îl folosim este folosit pentru a exclude variabilele în mișcarea înainte.
Un exemplu. Luați în considerare sistemul:
Luați ca element de conducere
La decizia noastră vom primi:
dacă este rotunjită, atunci aproximativ obțineți acest lucru greșit!
Acum, să luăm ca element de conducere coeficientul anterior din a doua ecuație, adică 1.
Apoi, dacă este rotunjită, obținem soluția corectă
Reguli pentru selectarea unui lider:
selectarea coloanei
Se consideră prima coloană. Se presupune că vrem să excludem. În această coloană găsim elementul maxim, adică Gasim ecuatia unde coeficientul este mare si noi rearanjam aceasta ecuatie in primul loc si folosim coeficientul ca element de conducere.
selectarea rândului
Din prima ecuație găsim o variabilă, pe care o vom exclude. Căutăm și căutăm în consecință, ceea ce corespunde acestui element maxim. Și puneți primul loc și excludeți-l.
Această tehnică poate fi generalizată pentru toate elementele
în întreaga matrice
Scanăm coloanele și liniile și le căutăm. Găsim și punem acest element în primul rând.
Această metodă este cea mai acceptabilă.
Metoda maturării este un caz special al metodei Gauss, care este special conceput pentru rezolvarea sistemelor de ecuații cu o matrice diagonală diluată
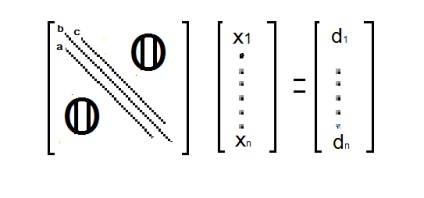
Cursul direct este că acești coeficienți
Procesul în sine este după cum urmează.
Cursa inversă corespunde calculului variabilelor în ordine inversă, începând cu cel mai recent x
știind, puteți găsi
În general, schema de metode iterative pentru rezolvarea SLAU este următoarea:
în alt mod este necesar să se stabilească o soluție inițială
calculați partea dreaptă:
găsim soluția sistemului de ecuații: - vectorul corecțiilor
de la punctul 5. mergeți la 2.
O întrebare importantă este când să oprim!
Ca oprire, utilizați orice inegalitate de vector care compară soluțiile obținute la iterația precedentă și ulterioară.