Rezistența la radiații este unul dintre parametrii principali ai unei antene de sârmă. Rezistența la radiații este coeficientul care conectează puterea radiației antenei și pătratul valorii curente a curentului.
Pentru calculul rezistenței la radiații se utilizează două metode:
1) metoda de integrare a vectorului de evaluare
2) metoda EMF indusă.
În ambele cazuri, rezistența la radiație este determinată de formula
unde este valoarea efectivă a curentului la care se referă rezistența. Cu toate acestea, metoda de determinare a puterii radiației antenei este oarecum diferită în fiecare dintre metodele de mai sus.
Luați în considerare esența metodei de integrare a vectorului Poynting și utilizarea acestuia pentru a calcula dipol. Ideea metodei este următoarea. Se presupune că antena în cauză este situată într-un spațiu liber nelimitat. Antena înconjurată mental de o suprafață închisă (de obicei, pe o rază de sferă mare), iar fluxul de putere este determinată de undele electromagnetice care trec prin sfera spus în spațiul extern. Deoarece se presupune că nu există pierderi în spațiul din jurul antenei, fluxul de putere este puterea de radiație a antenei:
Aici - valoarea numerică a vectorului Poiting, care determină puterea care trece printr-o singură zonă tangențială la suprafața sferei; pentru spațiu liber
unde este valoarea efectivă a intensității câmpului electric la amplasament.
Astfel, produsul determină fluxul de energie printr-o zonă elementară. iar integrarea în formula determină toată puterea de radiație a antenei.
Înlocuindu - se în. avem
Să calculăm rezistența la radiație a unui vibrator simetric subțire cu o distribuție de curent sinusoidal. Valoarea efectivă a intensității câmpului creată de un astfel de vibrator poate fi determinată folosind expresia
Luând în considerare faptul că în coordonatele sferice
Pentru un vibrator simetric nu depinde de el. Prin urmare, rezistența la radiații, referită la curentul de la antinod,
Integralul din partea dreaptă a ecuației nu este exprimat în funcție de funcțiile elementare. Integrarea, puteți obține următoarea expresie:
unde este sinele integral al argumentului; - cosinus integral al argumentului; este constanta lui Euler.
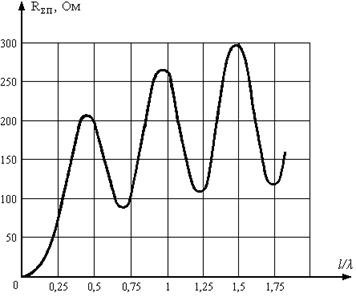
Fig. 35. Rezistența radiației unui vibrator simetric subțire, referitor la un curent la antinod, în funcție de.
După cum se vede din figură, creșterea raportului la începutul rezistenței la radiații a crește vibrator. Acest lucru se explică prin faptul că în timp ce există mai puțin. curent pe întreaga lungime a vibratorului este în fază (adică are aceeași direcție de-a lungul firului) și cu creșterea lungimii firului precum și în cazul dipolului electric de putere de radiație și rezistență la radiațiile elementare crește în consecință. Când lungimea vibratorului devine mai mare decât. porțiuni apar pe un agitator cu un curent de fază opusă, că, la același curent în ventru reduce puterea și rezistența la radiații. Deci, puteți explica cursul curbei în interior. Cu o creștere suplimentară a curbei raport are un caracter oscilatoriu cu valori maxime ale unui număr chiar și minim pentru un număr impar de jumătăți de valuri care se potrivesc lungimea vibratorului.
Este necesar să se ia în considerare două valori ale rezistenței la radiații: Om pentru un vibrator subțire sub formă de undă și Om pentru un val.
În plus față de rezistența la radiații a unui vibrator simetric, rezistența la intrare
Se poate determina componenta activă a rezistenței de intrare
Se poate determina valoarea componentei reactive a impedanței de intrare a unui vibrator simetric
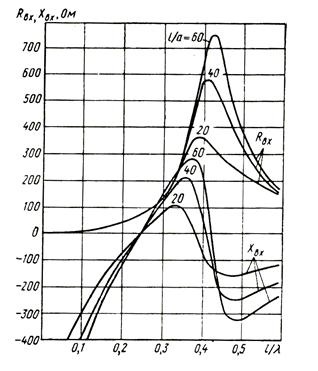
Fig. 36. Curbele componentelor active și reactive ale rezistenței la intrare a vibratoarelor subțiri, în funcție de.
După cum arată o teorie riguroasă și un experiment, un vibrator subțire a cărui lungime totală este exact jumătate din lungimea de undă,
și anume rezistența la intrare. cu excepția activului, are o componentă inductivă. Pe măsură ce grosimea vibratorului crește în lungime, această componentă reactivă scade în mărime, în timp ce componenta activă se modifică nesemnificativ.
Analiza acestor grafice arată că:
1) Cu o variație în interiorul impedanței de intrare, există două regiuni de rezonanță.
Cu - rezonanță consecutivă
La - rezonanță paralelă
Când - are un caracter negativ.
Când conductorul se îngroașește (crește), valoarea rezonanței scade, în special pentru rezonanța paralelă.
2) Cu cât vibratorul este mai gros, cu atât mai slabă este dependența de frecvență a rezistenței de intrare a vibratorului, adică Banda de frecvență se extinde, factorul de calitate scade.