În utilizarea practică a unei anumite măsurători, este important să se evalueze acuratețea acestora. Termenul „precizie“, adică. E. Gradul de aproximare a rezultatelor de măsurare la o anumită valoare reală nu are definiții riguroase și utilizate pentru măsurarea operațiunilor de comparare calitativă. Pentru a cuantifica se aplică conceptul de „eroare de măsurare“ (mai mici de eroare, mai precis).
Eroarea este abaterea rezultatului măsurării de la valoarea reală (adevărată) a valorii măsurate. Trebuie avut în vedere faptul că valoarea reală a cantității fizice este considerată necunoscută și este utilizată în studiile teoretice. Valoarea reală a cantității fizice este stabilită experimental, presupunând că rezultatul experimentului (măsurare) abordează valoarea maximă la valoarea reală. Evaluarea erorii de măsurare este una dintre măsurile importante pentru a asigura o măsurare uniformă.
Erori de măsurare sunt de obicei date în documentația tehnică pentru instrumentele de măsură sau în documentele de reglementare. Cu toate acestea, atunci când consideră că eroarea depinde și de condițiile în care a realizat măsurarea în sine, de la metodologiile de eroare experimentale și caracteristicile subiective ale unei persoane, în cazul în care acesta este direct implicat în măsurători, putem vorbi despre mai multe componente de erori de măsurare, fie pe eroarea totală .
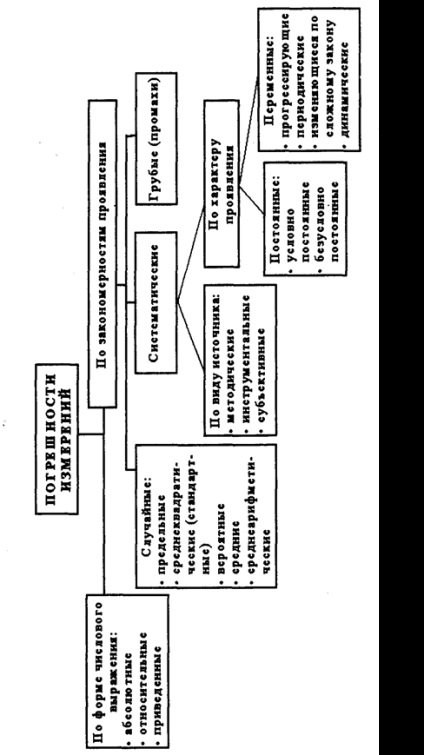
Numărul de factori care afectează precizia măsurătorii este suficient de mare, erorile de clasificare și de măsurare (Figura 2) într-o anumită măsură arbitrară, deoarece diferite erori în funcție de condițiile de măsurare ale procesului sunt prezentate în grupuri diferite.
2.2 Tipuri de erori
Eroarea de măsurare reprezintă abaterea rezultatului măsurătorii X de la valoarea reală Xi a valorii măsurate. La determinarea erorii de măsurare, în locul valorii reale a cantității fizice Xi. utilizați efectiv valoarea sa reală Xd.
În funcție de forma expresiei, se disting erorile de măsurare absolute, relative și reduse.
Eroarea absolută este definită ca diferență # 916; '= X - Hee sau # 916; = X-Xd. și relativă - ca raport # 948; = ± # 916; / Xd # 903; 100%.
Eroarea rezultată # 947; = ± # 916; / # 935; # 925; # 903; 100%, unde # 935; N - valoarea de normalizare a valorii, care este utilizată ca domeniu de măsurare a instrumentului, limita superioară a măsurătorilor etc.
Ca valoare adevărată dată pentru măsurători multiple, media aritmetică:
unde Xi este rezultatul măsurării i, - n este numărul măsurătorilor.
Valoarea. obținută într-o serie de măsurători, este o aproximare aleatorie față de Xi. Pentru a evalua posibilele abateri de la Chi, determinați estimarea deviației standard a mediei aritmetice:
Pentru a estima împrăștierea rezultatelor măsurării individuale Xi în raport cu media aritmetică, deviația medie pătrată a eșantionului este determinată:
Aceste formule sunt utilizate cu condiția ca valoarea măsurată să fie constantă în timpul măsurării.
Aceste formule corespund teoriei limitei centrale a teoriei probabilității, conform căreia media aritmetică a unei serii de măsurători are întotdeauna o eroare mai mică decât eroarea fiecărei măsurători specifice:
Această formulă reflectă legea fundamentală a teoriei erorilor. Din aceasta rezultă că, dacă este necesar pentru a crește acuratețea rezultatului (dacă eroarea sistematică exclusă) de 2 ori, apoi numărul de măsurători trebuie mărită de 4 ori; dacă precizia trebuie să fie mărită cu un factor de 3, numărul măsurătorilor
crește de 9 ori, etc.
Este necesar să se facă o distincție clară între utilizarea cantităților S și # 963; prima este folosită pentru estimarea erorilor rezultatului final, iar cea de-a doua pentru estimarea erorii metodei de măsurare. Eroarea cea mai probabilă a unei singure măsurători În 0,67 S.
În funcție de natura manifestării, cauzele și posibilitățile de eliminare disting între erorile de măsurare sistematice și accidentale, precum și erorile bruște (pierderi).
Eroarea sistematică rămâne constantă sau se schimbă în mod regulat cu măsurători repetate ale aceluiași parametru.
Eroarea aleatorie variază în aceleași condiții de măsurare în mod aleatoriu.
Erori grosiere (erori) apar datorită acțiunilor eronate ale operatorului, funcționării defectuoase a instrumentelor de măsurare sau schimbărilor abrupte în condițiile de măsurare. De regulă, erorile brute sunt detectate ca urmare a prelucrării rezultatelor măsurătorilor utilizând criterii speciale.
Componentele aleatoare și sistematice ale erorilor de măsurare se manifestă simultan, astfel încât eroarea lor totală să fie egală cu suma erorilor atunci când acestea sunt independente.
Valoarea unei erori aleatorii este necunoscută în prealabil, rezultă dintr-un număr de factori nedefiniți. Excludeți erorile aleatorii din rezultate, dar efectul acestora poate fi redus prin procesarea rezultatelor măsurătorilor.
Din punct de vedere practic, este foarte important să puteți formula corect cerințele privind acuratețea măsurătorilor. De exemplu, dacă pentru o eroare de fabricație acceptabilă, luați # 916; = 3 # 963; apoi, creșterea cerințelor de acuratețe (de exemplu, până la # 916; = # 963;), menținând în același timp tehnologia de fabricație, creștem probabilitatea căsătoriei.
De regulă, ei cred că pot fi detectate și excluse erorile sistematice. Cu toate acestea, în condiții reale, este imposibil să excludem complet aceste erori. Există întotdeauna unele rămășițe ne-excluse care trebuie luate în considerare pentru a le evalua limitele. Aceasta este eroarea de măsurare sistematică.
Cu alte cuvinte, în principiu, eroarea sistematică este de asemenea aleatoare, iar această divizare se datorează numai tradițiilor stabilite de prelucrare și prezentare a rezultatelor măsurătorilor.
Spre deosebire de eroarea aleatorie descoperită în general, indiferent de sursele sale, eroarea sistematică este considerată de componentele sale în funcție de sursele de origine. Distingem componentele subiective, metodice și instrumentale ale erorilor.
Componenta subiectivă a erorii este legată de caracteristicile individuale ale operatorului. De regulă, această eroare apare din cauza erorilor în numărarea citirilor (aproximativ 0,1 diviziuni) și a abilităților incorecte ale operatorului. Practic, aceeași eroare sistematică apare din cauza componentelor metodologice și instrumentale.
Articolele componente de eroare datorită metodei de măsurare imperfecțiune, metode care utilizează mijloace de măsurare, formule de calcul incorecte și rezultatele rotunjirii.
Componenta instrumentală rezultă din eroarea intrinsecă a mijloacelor de măsură determinate de clasa de precizie, influența instrumentelor de măsurare asupra rezultatelor și rezoluția limitată a instrumentelor de măsurare.
Scopul de a împărți eroarea sistematică în componente metodice și instrumentale este explicat prin următoarele:
- pentru a spori acuratețea măsurătorilor, este posibil să se identifice factorii limitativi și, prin urmare, să se decidă dacă se îmbunătățește tehnica sau se aleg mijloace mai precise de măsurare;
- devine posibil să se determine componenta de eroare totală care crește cu timpul sau sub influența factorilor externi, și, prin urmare, efectuarea în mod intenționat verificarea periodică și certificare;
- componenta instrumentală poate fi evaluată înainte de elaborarea metodologiei, iar posibilele capacități de precizie ale metodei alese vor fi determinate numai de componenta metodologică.
2.3 Indicatori de calitate a măsurătorilor
Unitatea măsurătorilor, cu toate acestea, nu poate fi asigurată doar prin coincidența erorilor. La măsurare, este de asemenea important să cunoaștem indicatorii de calitate a măsurătorilor. Calitatea măsurătorilor este înțeleasă ca un set de proprietăți care determină obținerea rezultatelor cu caracteristicile de precizie necesare, în forma necesară și în timp util.
Calitatea măsurătorilor este caracterizată de indicatori precum precizia, corectitudinea și fiabilitatea. Acești indicatori ar trebui să fie determinați de estimările la care sunt necesare cerințele de consecvență, imparțialitate și eficiență.
Valoarea reală a valorii măsurate diferă de media aritmetică a rezultatelor observațiilor prin cantitatea de eroare sistematică # C16; care este, X = - # 916; Dacă componenta sistematică este exclusă, atunci X =.
Cu toate acestea, datorită numărului limitat de observații, este imposibilă și determinarea cu precizie a valorii. Se poate estima doar valoarea sa, se indică cu o anumită probabilitate limita intervalului în care se află. O estimare a caracteristicilor numerice ale legii distribuției X, reprezentată de un punct pe axa numerică, se numește punct unu. Spre deosebire de caracteristicile numerice, estimările sunt variabile aleatoare, iar valoarea acestora depinde de numărul de observații n. O evaluare este o estimare care, deoarece n → ∞, reduce probabilitatea la valoarea estimată.
Un obiectiv este o estimare a cărei așteptare matematică este egală cu valoarea estimată.
Eficace se numește o estimare care are cea mai mică variație # 963; 2 = min.
Media aritmetică a rezultatelor observațiilor n satisface cerințele enumerate.
Astfel, rezultatul unei singure măsurători este o variabilă aleatoare. Apoi, precizia măsurării este apropierea rezultatelor măsurătorii de valoarea adevărată a valorii măsurate. Dacă componentele sistematice ale erorii sunt excluse, atunci acuratețea rezultatului măsurătorii este caracterizată de gradul de împrăștiere a valorii sale, adică variația. Așa cum am arătat mai sus, varianța mediei aritmetice # 963; n de mai puțin decât variația unui singur rezultat de observație.
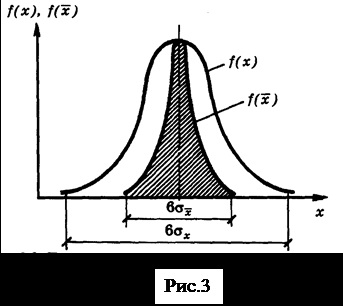
Fiabilitatea măsurătorilor este determinată de gradul de încredere în rezultat și se caracterizează prin probabilitatea ca valoarea adevărată a cantității măsurate să se situeze în vecinătatea indicată a valorii reale. Aceste probabilități sunt denumite confidențiale, iar granițele (cartierele) sunt limite de încredere. Cu alte cuvinte, fiabilitatea măsurării este apropierea de zero a erorii sistematice ne-excluse.
Intervalul de încredere cu limite (sau limite de încredere) de la - # 916; d până la + Q este intervalul de valori ale erorii aleatorii, care cu o probabilitate dată de încredere Pd. acoperă adevărata valoare a cantității măsurate.
pg<- Δд ≤,Х ≤ + Δд>.
Cu un număr mic de măsurători (n 20) și utilizând legea normală, nu este posibil să se determine intervalul de încredere, deoarece legea normală de distribuție descrie comportamentul erorii aleatorii în principiu pentru un număr infinit de mărimi de măsurători.
Prin urmare, pentru un număr mic de măsurători, utilizați distribuția sau t-distribuția studenților (propusă de statisticianul englez Gosset, publicată sub pseudonimul "student"), care oferă posibilitatea stabilirii unor intervale de încredere pentru un număr limitat de măsurători. Limitele intervalului de încredere sunt determinate de formula:
unde t este coeficientul distribuției Studentului, în funcție de probabilitatea de încredere dată Pd și numărul de măsurători n.
Cu un număr tot mai mare de observații, distribuția Studentului se apropie rapid de normal și coincide cu ea deja la n ≥30.
Trebuie remarcat faptul că rezultatele măsurătorilor care nu au o fiabilitate, adică un grad de încredere în corectitudinea lor, nu sunt de valoare. De exemplu, un senzor al unui circuit de măsurare poate avea caracteristici metrologice foarte ridicate, însă influența erorilor de la instalare, condițiile externe, metodele de înregistrare și prelucrare a semnalelor va duce la o eroare de măsurare finită mare.
Alături de indicatori precum precizia, fiabilitatea și precizia, calitatea operațiunilor de măsurare este, de asemenea, caracterizată de convergența și reproductibilitatea rezultatelor. Acești indicatori sunt cei mai obișnuiți atunci când evaluează calitatea testelor și caracterizează acuratețea acestora.
Este evident că două teste ale aceluiași obiect prin aceeași metodă nu dau rezultate identice. O măsură obiectivă a acestora poate servi drept estimări valide din punct de vedere statistic a apropierii așteptate a rezultatelor a două sau mai multe teste obținute cu respectarea strictă a metodologiei lor. Conformitatea și reproductibilitatea sunt considerate ca fiind evaluări statistice ale consecvenței rezultatelor testelor.
Convergența este apropierea de rezultatele a două teste, obținute printr-o metodă, pe instalații identice, într-un laborator. Reproductibilitatea diferă de convergență prin aceea că ambele rezultate trebuie obținute în laboratoare diferite.
3. OBȚINEREA ȘI REPREZENTAREA REZULTATELOR MĂSURĂRII
3.1 Declarația experimentului de măsurare
Atunci când se realizează un experiment de măsurare, este necesar să se determine, în primul rând, ce măsurători (simple sau multiple) trebuie efectuate pentru a determina valoarea cantității fizice măsurate. Următoarea abordare este comună aici:
Dacă eroarea sistematică este eroarea determinantă, adică valoarea sa este mult mai mare decât valoarea erorii aleatorii, atunci este recomandabil să se utilizeze măsurători unice pentru a obține valoarea cantității măsurate;
Dacă eroarea aleatorie este eroarea determinantă, trebuie utilizate mai multe măsurători.
Trebuie să se țină seama de faptul că eroarea sistematică determină deplasarea rezultatelor măsurătorilor și este cea mai periculoasă atunci când nu este suspectată de existență. Detecția unei erori sistematice de măsurare este una dintre cele mai dificile sarcini ale metrologiei. Într-o formă sau alta, trebuie întotdeauna să se decidă atunci când se pregătesc pentru măsurători.