Capitolul 2. Ciclurile Hamiltonian
§ 1. Concepte și definiții de bază
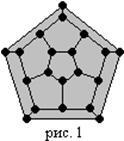
Dacă graficul are un ciclu simplu care conține o singură dată toate vârfurile graficului, atunci un astfel de ciclu este numit ciclu Hamiltonian, iar graficul este denumit graf Hamiltonian. Un grafic care conține o cale simplă care trece prin fiecare vârf se numește semi-hamiltoniană. Această definiție poate fi extinsă la grafice orientate dacă traseul este considerat orientat.
Ciclul Hamiltonian nu conține neapărat toate marginile graficului. Este clar că numai un grafic conectat poate fi Hamiltonian și că fiecare grafic Hamiltonian este semi-Hamiltonian. Observăm că ciclul Hamiltonian nu există în fiecare grafic.
Orice grafic G poate fi transformat într-un grafic Hamiltonian prin adăugarea unui număr suficient de vârfuri. Pentru aceasta, de exemplu, este suficient să adăugăm la nodurile v1, ..., vp ale graficului G nodurile u1, ..., sus și setul de muchii.
Gradul vârfului v este numărul de margini d (v) care au fost incadrați în el, iar bucla este numărată de două ori. În cazul unui grafic orientat, se disting gradul de do (v) deasupra arcurilor de ieșire și di (v) de către arcele primite.
§ 2. Condiții pentru existența ciclului Hamiltonian
Spre deosebire de graficele Euler, în cazul în care există un criteriu pentru a fi graficul Euler, nu există un astfel de criteriu pentru graficele hamiltoniene. Mai mult, problema verificării existenței ciclului Hamiltonian se dovedește a fi NP-completă. Cele mai multe fapte cunoscute au forma: "dacă graficul G are un număr suficient de margini, atunci graficul este Hamiltonian". Oferim mai multe astfel de teoreme.
Teoria lui Dirac. Dacă graficul G (V, E) c n noduri (n ≥ 3) satisface condiția d (v) ≥ n / 2 pentru orice v V, atunci graful G este hamiltonian.
Din contrariul. Fie G să nu fie Hamiltonian. Adăugați la G numărul minim de noduri noi u1, ..., un, conectându-le la toate nodurile lui G astfel încât G: = G + u1 + ... + un este Hamiltonian.
Fie v, u1, w, ..., v - ciclu hamiltonian într-un grafic G 'și v G, u1 G', u1 G. O astfel de pereche de vârfuri v și u1 în ciclul hamiltonian există, pentru că altfel graficul G ar fi Hamiltonian. Apoi w w, w, altfel nu ar fi nevoie de vertex u1. Mai mult decât atât, neadiacenți vârf v cu w vertex, altfel u1 vertex nu a fost necesară.
Mai mult, în cazul în care într-un ciclu de v, u1, w, ..., u 'w', ..., v este un w nod 'adiacent vertex w, atunci vertex v' non-adiacent vertex v, deoarece altfel am putea construi un ciclu hamiltonian v, v '..., w, w', ..., v fără blaturi u1, luând o secvență de noduri w, ..., v „în ordine inversă. Rezultă că numărul de noduri ale grafului G“, care nu este adiacent v, nu este mai mic decât numărul de noduri adiacente w. Cu toate acestea, pentru orice nod w graf G d (w) ≥ p / 2 + n de construcție, inclusiv d (v) ≥ p / 2 + n. Numărul total de noduri (de adiacente și non-adiacente v) este n + p-1. Astfel, avem:
n + p-1 = d (v) + d (V) ≥ d (w) + d (v) ≥ p / 2 + n + p / 2 + n = 2n + p.
Prin urmare, 0 ≥ n + 1, care contrazice faptul că n> 0.
Teorema Orelor. Dacă numărul de vârfuri ale graficului G (V, E) n ≥ 3 și pentru oricare dintre cele două noduri neadiacente u și v se menține inegalitatea:
d (u) + d (v) ≥ n și (u, v) E, atunci graficul G este Hamiltonian.
Graficul G are ciclul Hamiltonian, dacă se află una dintre următoarele condiții:
Condiția Pose: d (vk) ≥ k + 1 pentru k Condiția Bondi: din d (vi) ≤ i și d (vk) ≤ k => d (vi) + d (vk) ≥n (k ≠ i) Condiția este sufixată: de la d (vk) ≤ k ≤ n / 2 => d (vn-k) ≥ n-k. Mai mult, se știe că aproape toate graficele sunt Hamiltonian, adică, unde H (p) este setul de grafice hamiltoniene cu noduri p, iar G (p) este setul tuturor grafurilor cu noduri p. Astfel, problema găsirii unui ciclu hamiltonian, sau echivalent cu problema comis-voiajorului sunt practic cererea, dar nu se știe (și cel mai probabil nu există) algoritm eficient de rezolvare. Un exemplu de grafic atunci când condiția teoremei Dirac nu are loc, dar graficul este Hamiltonian. N = 8; d (vi) = 3; 3 ≥ 8/2 = 4 nu este un grafic Hamiltonian, dar există un ciclu hamiltonian: M = (1, 2, 3, 4, 5, 6, 7, 8, 1) §3. Problemele asociate cu căutarea ciclurilor Hamiltonian Într-o serie de industrii, urmărește următoarea sarcină de planificare. Este necesar să se producă n produse utilizând un singur tip de echipament. Dispozitivul trebuie reconfigurat după ce produsul pi a fost produs (dar înainte de producerea produsului pj), în funcție de combinație (pi, pj). Costul reconfigurării echipamentului este constant și nu depinde de produsele produse. Să presupunem că aceste produse sunt produse într-un ciclu continuu, astfel încât după producerea ultimului produs n, producția primului produs este reluată din nou în același ciclu fix. Se pune întrebarea dacă se poate găsi o secvență ciclică de producție a produselor pi (i = 1,2, ..., n), care nu necesită reconfigurarea echipamentului. Dacă reprezentăm această problemă sub forma unui grafic orientat, atunci răspunsul la întrebarea pusă depinde dacă acest grafic orientat al ciclurilor Hamiltonian are un ciclu sau nu. Dacă nu există secvență de produse ciclice care nu necesită reconfigurare hardware, atunci ce ar trebui să fie secvența de producție cu cel mai mic cost de reconfigurare, adică Solicitarea celui mai mic număr de migrații necesare? Astfel, considerăm următoarele două probleme. Problema 1. Având în vedere un grafic G orientat, este necesar să se găsească un ciclu (sau toate ciclurile) în G al sistemelor hamiltonian dacă există cel puțin un astfel de ciclu. Problema 2. Oferim un ciclu complet orientat G ale cărui arce sunt atribuite greutăți arbitrare C = [cij], găsind un ciclu Hamiltonian care are greutatea cea mai mică. Trebuie notat că dacă graficul orientat G nu este complet, atunci el poate fi privit ca un grafic complet orientat, atribuind arcurilor infinite o greutate infinită.Articole similare