Lăsați un arc atunci când numărul de legături rupte crește linia pe termen nelimitat, iar majoritatea lungimii cartezian AB este dată curba plană a cărei y = f (x), unde x și £ £ b ecuație.
Sub lungimea arcului AB înțeles limita la care tinde lungimea liniei rupte înscrisă în această legătură tinde la zero. Să arătăm că dacă funcția y = f (x) și derivatul său y ¢ = f ¢ (x) sunt continue în intervalul [a. b], atunci curba AB are o lungime egală cu
sau într-o înregistrare redusă
Dacă ecuația curbei AB este dată în forma parametrică
unde x (t) și y (t) sunt funcții continue cu derivate continue și x (a) = a, x (b) = b. atunci lungimea l a curbei AB se găsește din formula
Un exemplu. Găsiți lungimea unui cerc de rază R.
Gasim o parte a lungimii sale din punctul (0; R) pana la punctul (R; 0) (vezi Figura 13). Deci, cum.
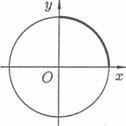
Prin urmare, l = 2 pR. Dacă ecuația cercului este scrisă în forma parametrică x = R cos t. y = R sin t (0 £ t £ 2p), atunci
Fie curba AB dată de ecuația în coordonate polare r = r (j), a £ j b. Să presupunem că r (j) și r '(j) sunt continuu pe intervalul [a. b].
Dacă în egalități x = r cos j, y = r sin j. conectând coordonatele polare și cartesiene, parametrul este unghiul j. atunci curba AB poate fi specificată parametric
Aplicând formula (15), obținem.
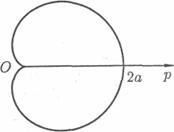
Exemplu Găsiți lungimea cardioidului r = a (1 + cos j).
Cardioidul r = a (1 + cos j) are forma prezentată în figura 14. Este simetrică în raport cu axa polară. Să găsim jumătate din lungimea cardioidului: