Când feromagnetul este magnetizat de un câmp de curent alternativ, dependența are forma unei buclă de histereză (figura 1). Zona buclă este determinată de amplitudinea intensității câmpului magnetic Hmax. Zona va fi cea mai mare atunci când Hmax = Hs. unde Hs este intensitatea câmpului la care proba este magnetizată până la saturație. Această bucla de limitare din Figura 1 este prezentată printr-o linie solidă. La o amplitudine mai mică (Hmax Vârfurile buclei limită și ciclurile parțiale se află pe curba principală de magnetizare. Determinând coordonatele acestor vârfuri, putem construi curba principală de magnetizare și calculam mr (H), așa cum este descris în lucrarea nr. 8. Figura 1 Bucla de histereză Următoarele caracteristici ale feromagnetului sunt determinate din graficul bucla de histerezis limită: - Hs și Bs - parametrii punctului de saturație magnetică; Br este inducția magnetică reziduală; - Hc este valoarea forței coercitive; - w este energia folosită pentru inversarea magnetizării pe unitatea de volum a feromagnetului. Inversarea magnetizării unui feromagnet este legată de consumul de energie, care în cele din urmă se transformă în cea internă. Această energie petrecută pe inversarea magnetizării unui volum unitar al unui magnet, poate fi găsită ca zona delimitată de buclă de histerezis. Astfel, prin utilizarea bucla histerezis pentru proba se poate construi o curbă de magnetizare de bază, un grafic al permeabilității magnetice a câmpului magnetic și de a determina parametrii feromagnet Hc, Br, Hs, Bs și energiei specifice w inversare sale magnetizare. Lipsa histerezisului în această lucrare este observată pe ecranul osciloscopului. Dacă placa baleiere orizontală osciloscop (log X) pentru a da un semnal care variază în funcție de timp, în mod proporțional cu magnetic H. intensitatea câmpului și pe placa verticală (intrare Y) - un semnal care este proporțional cu magnetic de inducție B. fascicul pe ecranul osciloscopului va descrie o buclă de histerezis. Proba de testare a materialului ferimagnetic este sub forma unui miez toroidal două înfășurări (Figura 2): primar (magnetizare) numărul de spire N1 și secundar (N2), concepute pentru a măsura B.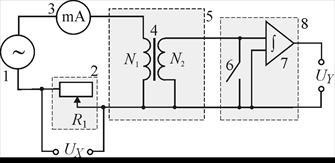
Figura 2. Schema de conexiuni:
1 - un generator de semnal dintr-un formular special; 2 - mini-bloc "Rheostat" cu rezistență R1; 3 - multimetru (modul A 20 mA, intrări COM, mA); 4 - toroid cu înfășurări primare N1 și secundare N2; 5 - mini-bloc "Fer-romagnet"; 6 - cheia amortizorului; 7 - integrator curent; 8 - mini-bloc "Integrator de curent"; UX este tensiunea aplicată la intrarea X a osciloscopului, UX = UR
H; UY este tensiunea aplicată la intrarea Y a osciloscopului, UY = Uint
Măsurarea intensității câmpului magnetic H
Intensitatea câmpului magnetic H din probă atunci când curentul I curge în înfășurarea primară poate fi calculat din formula
unde N1 este numărul de curbe ale înfășurării primare; l este lungimea liniei mediane a toroidului.
La intrarea X a osciloscopului, se aplică o scădere de tensiune la rezistența R1 (vezi figura 2), proporțională cu curentul I în înfășurarea primară a toroidului. În consecință, intensitatea câmpului magnetic din eșantion este proporțională cu deformarea razei x de-a lungul axei X:
unde n este coeficientul de proporționalitate.
Valoarea n poate fi găsită prin măsurarea valorilor x pentru cunoscut H. In acest scop, deplasarea maximă a fasciculului (în mm) la vârful buclei histerezis, care corespunde intensității amplitudinii și valoarea de vârf a curentului în înfășurarea primară
unde I este valoarea efectivă a curentului măsurată prin multimetru.
Înlocuind valorile amplitudinii din (2) și (3), obținem
Măsurarea inducției câmpului magnetic B într-un feromagnet
Atunci când câmpul magnetic creat de înfășurarea primară se modifică, impulsul de inducție (magnitudinea sa este proporțională cu rata de schimbare a fluxului magnetic) și curentul de inducție are loc în secundar:
unde R2 este rezistența circuitului secundar; Ф = BS - flux magnetic printr-o singură rotație a toroidului; B - inducerea câmpului magnetic în toroid; N2 - numărul de rotații ale înfășurării secundare; S este aria secțiunii transversale a miezului.
Ca rezultat al curgerii curentului de inducție în circuitul înfășurării secundare (vezi figura 2), integratorul acumulează o sarcină
Tensiunea Uy. ieșirea de la integrator la intrarea Y a osciloscopului va fi proporțională cu inducerea câmpului magnetic:
unde g este constanta de clasificare a integratorului.
Această tensiune duce la o abatere a y (în mm) a fasciculului de-a lungul verticalei:
unde K este prețul de divizare al axei Y; valoarea K depinde de poziția butonului "Amplificare" al potențiometrului amplificator osciloscop Y; ldel este lungimea divizării mari a axei Y a osciloscopului, mm.
Relațiile liniare (7) și (8) conduc la proporționalitatea lui B (t)
y. care pot fi reprezentate în formă
unde m este un coeficient în funcție de parametrii instalației,
O estimare a energiei specifice w a inversării magnetizării eșantionului:
Folosind formulele (3) și (9), reprezentăm expresia (1) în formă
unde este aria bucla histerezis, exprimată în mm 2. Deoarece x și y sunt reprezentate de numărul de diviziuni mici ale scalei corespunzătoare.
Schema electrică este prezentată în figura 3
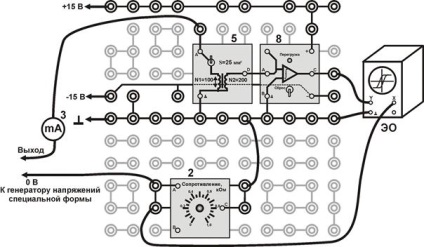
Figura 3 Schema de conexiuni:
EO este un osciloscop electronic; 2, 3, 5, 8 - a se vedea figura 2
Înfășurările primare N1 și secundare N2 sunt înfășurate pe un inel inelar care este realizat din materialul feromagnetic care este studiat. Înfășurarea primară prin care fluxurile de curent alternativ sunt utilizate pentru magnetizarea magnetului și, din parametrii săi, determină intensitatea H atunci când scala X a osciloscopului este calibrată. Pentru a măsura valorile instantanee ale câmpului magnetic alternativ H, semnalul de la reostatul R1 este aplicat la intrarea osciloscopului X.
Înfășurarea secundară este concepută pentru a măsura valorile instantanee ale inducției B a câmpului magnetic în miez. În acest scop, intrarea de tensiune a integratorului este aplicată la intrarea Y a osciloscopului.
Modul de generare a semnalelor formei speciale este un semnal sinusoidal (indicatorul luminos de formă).
Ordinea de executare a muncii
1 Asamblați circuitul electric conform schemei electrice din figura 3.
2 Apăsați butonul "Network" pentru a activa generatorul de tensiune și blocul multimetru. Clapeta 7 a integratorului curent este setată la poziția "Resetare". Apăsați butonul "Setare inițială" (elementul 19, vezi figura 1 la pagina 6) Indicatorul 6 (elementul 19, vezi figura 1 la pagina 6) a formei de undă sinusoidale se va aprinde. Frecvența semnalului de ieșire este setată la 500Hz (vezi indicatorul - poz. 5, figura 1, pagina 6).
3 Activați osciloscopul și scoateți fasciculul de electroni în centrul ecranului.
4 Creșterea curentului I în înfășurarea primară prin setarea butoanelor de nivel de ieșire „0 - 15“ (. Key 10, a se vedea figura 1 de la pagina 6 ..) a generatorului de semnal de formă specială, se obține limita imagine a buclei histerezis, care nu crește în rezultatele curente pentru a mări zona bucla. Astfel, schimbarea rezistența reostatul în „reostatul“ mini-bloc și prin rotirea butonului osciloscop „Îmbunătățirea Y», setați dimensiunea cea mai mare a buclelor, care se potrivesc în ecranul osciloscopului.
5 Selectați valoarea curentului I. la care coordonatele vârfului buzei de histerezis xmax sunt egale cu lungimea axei X a ecranului. Scrieți valorile lui I și xmax în Tabelul 1.
6 În tabelul 1, introduceți parametrii de instalare și de încercare:
N1 și N2 - numărul de rotații ale înfășurărilor primare și secundare;
l este lungimea liniei centrale a miezului;
S este aria secțiunii transversale a miezului;
R2 este rezistența circuitului secundar;
g - constanta de clasificare a integratorului (23,7 × 10 -8 celule / V);
K este prețul divizării axei Y a osciloscopului (a se vedea "Amplificatorul Y." Numărul K este indicat în V / div-volți pentru o diviziune mare a axei Y);
- lungimea divizării mari a axei osciloscopului Y (în mm) - este măsurată de o riglă.
Măsurarea parametrilor circuitului de histereză magnetică
1 Trageți oscilograma bucla de histereză limită pe hârtia de urmărire.
2 Măsurați coordonatele pozitive și negative ale punctelor de buclă care corespund valorilor forței coercitive Hc. reziduale de inducție Br. intensitatea de saturație Hs și inducția de saturație Bs (a se vedea figura 1). Înregistrați rezultatele acestor măsurători în Tabelul 2.
Calculați rezultatele calculelor din tabelul 2.
3 Pe oscilograma buclă de histereză, estimați aria sa în mm 2 (în funcție de numărul de celule de hârtie milimetrică prinse în interiorul bucla).
Determinați prin formula (11) energia specifică w a inversării magnetizării feromagnetului:
Estimați energia folosită pentru remagnetizarea unei mostre de volum V într-un singur ciclu ca:
Înregistrați rezultatele în tabelul 2.
4 Din datele din Tabelul 3 pentru fiecare pereche de valori ale lui x și y, se calculează valorile H și B din formulele (3) și (9) și se calculează permeabilitatea magnetică mr. Din expresia: B = m0mr H:
unde valoarea m0 = 4p × 10 -7 HN / m.
Calculați rezultatele calculelor din tabelul 3.
5 Pe baza datelor din Tabelul 3, se compune curba principală de magnetizare și graficul dependenței.
6 În încheierea lucrării, se reflectă trăsăturile formei curbelor experimentale:
7 Comparați cursul curbei principale de magnetizare cu poziția maximului pe grafic;
b) compara curbele obtinute cu dependente teoretice si experimentale cunoscute.
Faceți o concluzie cu privire la materialul de bază: magnetic moale sau rigid magnetic, - compararea valorii găsite a Br cu Bs.
1 Afișați curba principală de magnetizare și dependența de feromagneți pe grafic:
2 Care este diferența dintre curba principală de magnetizare și buclă de histerezis?
3 Care sunt proprietățile caracteristice ale feromagnetilor și caracteristicile magnetizării lor.
4 Descrieți modificările în structura domeniului unui feromagnet în timpul magnetizării sale (creșterea intensității câmpului H).
5 Din ce cantități depinde:
a) intensitatea H a câmpului magnetic al toroidului;
b) inducția magnetică B a unui toroid cu miez feromagnetic;
c) permeabilitatea magnetică r a materialului de bază al toroidului?
6 Ce formule (din cele prezentate în lucrare) arată dependența cantităților B și H de alte cantități?
7 Ce valori măsurate și ce formule sunt utilizate pentru a determina următoarele valori:
a) intensitatea câmpului magnetic H în miez;
b) inducția magnetică B;
c) permeabilitatea magnetică mr a materialului de bază?
8 Specificați modul de includere și alocare a următoarelor elemente:
a) rezistența R1 în circuitul primar;
b) integratorul curent în circuitul de înfășurare secundar.
9 Care este valoarea curentă în înfășurarea primară măsurată prin ampermetrul utilizat?
10 Denumiți cantitățile proporționale cu care se schimbă tensiunea Ux și Uy (la intrările X și Y ale osciloscopului).
11 Gasiti punctele caracteristice ale buclei de histerezis, ale caror coordonate sunt folosite:
b) pentru construirea curbei principale de magnetizare?
12 Pe ce formule din lucrare se determină următoarele valori:
a) Inducția reziduală Br; b) forța coercitivă Hc;
c) permeabilitatea magnetică a nucleului mr?