Funcția y = sinx, proprietăți ee și grafic
Funcția y = sin X.
Mai sus, în §20, am formulat o regulă care să permită fiecărui număr t să corespundă cu numărul cos t, adică a caracterizat funcția y = sin t. Observăm câteva din proprietățile sale.
Proprietățile funcției u = sin t.
Proprietate 1. Domeniul definiției este setul K al numerelor reale.
Acest lucru rezultă din faptul că la orice număr 2 corespunde cercului numeric un punct M (1), care are o ordonată bine definită; această ordonată este cos t.
Proprietatea 2. u = sin t este o funcție ciudată.
Acest lucru rezultă din faptul că, așa cum sa dovedit în §19, pentru orice egalitate
Prin urmare, graficul funcției u = sin t, ca grafic al oricărei funcții impare, este simetric în raport cu originea în sistemul de coordonate dreptunghiular tOu.
Proprietatea 3. Funcția u = sin t crește pe interval
Acest lucru rezultă din faptul că, ca punct pentru primul trimestru al circumferinței ordonata numerică crește progresiv (de la 0 la 1 - vezi Figura 115 ..), și ordonata scade treptat (la 1 la 0 ca punct de mișcare al circumferinței numerice doilea trimestru - cm. Fig. 116).
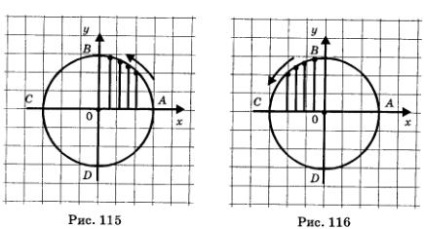
Proprietatea 4. Funcția u = sin t este mărginită de jos și de sus. Acest lucru rezultă din faptul că, așa cum am văzut în §19, pentru orice inegalitate
Proprietatea 5. (Această valoare atinge funcția în orice punct al formularului (această valoare ajunge în orice punct al formularului
Folosind proprietățile obținute, vom construi graficul funcției care ne interesează. Dar (atenție!) În loc de u - sin sin, vom scrie y = păcat x (după toate suntem obișnuiți să scriem y = f (x), și nu u = f (t)). Prin urmare, vom construi, de asemenea, un grafic în sistemul familiar de coordonate xOy (mai degrabă decât tOy).
Noi compunem un tabel de valori ale funcției y = sin x:
Notă. Iată o versiune a originii termenului "sine". În latină, sinusul înseamnă îndoire (șir de arc). Graficul construit într-o oarecare măsură justifică această terminologie.
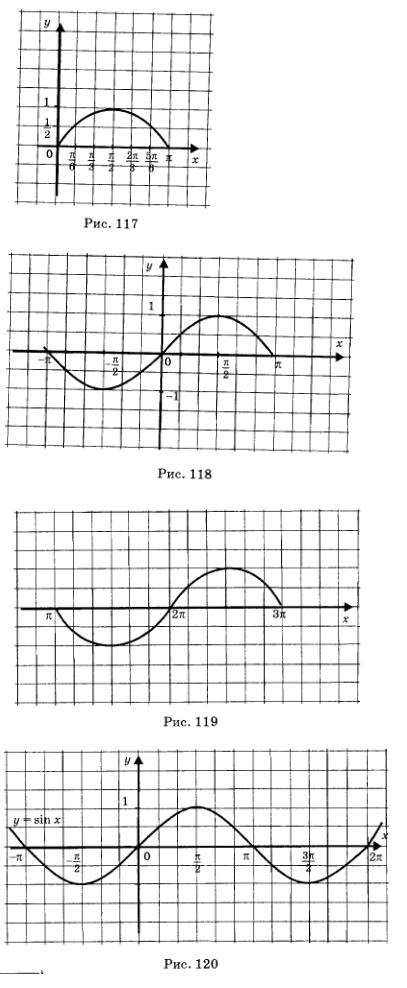
Linia care servește ca grafic al funcției y = sin x se numește sinusoid. Partea sinusoidului descris în Fig. 118 sau 119, se numește un val de sinusoid, iar acea parte a sinusoidului prezentată în Fig. 117, se numește semicuplu sau arc de sinusoid.
AG Mordkovich clasa Algebra 10
Dacă aveți corecții sau sugestii pentru această lecție, scrieți-ne.
Dacă doriți să vedeți alte ajustări și dorințe pentru lecții, consultați aici - Forumul educațional.