Francis Hill "Graphics pentru computerul OpenGL .Coding pentru profesioniști" p.224
Combinări convexe de vectori Combinațiile convexe ocupă un loc important în matematică și în numeroase aplicații grafice. Combinația convexe (combinație convexă) apare ca limitând în continuare combinații de afinitate, nu numai cantitatea de coeficienți de combinație liniară trebuie să fie egale una, dar fiecare coeficient trebuie să fie mai mult decât atât non-negativ. Astfel, combinația liniară a lui (4.3) este convexă dacă
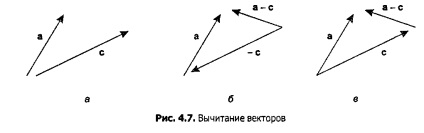
4.2. Prezentare generală a vectorilor
În consecință, toate a<должны находиться между 0 и 1. (Почему?)
Astfel, 0.3a + 0.7b este o combinație convexă a vectorilor a și b, în timp ce 1.8a - 0.8b nu este. Setul de coeficienți ava2. am este uneori numită o partiție de unitate, ceea ce înseamnă că o singură cantitate de "material" este împărțită în părți. Combinările convexe apar deseori în aplicații în care se formează o singură cantitate de "amestec" și se pot combina numai cantități pozitive de diferite ingrediente. Astfel de combinații apar în contextele cele mai neașteptate. De exemplu, vom vedea în capitolul 11 că curbele spline sunt de fapt combinații convexe ale unor vectori, și în studiul nostru de culoare (capitolul 12) aflăm că fiecare luminozitate culoare poate fi reprezentat ca o combinație convexă de trei culori simplu!
Se pare util să folosim noțiunea "setul tuturor combinațiilor convexe" ale unui anumit set de vectori. Pentru doi vectori v4 și v2, mulțimea tuturor combinațiilor convexe este setul tuturor vectorilor formei
unde parametrul a poate varia de la 0 la 1. (De ce?) Ce este acest set? Transformând egalitatea (4.6), obținem:
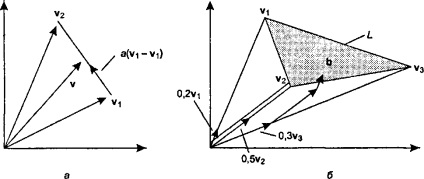
Fig. 4.8. Setul de vectori reprezentabili prin combinații convexe Fig. 4.8, a arată un vector v egal cu suma v, și o parte din \ 2-v. iar capătul vectorului v este situat pe linia dreaptă care leagă v și y2. Deoarece o schimbare 0 - 1, la sfârșitul v pot ocupa poziții care coincid cu toate punctele de un segment de linie care leagă capetele v, și V2, și numai acele dispoziții.