Sub influența forțelor externe, corpul își schimbă forma și volumul, ca rezultat al acesteia, apar forțe interne, încercând să restabilească forma anterioară. Densitatea de suprafață a forței care apare în fiecare element al corpului se numește stres.
voltaj # 963; Este o cantitate vectorială. Aceasta depinde de proprietățile intrinseci ale roca (puterea și caracterul de legături între particule), formează un eșantion și efectul forțelor externe. Forțele care acționează într-o direcție pentru a provoca în eșantion o stare liniară de stres care acționează în două direcții, dar într-un singur plan - a subliniat plat de stat, iar în alte cazuri - starea de stres volumetric.
Într-o rasă absolut densă, tensiunile sunt calculate prin formula:
unde S este zona în care acționează forța.
În roci poroase
unde S0 este zona de contact a boabelor minerale; Sn este zona ocupată de pori.
Stresurile sunt concentrate numai în zona de contact a boabelor minerale
Prin urmare, odată cu creșterea porozității, fisurii și intemperii, toate celelalte condiții fiind egale, stresul în creșterea rocilor. Gradul de creștere a presiunilor reale din piatra poroasă este și mai mare datorită concentrației locale de stres care are loc în colțurile crăpăturilor și porilor.
Luați în considerare un corp de formă arbitrară, care este în echilibru sub acțiunea forțelor externe aplicate. Tăiați corpul considerat mental de orice suprafață în două părți. Înlocuim acțiunea unei părți a forțelor interne aplicate secțiunii transversale, astfel încât partea rămasă să fie în echilibru. În general, forțele interne sunt distribuite neuniform pe suprafața secțiunii transversale. Să ne identificăm o platformă elementară pe care acționează forța.
În acest caz, raportul
se numește vectorul de tensiune la locul respectiv.
Prin disecarea corpului luate în considerare de planuri paralele cu un sistem de coordonate dreptunghiular, se poate ajunge la cubul elementar pe care fiecare față exterioară are propriul vector de stres. Proiecțiile acestor vectori pe axa de coordonate reprezintă nouă componente de stres - două tangente și una normală pe fiecare față a cubului (Figura 10). Toate acestea reprezintă o cantitate fizică, numită tensorul de stres.
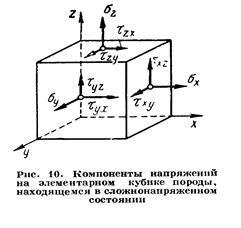
Tensorul de stres are următoarea formă
Suma momentelor în raport cu orice margine a cubului elementar trebuie să fie zero. Aceasta implică legea tangenței tensiunii la forfecare:
Astfel, starea de stres a unui solid în orice plan poate fi caracterizată de eforturile normale și tangențiale care acționează în el. Acestea sunt legate între ele și pot fi calculate prin metoda de adăugare vectorială. Figura 11 prezintă un exemplu de încărcare a eșantionului cu forțe axiale () și laterale () (). Pentru a găsi stresul normal () și tangențial (), care acționează pe o platformă înclinată, situată sub un unghi. se poate utiliza metoda grafică folosind cercul stresului Mohr, care sunt construite după cum urmează: pe axa abscisei reprezintă valorile maxime și minime ale tensiunilor normale care acționează asupra eșantionului; (Figura 11). Pe diferența dintre segmente, ca pe diametru, este construit un semicerc.
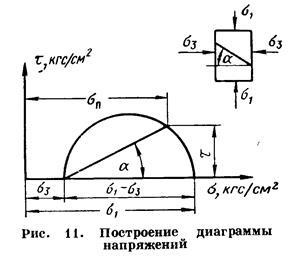
Valorile tangente și normale ale tensiunii în orice punct al eșantionului pot fi determinate dacă este dat unghiul de înclinare al planului în care sunt determinate tensiunile. În acest unghi, din punctul de intersecție al cercului cu abscisa, trasează o linie dreaptă la intersecția cu semicercul. Coordonatele punctului de intersecție al semicercului cu o linie dreaptă sunt numeric egale cu valorile anumitor tensiuni. La fiecare valoare particulară a stării de stres corespunde propriului său cerc de solicitări.
Stresurile din stânci pot apărea sub influența nu numai a forțelor externe, ci și a diferitelor domenii fizice. Voltages sunt termică, contracție, cauzate de volumul de răcire neuniformă, care rezultă rezidual din distribuția tensiunilor inegală datorită unui stres local al materialului și altele. Aceste tensiuni sunt suprapuse de tensiune de la un impact extern, pe care le poate scădea crește sau.
Sub influența forțelor externe, roca suferă modificări în dimensiuni, volum sau formă liniară, care se numesc deformări.
Deformațiile corespunzătoare tensiunilor normale sunt exprimate în termeni de variație relativă a dimensiunilor liniare ale eșantionului
Unde l 'și l - lungimea eșantionului, respectiv, în stare deformată și nedeformată.
Deformările relative care corespund tensiunilor tangențiale sunt exprimate prin tangenta unghiului de forfecare a fețelor volumului elementar al eșantionului. Având în vedere micșorarea unghiului, relația este valabilă.
Deformările de alungire și de forfecare pot fi descompuse în componente de-a lungul axelor de coordonate. În teoria elasticității (o secțiune a teoriei deformațiilor) se deduce tensorul deformărilor. Determinarea stării de deformare în orice punct al corpului: