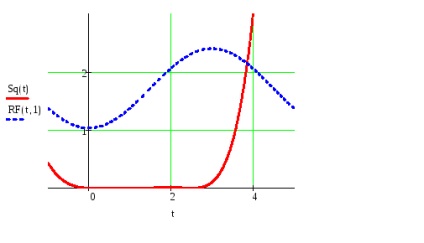
Dat fiind T este o funcție periodică a f (t)
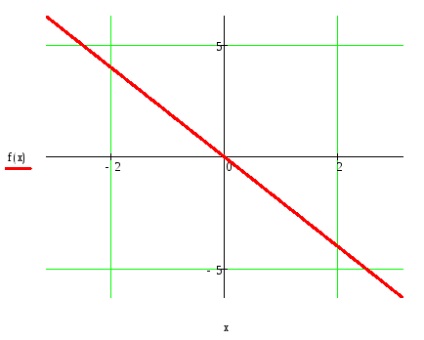
Pentru a justifica posibilitatea extinderii lui f (t) într-o serie Fourier, se stabilește forma convergenței seriei Fourier la f (t).
Teorema lui Dirichlet: Dacă T este o funcție periodică a lui f (t), satisface condițiile Dirichlet pe un interval închis de lungime T:
Este continuă sau are un număr finit de puncte de discontinuitate de primul tip
Monotonul are fie un număr finit de maxime și minime
Seriile Fourier converg de-a lungul axei t și suma seriei Fourier este egală cu f (t) la toate punctele acestei funcții este continuă în punctul t0 de discontinuitate a funcțiilor primului tip f (t) este egală cu suma seriei Fourier a funcției f (t) satisface condițiile de convergență, în medie.
Lyapunov Simptom: Dacă T - funcția periodică f (t) îndeplinește condițiile de continuă și pătrat pe porțiuni integrabile, atunci seria Fourier medie pătratică converg spre f (t).
Construiți un grafic al sumei unei serii Fourier.
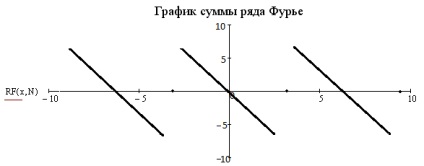
Reprezentați funcția dată cu o serie Fourier trigonometrică în avans:
b) calculați coeficienții seriei Fourier.
Coeficienți ai seriei Fourier
Extinderea trigonometrică a φ-ии într-o serie Fourier
Construiți spectrul de amplitudine și de fază a funcției.
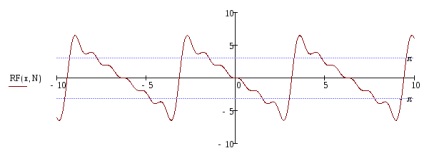
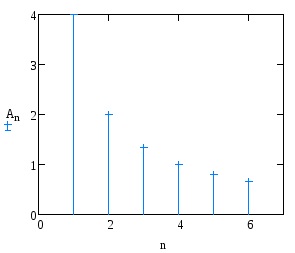
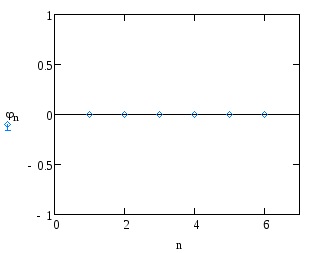
Determinați numărul de armonici ai extinderii funcției într-o serie Fourier care conține în total nu mai puțin de 90% din energie.
Pentru a determina numărul de armonici care conțin în total nu mai puțin de 90% din energie, mai întâi se calculează energia introdusă de fiecare armonică separat în conformitate cu următoarea formulă:
Contribuția armonicilor la energie
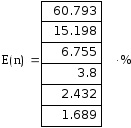
Calculați eroarea între rădăcină și pătrat între funcția originală f (t) și suma parțială Fourier pentru t care aparține intervalului de întreținere.
Formula de calcul pentru eroarea medie-pătrată rădăcină:
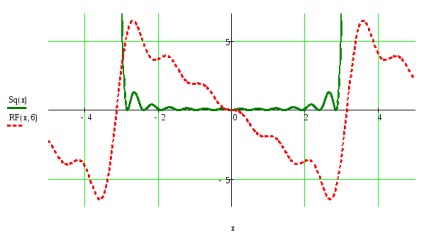
Construiți graficele funcției date și suma parțială a seriei Fourier pentru valorile t care aparțin intervalului sarcinii f (t), luând numărul de armonici definite în clauza # 5.
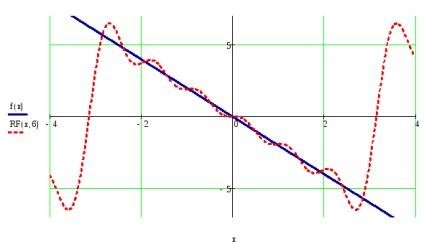
Construiți un grafic al pătratului deviațiilor funcției și suma parțială a seriei pentru t din intervalul sarcinii f (t).
Pentru o funcție definită pe un interval finit, construiți o extensie periodică într-o manieră prescrisă.
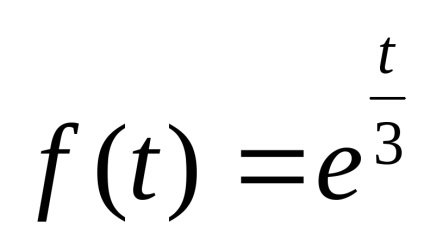
Pentru a justifica posibilitatea extinderii lui f (t) într-o serie Fourier, se stabilește forma convergenței seriei Fourier la f (t).
Această funcție f (t) satisface condițiile din teorema lui Dirichlet:
Teorema lui Dirichlet: Dacă T este o funcție periodică a f (t), satisface condițiile Dirichlet pe un interval închis de lungime T:
Este continuă sau are un număr finit de puncte de discontinuitate de primul tip
Monotonul are fie un număr finit de maxime și minime
Seriile Fourier converg de-a lungul axei t și suma seriei Fourier este egală cu f (t) la toate punctele acestei funcții este continuă în punctul t0 de discontinuitate a funcțiilor primului tip f (t) este egală cu suma seriei Fourier a funcției f (t) satisface condițiile de convergență, în medie.
Teorema lui Weierstrass: dacă T este o funcție periodică a f (x) pe un interval închis. De exemplu [-T / 2, T / 2] îndeplinește condițiile de continuitate și f (-T / 2) = f (T / 2), atunci seria Fourier a trigonometric converg spre f (x) uniform.
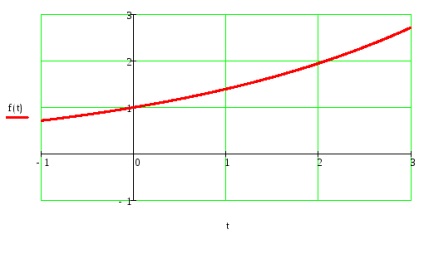
Construiți un grafic al sumei unei serii Fourier.
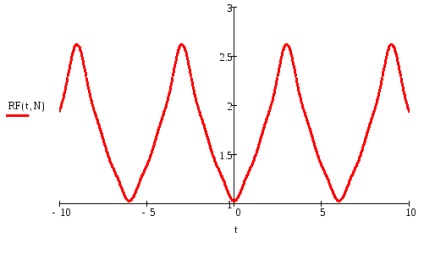
Reprezentați funcția dată cu o serie Fourier trigonometrică în avans:
b) calculați coeficienții seriei Fourier
Coeficienți ai seriei Fourier
Extinderea trigonometrică a φ-ии într-o serie Fourier
Construiți spectrul de amplitudine și de fază a funcției.
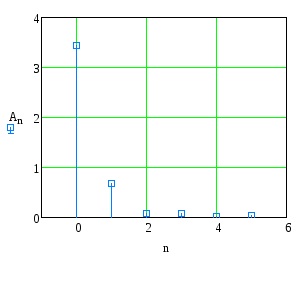
Determinați numărul de armonici ai extinderii funcției într-o serie Fourier care conține în total nu mai puțin de 90% din energie.
Contribuția armonicilor la energie
Calculați eroarea între rădăcină și pătrat între funcția originală f (t) și suma parțială Fourier pentru t care aparține intervalului de întreținere.
Construiți graficele funcției date și suma parțială a seriei Fourier pentru valorile t care aparțin intervalului sarcinii f (t), luând numărul de armonici definite în clauza # 5.
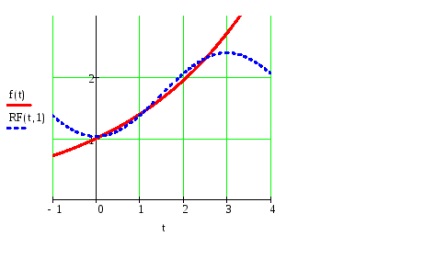
Construiți un grafic al pătratului deviațiilor funcției și suma parțială a seriei pentru t din intervalul sarcinii f (t).