La momentul inițial al mișcării, viteza cilindrului este zero și energia mecanică totală este egală cu energia potențială. Atunci când se deplasează în plan orizontal, energia mecanică totală a cilindrului este egală cu suma energiei cinetice și a energiei potențiale a cilindrului. Prin legea conservării energiei mecanice totale, obținem:
Energia potențială a cilindrului este determinată de poziția centrului de masă al cilindrului deasupra planului orizontal. De aceea :. unde g este accelerația datorată gravitației.
După cum se știe, rularea cilindrului de-a lungul unei suprafețe plane poate fi privită ca o rotație cu viteză unghiulară # 969; în jurul axei de rotație instantanee care trece de-a lungul liniei de contact a suprafeței cilindrice și a planului. În figură, axa de rotație instantanee trece prin punctul M perpendicular pe planul figurii. În consecință, energia cinetică este determinată de expresie
unde I este momentul inerției cilindrului față de axa de rotație instantanee. Din expresia binecunoscută pentru momentul inerției cilindrului în raport cu axa simetriei și teorema lui Steiner, obținem:
Expresia (1) luând în considerare formulele (2) și (3) ia forma
Din ecuația (4) pentru viteza unghiulară # 969; urmează:
Momentul pulsului L, când cilindrul se deplasează la planul orizontal, este îndreptat de-a lungul axei de rotație instantanee, așa cum se arată în figură. Modul de cuplu de impulsuri
răspundă: # 969; = 72 rad / s; L = 2,7 (kg × m²) / s.
12. Două bile, o masă m1 = 2,0 kg, a doua m2 = 3,0 kg, pe un plan de mișcare orizontală în direcții reciproc perpendiculare față și se ciocnesc complet neelastic. Găsiți după coliziune viteza bilelor. direcția de viteză și o parte din energia mecanică a bilelor, care a trecut în energia internă a bilelor. Înainte de coliziune, viteza primei mingi = 5,0 m / s, a doua = 3,0 m / s.
Soluția
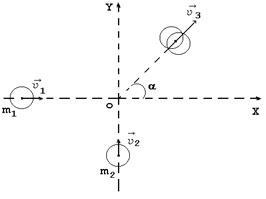
În plan orizontal, introducem sistemul de coordonate XOY. așa cum se arată în Fig. 1. Coliziunea bilelor apare la originea sistemului de coordonate. Coliziunea este absolut inelastică, astfel încât bilele "se îmbină" și se mișcă împreună cu viteza. așa cum se arată în Fig. 1. Forța externă (gravitație) care acționează asupra bilelor este perpendiculară pe planul orizontal și, prin urmare, legea conservării momentului
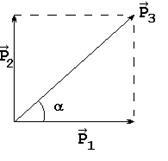
în cazul în care este impulsul primei mingi înainte de coliziune; - impulsul a doua minge înainte de coliziune; - impulsul de bile după coliziune. Din caracterul mișcării bilelor și din legea conservării impulsului rezultă că direcția vectorilor ar trebui să corespundă Fig. 2, iar modulele vectorilor sunt legate de
Din ecuația (2) pentru viteză, obținem:
unghi # 945; caracterizarea direcției de viteză. poate fi găsit din Fig. 2 prin formula:
În cazul unei coliziuni absolut inelastice, energia mecanică a corpurilor scade cu W. care a trecut în energia internă a bilelor. Mișcarea are loc pe plan orizontal, astfel încât energia mecanică a sistemului se datorează energiei cinetice a bilelor. În cele din urmă, pentru cantitate # 916; W urmează
Răspuns: = 2,7 m / s; # 945; = 42º; # 916; W = 20 J.
13. Zhukovskogo bancă se rotește la n1 = 1,0 v / de persoana care deține poziționată orizontal în centrul m metalic tijă de masă = 5,0 kg și lungime l = 1,5 m. Definirea n2 umane viteza de rotație și de locuri de muncă perfectă A Dacă întoarce tija în poziție verticală. Momentul de inerție a omului și a bancnotei I0 = 5,0 kg # 8729; m².
Soluție Rotația unei persoane cu o tijă are loc în jurul unei axe verticale, momentul forțelor externe în raport cu care este zero. Prin urmare, magnitudinea momentului unghiular L față de axa verticală rămâne neschimbată atunci când tija este rotită, adică .. sau (1)
unde I1 și 1 - momentul inerției și viteza unghiulară a unei persoane cu o tijă situată orizontal; I2 și 2 - momentul inerției și viteza unghiulară a unei persoane cu o tijă situată vertical. Viteză unghiulară # 969; și numărul de revoluții pe unitate de timp sunt legate de
Momentul de inerție a tijei Ic în raport cu axa perpendiculară pe tija și trecând prin centrul său de masă. prin urmare
Când tija este transformată într-o poziție verticală, momentul de inerție devine zero. În consecință, (4) În formula (1) se substituie relațiile (2) - (4), obținem :. Prin urmare, pentru valoarea n2 rezultă că:
Lucrarea lui A. completat de o persoană atunci când tija este rotită este egală cu schimbarea energiei cinetice. prin urmare
SARCINI PENTRU SOLUȚII INDEPENDENTE
1,44. Platforma sub forma unui disc se rotește prin inerție în jurul unei axe verticale cu frecvența n1 = 14 min -1. La marginea platformei se află un bărbat. Când persoana sa mutat în centrul platformei, frecvența a crescut la n2 = 25 min -1. Greutatea persoanei m = 70 kg. Determinați masa platformei. Momentul inerțiunii omului este calculat ca pentru un punct material.
1,45. O persoană care cântărește m0 = 60 kg se află pe o platformă fixă cu o masă de m = 100 kg. Cu ce frecvență n se va roti platforma dacă o persoană se mișcă în jurul unui cerc cu o rază de r = 5,0 m în jurul axei de rotație? Viteza de deplasare a unei persoane în raport cu platforma u0 = 4,0 km / h. Radiusul platformei R = 10 m. Citiți platforma ca un disc omogen și persoana ca o masă punctuală.
1.46. Bilele se rostogolește de la un plan înclinat de înălțime h = 90 cm. Ce viteză liniară va avea mingea în momentul în care se aliniază de la planul înclinat? Momentul inerției mingii este J = 0,40 m × R 2.
1.47. Două bile se deplasează unul spre celălalt de-a lungul axei X. Masa primei mingi este m1 = 0,20 kg, masa celei de-a doua mingi este m2 = 0,30 kg. Înainte de coliziunea proiecției vitezelor bilelor pe axă, = 1,0 m / s, = -1,0 m / s. Găsiți proiecțiile vitezelor bilelor și după coliziunea centrală absolută elastică.
(= -1,4 m / s, = 0,60 m / s)
1.48. O bară subțire uniformă de lungime L se poate roti în jurul unei axe orizontale care trece prin capătul tijei perpendiculare pe ea. Tija a fost deviată la 90 ° față de poziția de echilibru și a fost eliberată. Determinați viteza u a capătului inferior al tijei în momentul trecerii echilibrului.
1.49. O bară subțire uniformă, cu lungimea l și masa m, se poate roti liber în jurul unei axe orizontale care trece prin unul din capetele sale. Tija este instalată orizontal și eliberată. Fără a lua în considerare fricțiunea, determinați viteza unghiulară a tijei în momentul în care trece poziția de echilibru. Construiți un grafic al dependenței de accelerația unghiulară a tijei pe unghiul dintre tija și orizont.
1.50. O bilă uniformă continuă să se rostogolească pe un plan înclinat cu lungimea de 5 m. Unghiul de înclinare al planului la orizont este a = 30 °. Determinați viteza mingii la capătul planului înclinat, momentul mișcării mingii pe suprafața orizontală și construiți calitativ dependența energiei cinetice a mingii ca funcție de timp. Pierderea energiei este neglijată. Momentul inerției mingii în raport cu axa care trece prin centrul de masă, J0 = mR2.
(u = 5,9 m / s, t = 1,7 s)
1.51. role solide cilindru pe o suprafață orizontală pentru timpul t = 3,0 c și se oprește după care parcurge o distanță de 9,0 m. Pentru a determina coeficientul de frecare, presupunând că constantă. Construiți calitativ energia cinetică a corpului în funcție de timpul mișcării.
1.52. Un arbore cu masa m = 50 kg și o rază R = 5,0 cm rotit cu o frecvență n = 10 rev / s. Un tampon de frână cu o forță F = 30 N a fost aplicat pe suprafața sa cilindrică și, după 8,0 secunde după începerea frânării, arborele sa oprit. Determinați coeficientul de frecare, presupunând că este constant. Construiți un grafic al vitezei unghiulare și accelerației unghiulare a arborelui ca o funcție a timpului în intervalul de frânare.
1.53. Bilele și discul solid au aceleași mase și se rostogolesc fără alunecare pe o suprafață orizontală cu aceleași viteze constante. Energia cinetică a mingii W1 = 70 J. Determinați energia cinetică a discului W2. Identificați raportul dintre proiecțiile momentului unghiular al corpurilor Lz1 / Lz2 și axa de rotație instantanee, dacă R1 / R2 = 0,7.
1.54. Un corp de masă M este suspendat de șiruri de lungime l. Un glonț cu masă intră în corp și se blochează în el, firul deviază apoi într-un unghi a. Găsiți viteza glonțului. Considerați că întreaga masă a corpului M este concentrată la o distanță l față de punctul de suspendare.
1.55. Cât timp va cilinda cilindrul în jos dintr-un plan înclinat de lungime l = 2,0 m și înălțime h = 0,10 m, dacă presupunem că nu există alunecare? Creșterea calitativă a dependenței Wk cinetic și a potențialului Wp al energiei cilindrului în funcție de timp.
1,56. Două bile de masă m1 = 10 kg și m2 = 15 kg sunt suspendate pe fire de lungime l = 2,0 m, astfel încât bilele să se atingă reciproc. Bilele mai mici au fost deflecte la un unghi de j = 60 ° și au fost eliberate. Determinați înălțimea la care ambele bile vor crește după impact. Strike bilele ca inelastice.
1.57. M1 masa cilindrului = 3,0 kg și raza R = 10 cm, sprijinindu-se pe un plan dor de masa glonț m2 = g 9,0, zboară la o viteză de u0 = 60 m / s. Glonțul zboară paralel cu planul la o înălțime h = 0,12 m de, și perpendicular pe generatoarea cilindrului. Presupunând că impactul este absolut inelastic, găsiți viteza liniară a axului cilindrului, viteza unghiulară a cilindrului. Alunecarea cilindrului este neglijată.
1,58. Corpul cu masele m1 și m2 sunt conectate fir imponderabil și inextensibil, care este transferată prin masa m unitate. instalat pe marginea mesei. Corpul m1 este situat pe suprafața mesei într-o stare fixă. Corpul m2 este liber să stea. La momentul t = 0, corpul m1 a fost eliberat, iar întregul sistem a început să se miște. Presupunând că coeficientul de frecare între masă și m1 corpului egală cu m, neglijând blocul de alunecare și firul pe frecarea în axa blocului, găsi activitatea forțelor de frecare în primele t secunde după începerea mișcării. Blocul este considerat un disc uniform.
1.59. O minge de oțel cu masa m = 8 g, care zboară orizontal la o viteză de 600 m / s, cade într-o bară cu o masă M = 4 m. atașat la perete de un arc cu o rigiditate k = 24 kN / m. Presupunând că traiectoria mingii este perpendiculară pe suprafața barei și coincide cu axa arcului, se determină amploarea comprimării maxime a arcului, dacă tensiunea a fost:
1) absolut inelastică; 2) absolut elastică.
Înregistrați legea schimbării în deformarea arcului ca o funcție a timpului pentru cazurile 1 și 2.
1.60. Un piston montat pe rigiditate arc k = 10 kN / m, după blocajul în acesta orizontal care zboară cu o viteză u = 520 m / s Bullet 20 g deplasată cu x = 8 cm. Se determină greutatea pistonului M. forța dacă frecarea de peretele cilindrului este de 900 N.
1.61. Firul cu încărcătura suspendată pe acesta a fost respins de unghiul a și eliberat. La ce unghi b va filamentul cu sarcina să devieze, dacă în timpul mișcării sale este întârziată de un știft plasat vertical în mijlocul firului? Construiește o dependență calitativă a vitezei încărcăturii la timp, presupunând că pierderea de energie din sistem nu se produce.
1.62. Pucul de hockey, având o viteză inițială u = 5,0 m / s, trece înainte de impactul pe placa de drum S = 10 m. Coeficientul de frecare al șaibei este de aproximativ 0,10 gheață. Având în vedere impactul asupra panoului este absolut elastic și neglijând rezistența aerului, determinați modul în care pucul va merge după impact. Construiește un grafic al dependenței ux = f (x), punând direcția pozitivă a axei OX pe placă.
1.63. O persoană stă pe un cărucior staționar și aruncă orizontal o piatră cu o masă m1 = 2,0 kg cu o viteză u = 8,0 m / s. Determinați ce fel de muncă A face atunci când aruncați o persoană, dacă greutatea căruciorului cu o persoană m2 = 140 kg. Construiți un grafic al dependenței lucrării A = f (m2), dacă m2 este o variabilă.
1.64. Gimnastul "răsucește soarele" pe traversă. Presupunând că întreaga masă m gimnasta sa concentrat în centrul său de masă și de gimnaste viteză la partea superioară egală cu zero, pentru a determina forța care acționează asupra gimnastei mâinilor la punctul cel mai jos. Construiește un grafic al dependenței componentei verticale a vitezei gimnastei de timpul uy = f (t). Pentru începutul numărării, luați poziția superioară a gimnastei. Fricțiunea este neglijată.