Funcția - dependența variabilei y de variabila x, pentru care fiecare valoare a variabilei x corespunde unei singure valori a variabilei y.
O variabilă x se numește o variabilă sau un argument independent. Variabila y a variabilei dependente, precum și valorile funcției. Scrieți funcția după cum urmează: y = f (x) ("jucătorul este egal cu EF de la X"). Simbolul f (x) indică, de asemenea, valoarea funcției cu argumentul x. f este regula prin care y depinde de x. În loc de f, se folosesc alte litere: g, φ și așa mai departe.
Exemplu 1 Editați

Când măsurați temperatura (a corpului), înălțimea la care mercurul va crește în termometru va depinde de temperatura corpului. De exemplu, dacă x este temperatura corpului în grade Celsius și y este înălțimea la care mercurul va crește în milimetri, atunci puteți scrie dependența lui x de y ca y = f (x). Dacă 0.1 ° C corespunde cu 1 mm, atunci f (x) = 10 (x - 35) (adică y = 10 (x - 35)). Ghici, de ce este necesar să scadă 35?
Să vedem ce înălțime va crește mercurul la o temperatură a corpului de 36,6 ° C:
f (36,6) = 10 (36,6-35) = 16 6) = 10 (366-35) = 16> (mm)
Exemplu 2 Editați
Dependența lungimii șinei la temperatură.
Exemplu 3 Editați
Domeniul și domeniul de aplicare al funcției Editare
Domeniul definiției este setul tuturor valorilor argumentului (variabila x). Intervalul de valori este setul tuturor valorilor funcției (variabilă y).
Funcția y = f (x) este dată dacă domeniul de definiție este specificat și regula prin care valoarea funcției poate fi determinată din valoarea dată a argumentului x. Dacă nu este specificat domeniul de aplicare al definiției, atunci se consideră că intervalul argumentului este toate valorile argumentului pentru care f (x) are sens.
Exemplu 1 Editați
Exemplu cu același termometru. Intervalul funcției y = 10 (x - 35) este scara termometrului. De exemplu, de la 35 ° C la 42 ° C (adică intervalul închis [35; 42]). Intervalul de valori va fi de la 0 mm la 70 mm (adică [0; 70]). Funcția noastră este dată.
Exemplu 2 Editați
Să rezolvăm problema:
g (x) = x + 7 >>. Definiți domeniul de aplicare al definiției funcției.
soluţie:
Domeniul funcției este toate expresiile posibile g (x). Asta este, domeniul de definiție va fi toate valorile lui x pentru care radicandul este mai mare sau egal cu zero:
x + 7 ⩾ 0
x ⩾ - 7
Răspuns: x ⩾ - 7 sau x ∈ [- 7; + 1)>)>.
Editarea funcției grafice
Graficul unei funcții este setul tuturor punctelor planului coordonatelor ale căror abscise sunt egale cu valorile argumentului, iar ordonatele la valorile corespunzătoare ale funcției.
Cu programări ale unor funcții, le-ați întâlnit deja în clasele anterioare.
Exemplu 1. Graficul unei funcții liniare Editați
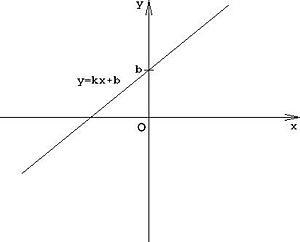
k și b sunt niște numere și k> 0.
Domeniul funcției este setul tuturor numerelor. Gama de valori pentru k ≠ 0 este setul tuturor numerelor, iar pentru k = 0, un număr b. Graficul unei funcții liniare este o linie dreaptă.
Exemplul 2. Graficul proporționalității inverse Editare
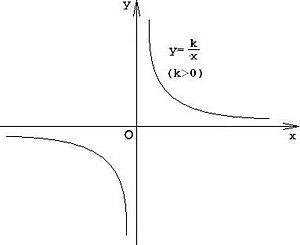
Domeniul funcției este setul de toate numerele, cu excepția zero. Graficul proporțional inversat este o hiperbolă.