Valori instantanee ale curentului sinusoidal, tensiunii, puterii. Conectarea secvențială și paralelă a elementelor
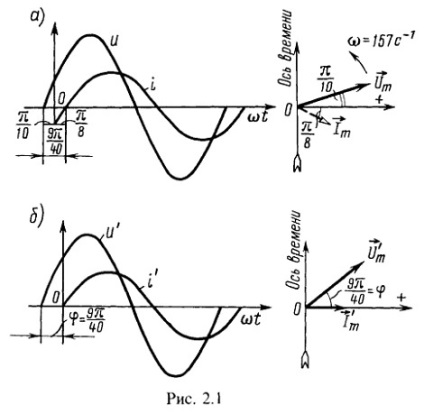
1. Construiește curbele schimbărilor de tensiune și curent în timp și trage vectorii care reprezintă funcțiile sinusoidale date:
Care este schimbarea de fază între tensiune și curent? Determinați perioada, frecvența, momentele de debut ale semnalelor de tensiune și curent pozitive. Ce fel de ecuații vor fi adoptate pentru tensiunea și curentul dat, dacă faza egală cu zero este luată pentru curent? În acest caz, construiți sinusoide de tensiune și curent, o diagramă vectorială.
soluţie:
Sinuzii u și i și vectorii corespunzători sunt arătați în Fig. 2.1, a.
Perioada.
frecvență.
Curentul de fază atinge tensiunea în unghi
Momentele de debut ale tensiunii și curentului semiautomate
Cu faza inițială a curentului egal cu zero, ecuațiile
pentru tensiune și curent va lua forma:
Curbele u ', i' și vectorii corespunzători sunt arătați în Fig. 2.1, b.
2. rezistive rezistență bobina R = 10 ohmi, inductanța L = 0,05 Gn este conectat la o sursă de tensiune sinusoidală, a cărei valoare efectivă U = 120B, iar frecvența f = 50 Hz. Determinați impedanța bobinei, curentului și fazei între tensiune și curent. Care sunt puterile active, reactive și depline?
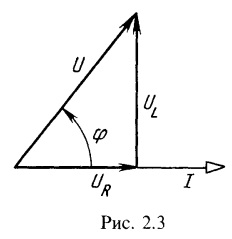
Calculați componentele active și reactive ale tensiunii la bornele bobinei. Care este emf-ul inductivității induse în bobină? Construiți o diagramă vectorică a tensiunilor și a curenților.

Diagrama vectorială este prezentată în Fig. 2.3
3. seria rpm conectat rezistor R = 120 ohmi și C = capacitatea condensatorului 30 este alimentat cu tensiunea uF u = 311sin314 t. V.
Calculați impedanța circuitului, valorile efective ale tensiunii și curentului, puterea consumată în stabilirea prețurilor, puterea reactivă și diferența de fază dintre tensiune și curent. Construiți o diagramă vectorică a tensiunilor și a curenților.
4. În concordanță cu un rezistor de rezistență. O bobină este inclusă, parametrii ei (figura 2.7, a). Se determină prețuri curente, diferența de fază între tensiune și curent și tensiune pe bobina reostat și defazajul între sursa de tensiune și de tensiune pe bobina dacă U = 220 V curent alternativ de frecvență f = 50 Hz. Calculați puterea activă, reactivă și plină a bobinei. Construiți o diagramă vectorială.
Curentul în circuit
Diferența de fază dintre tensiune și curent este determinată de exprimare
Tensiuni pe reostat și bobină:
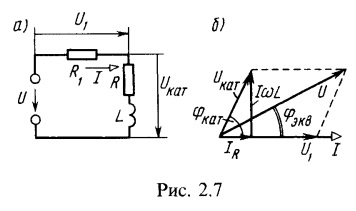
Defazajul între sursa de tensiune și tensiunea pe bobina exista ca diferența dintre unghiurile de fază (vezi diagrama vectorială din figura 2.7, b ..):
Bobine active, reactive și pline:
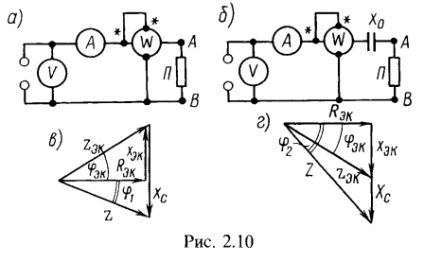
5. Pentru a determina parametrii circuitului echivalent din rețeaua pasivă cu două terminale AB (figura 2.10, a), tensiunile sunt măsurate. curent și putere. Pentru a determina natura reactanței echivalente a acestei rețele cu două terminale, un condensator a fost conectat în serie cu acesta (figura 2.10, b); în acest caz, cu aceeași tensiune aplicată, au arătat instrumentele. Frecvența curentului alternativ f = 50 Hz. Determinați parametrii circuitului echivalent al rețelei cu două terminale.
soluţie:
Parametrii circuitului echivalent al unei rețele cu două terminale, bazate pe datele inițiale (primul experiment)
Din datele celui de-al doilea experiment găsim
La o tensiune constantă conectată la circuit și o rezistență rezistivă constantă, curentul era mai mare decât curentul. Rezistența capacitivă suplimentară introdusă reduce rezistența totală a circuitului. Aceasta înseamnă că are un caracter inductiv. Valoare.
Valoarea necunoscută a rezistenței capacitive introduse adițional poate fi determinată în modul următor. Se stabilește că. Și din moment ce natura reacției totale este necunoscută în prealabil, atunci. Din datele celui de-al doilea experiment rezultă că. Din asta primim asta.
Menționăm că, pentru a determina natura reactanței echivalente a unei rețele cu două terminale, valoarea necunoscută a rezistenței capacitive introduse adițional ar trebui să fie mai mică. Acest lucru poate fi văzut din Fig. 2.10, c și d, pe care sunt reprezentate grafic diagrame de rezistență, corespunzând celui de-al doilea experiment. Pentru și pentru (Figura 2.10, c) și pentru (Figura 2.10, d). Dacă o luați. fiecare dintre unghiuri este mai mare.
Dacă valoarea rezistenței introduse suplimentar este cunoscută în prealabil, poate fi luată mai mult.
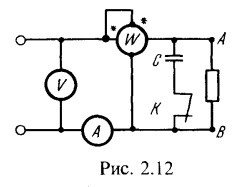
6. Dispozitivele conectate la rețeaua pasivă cu două terminale AB (în figura 2.12, contactul K deschis), au arătat. Pentru a determina natura reactanței rețelei cu două terminale, un condensator (contactul K închis) a fost conectat în paralel, rezistența sa capacitivă. în timp ce instrumentele au arătat :. Determinați parametrii echivalenți ai rețelei cu două terminale.
soluţie:
Rezistența unui circuit de serie al unei rețele cu două terminale:
Parametrii circuitului său paralel sunt:
Conductivitatea condensatorului.
Parametrii unui circuit echivalent constând dintr-o rețea cu două terminale și un condensator:
Deci, cum. atunci reactanța unui cercetător al unei rețele cu două terminale este de natură capacitivă. Același rezultat rezultă din următoarea întâlnire. Deoarece la aceeași tensiune, curentul după conectarea condensatorului a devenit mai lung decât înainte de conectare, conductivitatea totală a circuitului a crescut. Acesta poate fi cazul în care filiala conectabile susceptance are același caracter ca țintă susceptance de două terminale, cu condiția.
7. Pentru a determina parametrii unui condensator cu pierderi, acesta a fost conectat la o sursă de tensiune sinusoidală U = 19,5 V (f = 50 kHz). În acest caz, ampermetrul a arătat un curent I = 0,3 A și un contor de putere P = 153 mW. Determinați cele două scheme din Fig. 2.17, a și b, echivalent cu un condensator cu pierderi. Care este tangenta unghiului de pierdere al acestui condensator si factorul Q?
soluţie:
Definiți schimbarea de fază între tensiunea U și curentul I.
Semnul este negativ, deoarece circuitul constă în rezistență rezistivă și capacitate.
Din circuitul din Fig. 2.17, dar este clar că.
Să găsim componenta activă a curentului