Algoritmul de calcul al celui mai mare divizor comun (GCD) a fost descoperit de matematicienii greci antic și este cunoscut sub numele de algoritmul "scădere reciprocă". Și, deși menționarea acestui algoritm este încă în Aristotel, mai târziu a fost numit algoritmul euclidian. Care este cel mai mare divizor comun, proprietățile sale și metodele computationale sunt luate în considerare în [1].
Amintiți-vă că GCD a două numere poate fi calculată în funcție de următoarea reapariție:
În limba C, procedura de calcul al GCD este:
int gcd (int a, int b)
dacă (b == 0) returnați a;
retur gcd (b, a% b);
Algoritmul euclidian poate fi extins pentru a găsi numere întregi x și y date a și b. acea axă + de = d. unde d este cel mai mare divizor comun al a și b.
Apoi, valorile lui x și y. care sunt soluții ale ecuației ax + by = d. sunt găsite de la
x = y ', y = x' - y '(2)
Întreaga parte a a / b este notată aici.
Dovada. Deoarece un mod b = a - · b.
d = x '· b + y' · (a - · b) = y '· a + (x' - y '
unde x = y ', y = x' - y 'este notat.
Funcția gcdext (int a. int b. int * d. int * x. int * y), de mai jos, de la numerele de intrare a și b este d = cmmdc (a. b) și astfel x. y astfel încât d = a · x + b · y. Pentru a căuta x și y necunoscute, executați recursiv gcdext (b. A mod b. D. X. Y) și recalculați valorile x și y din formula de mai sus. Recursivitatea se termină când b = 0. Dacă b = 0 cmmdc (a. 0) = a și a = a · 1 + 0 · 0, deci presupunem x = 1, y = 0.
void gcdext (int a, int b, int * d, int * x, int * y)
Pentru o execuție manuală a algoritmului Euclidian extins, este convenabil să se utilizeze un tabel cu patru coloane (după cum se arată în exemplul de mai jos) care corespunde valorilor lui a. b. x. y. Împărțim procesul de calcul în trei etape:
a) Mai întâi, vom calcula GCD (a. b) utilizând primele două coloane ale tabelului și relației (1). Ultimul rând din coloana (a) va conține valoarea d = GCD (a. B).
b) Introduceți valorile 1 și respectiv 0 în coloanele x și y ale ultimei linii.
c) Vom completa rândurile succesive pentru coloanele x și y de jos în sus. Valorile lui x și y din ultima linie sunt deja introduse în etapa b). Presupunând că linia curentă sunt deja umplute valori (x „y“), folosim formula (2) va recalcula și scrie valori (x. Y) în linia celulară corespunzătoare în picioare deasupra.
1. Algoritmul avansat al lui Euclid. Să găsim soluția ecuației 5x + 3y = 1. Calculați GCD (5, 3) și găsiți numărul x corespunzător. y producem în tabel:
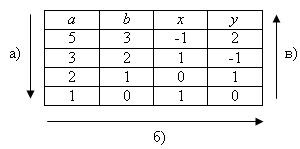
Ordinea și direcția calculelor sunt indicate prin săgeți și litere.
Din tabel, constatăm că GCD (5, 3) = 5 · (-1) + 3 · 2 = 1, adică x = -1, y = 2.
Să luăm în considerare, de exemplu, cum s-au obținut valorile (x, Y) pentru primul rând. Din a doua linie luăm valorile (x ', y') = (1, -1). Prin formulele (2) obținem:
y = x '- y' '= 1 - (-1) - = 1 + 1 = 2
O comparație liniară este o ecuație a formei ax = b (mod n). Ea are o soluție dacă și numai dacă b este divizibilă de d = GCD (a. N). Daca d> 1, atunci ecuatia poate fi simplificata prin inlocuirea acesteia cu 'x = b' (mod n '), unde a' = a / d. b '= b / d. n '= n / d. După o astfel de transformare, numerele a 'și n' sunt relativ prime.
Algoritmul de rezolvare a ecuației a 'x = b' (mod n ') cu relativ prime a' și n 'constă din două părți:
1. Rezolvați ecuația a 'x = 1 (mod n'). Pentru a face acest lucru, folosind algoritmul lui Euclid extins caute (x0. Y0) ecuație soluția unei 'x + n' y = 1. Luând modulo n 'ultima egalitate obținem o' x0 = 1 (mod n „).
Un exemplu. Rezolva ecuația 18x = 6 (mod 8).
Valoarea d = GCD (18, 8) = 2 este un divizor de 6, deci soluția există. După simplificare, obținem ecuația 9x = 3 (mod 4). Aceasta, prin lemma, este echivalent cu 3x = 1 (mod 4). Rezolvarea 3x ecuație + 4y = 1 folosind algoritmul lui Euclid extins, obținem x = -1, y = 1. În cazul în care x = -1 (mod 4) = 3. Aceasta înseamnă că x = 3 va fi ca o soluție de 3x = 1 (mod 4 ) și 18x = 6 (mod 8).
Ecuații eco-eficace ale formei
În această secțiune considerăm algoritmul pentru găsirea de soluții ale ecuației Diophantine liniare cu două necunoscute de forma a · x + b · y = c (în continuare, pentru simplitate, vom omite semnele de multiplicare și scriere proto ax + de = c).
Teorema 1. Ecuația ax + by = c are o soluție în întregi dacă și numai dacă c este divizibilă prin GCD (a. B).
Teoremă 2. Dacă perechea (x0, y0) este o soluție a axei de ecuație + de = c. atunci întregul set al soluțiilor sale (x, y) este descris de formula:
Pentru a găsi soluțiile parțiale ecuației ax + prin = c trebuie să găsească o soluție (x „y“) toporului ecuației + prin = d (d - cmmdc a și b) (X0 y0.) Folosind algoritmul lui Euclid extins, după înmulțiți-l cu c / d. Asta este
Un exemplu. Găsiți setul de soluții al ecuației Sx + 3y = 7.
1. Ecuația are o soluție, deoarece 7 este divizibilă de GCD (5, 3) = 1.
2. Găsiți soluția ecuației 5x '+ 3y' = 1 folosind algoritmul extins euclidian: (x ', y') = (-1, 2).
3. Gasim solutia (x0, y0) a ecuatiei originale Diophantine:
Conform teoremei 2, setul de soluții al ecuației Diophantine originale are forma: