Prezentare pe tema: "Mișcări: mapările unui spațiu în sine care păstrează distanța dintre puncte sunt numite mișcările spațiului: mapările spațiului în sine" - Transcriere:
2 Cartografierea spațiului pe sine, păstrând distanța dintre puncte, se numește mișcări de spațiu. Amplasarea unui spațiu în sine, care păstrează distanța dintre puncte, se numește mișcări de spațiu. Astfel, dacă în mișcarea spațiului punctele A și B trec (sunt mapate) la punctele A 1 și B 1, Astfel, dacă spațiul A și B se deplasează (sunt mapate) la punctele A 1 și B 1 atunci când se deplasează spațiul, atunci AB = A 1 B 1. atunci AB = A 1 B 1.

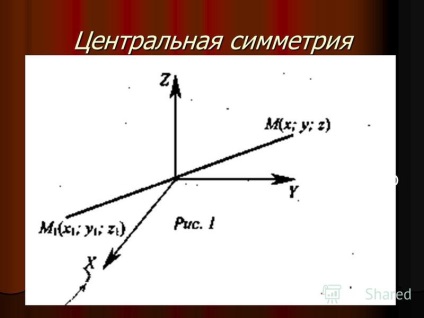
3 Exemplul 1. Simetria centrală a mișcării poate fi simetrie centrală - spațiul de afișare în care orice punct M s devine simetric cu punctul A 1 al centrului O. 1. Un exemplu de mișcare poate fi simetrie centrală - spațiul de afișare, în care orice punct M trece în punctul A 1 simetric față de acesta în raport cu centrul dat O.
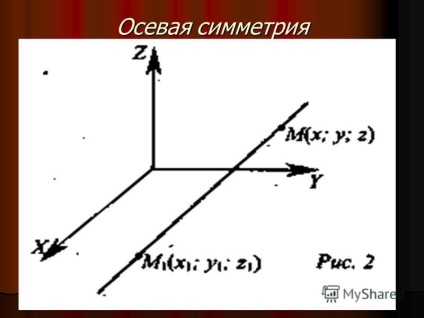
4 Simetrie axială Simetria axială cu axa a este o cartografiere a spațiului pe el însuși astfel încât orice punct M să treacă în punctul M1 simetric față de el față de axa a. Simetria axială cu axa a este o cartografiere a spațiului pe ea însăși astfel încât orice punct M să treacă în punctul M1 simetric față de el în raport cu axa a.
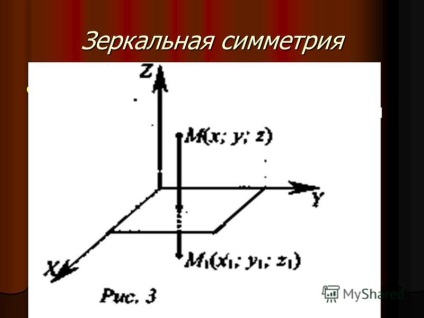
5 simetrie în oglindă a simetriei oglinzii (simetrie în raport cu un plan) este o harta pe sine, în care orice punct M e devine simetric față de un plan și punctul M 1. simetrie în oglindă (simetrie în raport cu un plan) este o hartă pe sine, cu unde orice punct M trece în punctul M 1 simetric față de planul a.
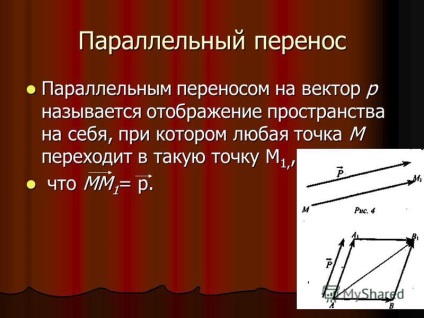
6 transferul paralel în paralel a transferului de către vectorul p se numește cartarea pe sine, prin care orice punct M se duce la un transfer punct M 1 paralel cu vectorul p este o hartă pe sine astfel încât orice punct M merge la un punct care 1. M MM 1 = p. că MM = p.
7
